Magnetic moment
| Electromagnetism | ||||||||||||
 |
||||||||||||
Electricity · Magnetism
|
||||||||||||
In physics, astronomy, chemistry, and electrical engineering, the term magnetic moment of a system (such as a loop of electric current, a bar magnet, an electron, a molecule, or a planet) usually refers to its magnetic dipole moment, and is a measure of the strength of the system's net magnetic source. Specifically, magnetic dipole moment quantifies the contribution of the system's internal magnetism to the external dipolar magnetic field produced by the system (i.e. the component of the external magnetic field that drops off with distance as the inverse cube). Any dipolar magnetic field pattern is symmetric with respect to rotations around a particular axis, therefore it is customary to describe the magnetic dipole moment that creates such a field as a vector with a direction along that axis. For quadrupolar, octupolar, and higher-order multipole magnetic moments, see Multipole expansion.
Two kinds of magnetic sources
Fundamentally, contributions to any system's magnetic moment may come from sources of two kinds: (1) motion of electric charges, such as electric currents and (2) the intrinsic magnetism of elementary particles, such as the electron.
Contributions due to the sources of the first kind can be calculated from knowing the distribution of all the electric currents (or, alternatively, of all the electric charges and their velocities) inside the system, by using the formulas below. On the other hand, the magnitude of each elementary particle's intrinsic magnetic moment is a fixed number, often measured experimentally to a great precision. For example, any electron's magnetic moment is measured to be −9.284764×10-24 J/T.[1] The direction of the magnetic moment of any elementary particle is entirely determined by the direction of its spin (the minus in front of the value above indicates that any electron's magnetic moment is antiparallel to its spin).
Finally, the net magnetic moment of any system is a vector sum of contributions from one or both types of sources. For example, a hydrogen atom's magnetic moment is a vector sum of the following contributions: the intrinsic moment of the electron, the orbital motion of the electron around the proton, and the intrinsic moment of the proton.
Examples of magnetic moments
Magnetic moment of electrons
Electrons and many nuclei also have intrinsic magnetic moments, an explanation of which requires a quantum mechanical treatment and relates to the intrinsic angular momentum of the particles as discussed in the article electron magnetic dipole moment. It is these intrinsic magnetic moments that give rise to the macroscopic effects of magnetism, and other phenomena, such as nuclear magnetic resonance.
The magnetic moment of the electron is
where
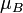 is the Bohr Magneton,
is the Bohr Magneton,
and
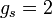 in Dirac mechanics, but is slightly larger due to quantum electrodynamics effects.
in Dirac mechanics, but is slightly larger due to quantum electrodynamics effects.
Again it is important to notice that 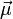 is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum. This can be understood with the following classical picture: if we imagine that the spin angular momentum is created by the electron mass spinning around some axis, the electric current that this rotation creates spins in the opposite direction, because of the negative charge of the electron; such current loops produce a magnetic moment which is antiparallel to the spin angular momentum.
is a negative constant multiplied by the spin, so the magnetic moment is antiparallel to the spin angular momentum. This can be understood with the following classical picture: if we imagine that the spin angular momentum is created by the electron mass spinning around some axis, the electric current that this rotation creates spins in the opposite direction, because of the negative charge of the electron; such current loops produce a magnetic moment which is antiparallel to the spin angular momentum.
Magnetic moments of nuclei
- Also see nuclear magnetic moment.
The nuclear system is a complex physical system consisting of nucleons, i.e., protons and neutrons. The quantum mechanical properties of the nucleons include the spin among others. Since the electromagnetic moments of the nucleus depends on the spin of the individual nucleons, one can look at these properties with measurements of nuclear moments, and more specifically the nuclear magnetic dipole moment.
The nuclear magnetic moment is very sensitive to the individual contributions from nucleons and a measurement or prediction of its value can reveal important information about the content of the nuclear wavefunction. There are several theoretical models that predict the value of the magnetic dipole moment and a number of experimental techniques aiming to carry out measurements in nuclei along the nuclear chart.
Magnetic moments of molecules
Any molecule has a well-defined magnitude of magnetic moment, which may depend on the molecule's energy state. Typically, the overall magnetic moment of a molecule is a combination of the following contributions, in the order of their typical strength:
- magnetic moments due to its unpaired electron spins (paramagnetic contribution), if any
- orbital motion of its electrons, which in the ground state is often proportional to the external magnetic field (diamagnetic contribution)
- the combined magnetic moment of its nuclear spins, which depends on the nuclear spin configuration.
Examples of molecular magnetism
- Oxygen molecule, O2, exhibits strong paramagnetism, due to unpaired spins of its outermost two electrons.
- Carbon dioxide molecule, CO2, mostly exhibits diamagnetism, a much weaker magnetic moment of the electron orbitals that is proportional to the external magnetic field. In the rare instance when a magnetic isotope, such as 13C or 17O, is present, it will contribute its nuclear magnetism to the molecule's magnetic moment.
- Hydrogen molecule, H2, in a weak (or zero) magnetic field exhibits nuclear magnetism, and can be in a para- or an ortho- nuclear spin configuration.
Formulas and values for calculating magnetic moments
In the simplest case of a planar loop of electric current, its magnetic moment is defined as:
where
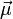 is the magnetic moment, a vector measured in ampere–square meters, or equivalently in joules per tesla,
is the magnetic moment, a vector measured in ampere–square meters, or equivalently in joules per tesla,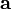 is the vector area of the current loop, measured in square meters (x, y, and z coordinates of this vector are the areas of projections of the loop onto the yz, zx, and xy planes), and
is the vector area of the current loop, measured in square meters (x, y, and z coordinates of this vector are the areas of projections of the loop onto the yz, zx, and xy planes), and is the current in the loop (assumed to be constant), a scalar measured in amperes.
is the current in the loop (assumed to be constant), a scalar measured in amperes.
By convention, the direction of the vector area is given by the right hand grip rule (curling the fingers of one's right hand in the direction of the current around the loop, when the palm of the hand is "touching" the loop's outer edge, and the straight thumb indicates the direction of the vector area and thus of the magnetic moment).
In case of an arbitrary closed loop of constant current 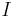 , the magnetic moment is given by
, the magnetic moment is given by
where 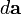 is the element of the vector area of the current loop.
is the element of the vector area of the current loop.
In the most general case of an arbitrary current distribution in space, the magnetic moment of such a distribution can be found from the following equation:
where
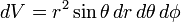 is the volume element,
is the volume element, 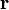 is the position vector pointing from the origin to the location of the volume element, and J is the current density vector at that location.
is the position vector pointing from the origin to the location of the volume element, and J is the current density vector at that location.
The above equation can be used for calculating a magnetic moment of any assembly of moving charges, such as a spinning charged solid, by substituting
 where
where 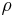 is the electric charge density at a given point and
is the electric charge density at a given point and 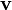 is the instantaneous linear velocity of that point.
is the instantaneous linear velocity of that point.
For example, the magnetic moment produced by an electric charge moving along a circular path is
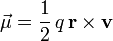 ,
,
where 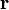 is the position of the charge
is the position of the charge 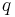 relative to the center of the circle and
relative to the center of the circle and 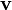 is the instantaneous velocity of the charge.
is the instantaneous velocity of the charge.
For a free point charge moving in an external magnetic field the magnetic moment is a measure of the magnetic flux set up by the gyration of the charge in the magnetic field. The moment is opposite to the direction of magnetic field (i.e. it is diamagnetic) and is equal to the kinetic energy of the rotary motion divided by the magnetic field.
For a spinning charged solid with a uniform charge density to mass density ratio, the ratio of its magnetic moment to its angular momentum, also known as gyromagnetic ratio, is equal to half the charge-to-mass ratio. This implies that a more massive assembly of charges spinning with the same angular momentum will have a proportionately weaker magnetic moment, compared to its lighter counterpart. Even though atomic particles cannot be accurately described as spinning charge distributions of uniform charge-to-mass ratio, this general trend can be sometimes observed in the atomic world, where intrinsic angular momenta of most particles are fairly constant: a small half-integer (spin) times the reduced Planck constant 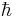 . This is the basis for defining the magnetic moment units of Bohr magneton (assuming charge-to-mass ratio of the electron) and nuclear magneton (assuming charge-to-mass ratio of the proton).
. This is the basis for defining the magnetic moment units of Bohr magneton (assuming charge-to-mass ratio of the electron) and nuclear magneton (assuming charge-to-mass ratio of the proton).
In atomic and nuclear physics, the symbol 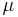 represents the magnitude of the magnetic moment, often measured in Bohr magnetons or nuclear magnetons, associated with the intrinsic spin of the particle and/or with the orbital motion of the particle in a system. Values of the intrinsic magnetic moments of some particles are given in the table below:
represents the magnitude of the magnetic moment, often measured in Bohr magnetons or nuclear magnetons, associated with the intrinsic spin of the particle and/or with the orbital motion of the particle in a system. Values of the intrinsic magnetic moments of some particles are given in the table below:
| Particle | Magnetic dipole moment in SI units, 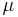 (10-27 J/T) (10-27 J/T) |
Spin (dimensionless) |
|---|---|---|
| electron | -9284.764 | 1/2 |
| proton | +14.106067 | 1/2 |
| neutron | -9.66236 | 1/2 |
| muon | -44.904478 | 1/2 |
| deuteron | +4.3307346 | 1 |
| triton | +15.046094 | 1/2 |
For relation between the notions of magnetic moment and magnetization see magnetization.
Magnetic field produced by a magnetic moment
Any system possessing a net magnetic dipole moment 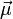 will produce a dipolar magnetic field (described below) in the space surrounding the system. While the net magnetic field produced by the system can also have higher-order multipole components, those will drop off with distance more rapidly, so that only the dipolar component will dominate the magnetic field of the system at distances far away from it.
will produce a dipolar magnetic field (described below) in the space surrounding the system. While the net magnetic field produced by the system can also have higher-order multipole components, those will drop off with distance more rapidly, so that only the dipolar component will dominate the magnetic field of the system at distances far away from it.
Choosing a frame of reference in which the system center is at the origin, and the z axis is pointing in the direction of the system's magnetic moment 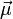 simplifies the description of the magnetic field. In such frame of reference, the components of the dipolar magnetic field produced by the system, at any point (x,y,z) in space, are (in teslas):
simplifies the description of the magnetic field. In such frame of reference, the components of the dipolar magnetic field produced by the system, at any point (x,y,z) in space, are (in teslas):

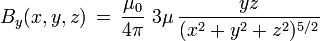
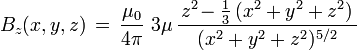 , as well as the 'transverse' component:
, as well as the 'transverse' component:
- where
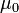 is the magnetic constant,
is the magnetic constant,  is the number Pi,
is the number Pi, 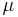 is the magnitude of
is the magnitude of 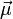 , and x, y, and z are coordinates measured in metres.
, and x, y, and z are coordinates measured in metres.
Effects of an external magnetic field on a magnetic moment
Equivalently, the magnetic moment of an object can be defined as a vector relating the aligning torque on the object from an externally applied magnetic field to the field vector itself. The relationship is given by
where
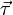 is the torque, measured in newton-meters,
is the torque, measured in newton-meters,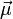 is the magnetic moment, measured in ampere meters-squared, and
is the magnetic moment, measured in ampere meters-squared, and is the magnetic field, measured in teslas or, equivalently in newtons per (ampere-meter).
is the magnetic field, measured in teslas or, equivalently in newtons per (ampere-meter).
A magnetic moment in an externally-produced magnetic field has a potential energy U:
In a case when the external magnetic field is non-uniform, there will be a force, proportional to the magnetic field gradient, acting on the magnetic moment itself. There have been some discussion on how to calculate the force acting on a magnetic dipole. There are two expressions for the force acting on a magnetic dipole. The expression varies depending on the model used for the dipole [3], i.e. a current loop or two monopoles (analogous to the electric dipole). The force obtained in the case of a current loop model is
In the case a pair of monopoles are used (i.e. electric dipole model)
and one can be put in terms of the other via the relation
In all these expressions  is the dipole and
is the dipole and 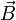 is the magnetic field at its position.
is the magnetic field at its position.
Forces between two magnetic dipoles
If 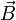 in the previous equations is replaced with the expression of the field of a magnetic dipole under the approximation for distances bigger than the characteristic length of the dipole [4]. Namely,
in the previous equations is replaced with the expression of the field of a magnetic dipole under the approximation for distances bigger than the characteristic length of the dipole [4]. Namely,

where the variables  and
and 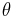 are measured in a frame of reference with origin in
are measured in a frame of reference with origin in 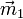 and oriented in such a way that
and oriented in such a way that 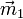 lies in the x-axis. This frame is called Local coordinates and is shown in the Figure on the right.
lies in the x-axis. This frame is called Local coordinates and is shown in the Figure on the right.
The final formulas are shown next. They are expressed in the global coordinate system,
The torque is straightforward to obtain from the formula
which gives
Magnetic poles, analogy with the electric dipole moment
Magnetic moment can be visualized as a bar magnet which has magnetic poles of equal magnitude but opposite polarity. Each pole is the source of magnetic force which weakens with distance. Since magnetic poles always come in pairs, their forces partially cancel each other because while one pole pulls, the other repels. This cancellation is greatest when the poles are close to each other i.e. when the bar magnet is short. The magnetic force produced by a bar magnet, at a given point in space, therefore depends on two factors: on both the strength p of its poles, and on the distance d separating them. The force is proportional to the product 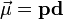 , where
, where 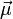 describes the "magnetic moment" or "dipole moment" of the magnet along a distance R and its direction as the angle between R and the axis of the bar magnet. These equations are completely analogous to the case of electric dipole moment.
describes the "magnetic moment" or "dipole moment" of the magnet along a distance R and its direction as the angle between R and the axis of the bar magnet. These equations are completely analogous to the case of electric dipole moment.
See also
- Magnetic dipole models
- Dipole
- Electric dipole moment
- Magnetization
- Magnetic dipole-dipole interaction
Notes
- ↑ NIST μe
- ↑ See NIST's Fundamental Physical Constants website http://physics.nist.gov/cgi-bin/cuu/Results?search_for=+magnetic+moment
- ↑ Timothy H. Boyer (1988). The force on a magnetic dipole.American Journal of Physics 56(8), pp. 688-692,doi 10.1119/1.15501
- ↑ Schill, R.A., Jr. (2003). General relation for the vector magnetic field of a circular current loop: a closer look. Magnetics, IEEE Transactions on Volume 39, Issue 2, pp.961 - 967.
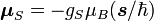
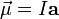
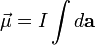
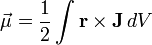

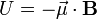
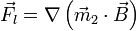
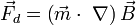
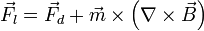
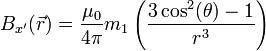
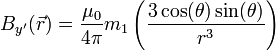
![F_r(\vec{r}, \alpha, \beta) = - \frac{3 \mu_0}{4 \pi}\frac{m_2 m_1}{r^4}\left[2\cos(\phi - \alpha)\cos(\phi - \beta)- \sin(\phi - \alpha)\sin(\phi - \beta)\right]](/2009-wikipedia_en_wp1-0.7_2009-05/I/9bc69956304c7544a0297da0bb804379.png)
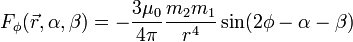
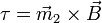
![\tau = \frac{\mu_0}{4 \pi}\frac{m_1 m_2}{r^3}\left[3\cos(\phi-\alpha)\sin(\phi-\beta)+\sin(\beta-\alpha)\right]](/2009-wikipedia_en_wp1-0.7_2009-05/I/6880781e851e5cbb679f2d85896e25d1.png)