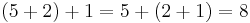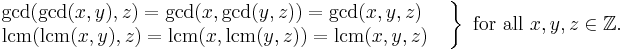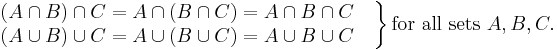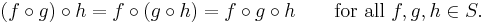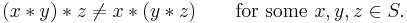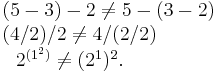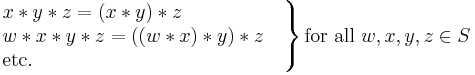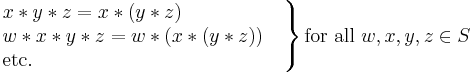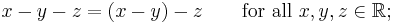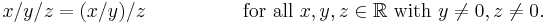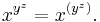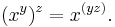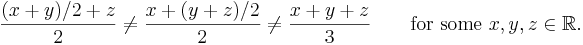Associativity

In mathematics, associativity is a property that a binary operation can have. It means that, within an expression containing two or more of the same associative operators in a row, the order that the operations are performed does not matter as long as the sequence of the operands is not changed. That is, rearranging the parentheses in such an expression will not change its value. Consider for instance the equation

$(5+2)+1=5+(2+1)=8 \,$

Even though the parentheses were rearranged (the left side requires adding 5 and 2 first, then adding 1 to the result, whereas the right side requires adding 2 and 1 first, then 5), the value of the expression was not altered. Since this holds true when performing addition on any real numbers, we say that "addition of real numbers is an associative operation."

Associativity is not to be confused with commutativity. Commutativity justifies changing the order or sequence of the operands within an expression while associativity does not. For example,

$(5+2)+1=5+(2+1) \,$

is an example of associativity because the parentheses were changed (and consequently the order of operations during evaluation) while the operands 5, 2, and 1 appeared in the exact same order from left to right in the expression.

$(5+2)+1=(2+5)+1 \,$

is not an example of associativity because the operand sequence changed when the 2 and 5 switched places.

Associative operations are abundant in mathematics, and in fact most algebraic structures explicitly require their binary operations to be associative. However, many important and interesting operations are non-associative; one common example would be the vector cross product.

1 Definition
2 Examples
3 Non-associativity
4 More examples
5 See also

Definition

Formally, a binary operation $*\!\!\!$ on a set S is called associative if it satisfies the associative law:

$(x * y) * z=x * (y * z)\qquad\mbox{for all }x,y,z\in S.$

Using * to denote a binary operation performed on a set

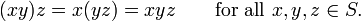
$(xy)z=x(yz) = xyz \qquad\mbox{for all }x,y,z\in S.$

An example of multiplicative associativity

The evaluation order does not affect the value of such expressions, and it can be shown that the same holds for expressions containing any number of $*\!\!\!$ operations. Thus, when $*\!\!\!$ is associative, the evaluation order can therefore be left unspecified without causing ambiguity, by omitting the parentheses and writing simply:

$xyz,$

However, it is important to remember that changing the order of operations does not involve or permit changing the actual operations themselves by moving the operands around within the expression.

Examples

Some examples of associative operations include the following.

In arithmetic, addition and multiplication of real numbers are associative; i.e.,

$\left. \begin{matrix} (x+y)+z=x+(y+z)=x+y+z\quad \\ (x\,y)z=x(y\,z)=x\,y\,z\qquad\qquad\qquad\quad\ \ \, \end{matrix} \right\} \mbox{for all }x,y,z\in\mathbb{R}.$

Addition and multiplication of complex numbers and quaternions is associative. Addition of octonions is also associative, but multiplication of octonions is non-associative.

The greatest common divisor and least common multiple functions act associatively.

$\left. \begin{matrix} \operatorname{gcd}(\operatorname{gcd}(x,y),z)= \operatorname{gcd}(x,\operatorname{gcd}(y,z))= \operatorname{gcd}(x,y,z)\ \quad \\ \operatorname{lcm}(\operatorname{lcm}(x,y),z)= \operatorname{lcm}(x,\operatorname{lcm}(y,z))= \operatorname{lcm}(x,y,z)\quad \end{matrix} \right\}\mbox{ for all }x,y,z\in\mathbb{Z}.$

Because linear transformations are functions that can be represented by matrices with matrix multiplication being the representation of functional composition, one can immediately conclude that matrix multiplication is associative.

Taking the intersection or the union of sets:

$\left. \begin{matrix} (A\cap B)\cap C=A\cap(B\cap C)=A\cap B\cap C\quad \\ (A\cup B)\cup C=A\cup(B\cup C)=A\cup B\cup C\quad \end{matrix} \right\}\mbox{for all sets }A,B,C.$

If M is some set and S denotes the set of all functions from M to M, then the operation of functional composition on S is associative:

$(f\circ g)\circ h=f\circ(g\circ h)=f\circ g\circ h\qquad\mbox{for all }f,g,h\in S.$

Slightly more generally, given four sets M, N, P and Q, with h: M to N, g: N to P, and f: P to Q, then

$(f\circ g)\circ h=f\circ(g\circ h)=f\circ g\circ h$

as before. In short, composition of maps is always associative.

Consider a set with three elements, A, B, and C. The following operation:

×	A	B	C
+
A	A	A	A
B	A	B	C
C	A	A	A

is associative. Thus, for example, A(BC)=(AB)C. This mapping is not commutative.

Non-associativity

A binary operation $*$ on a set S that does not satisfy the associative law is called non-associative. Symbolically,

$(x*y)*z\ne x*(y*z)\qquad\mbox{for some }x,y,z\in S.$

For such an operation the order of evaluation does matter. Subtraction, division and exponentiation are well-known examples of non-associative operations:

$\begin{matrix} (5-3)-2\ne 5-(3-2)\quad \\ (4/2)/2\ne 4/(2/2)\qquad\qquad \\ 2^{(1^2)}\ne (2^1)^2.\quad\qquad\qquad \end{matrix}$

In general, parentheses must be used to indicate the order of evaluation if a non-associative operation appears more than once in an expression. However, mathematicians agree on a particular order of evaluation for several common non-associative operations. This is simply a syntactical convention to avoid parentheses.

A left-associative operation is a non-associative operation that is conventionally evaluated from left to right, i.e.,

$\left. \begin{matrix} x*y*z=(x*y)*z\qquad\qquad\quad\, \\ w*x*y*z=((w*x)*y)*z\quad \\ \mbox{etc.}\qquad\qquad\qquad\qquad\qquad\qquad\ \ \, \end{matrix} \right\} \mbox{for all }w,x,y,z\in S$

while a right-associative operation is conventionally evaluated from right to left:

$\left. \begin{matrix} x*y*z=x*(y*z)\qquad\qquad\quad\, \\ w*x*y*z=w*(x*(y*z))\quad \\ \mbox{etc.}\qquad\qquad\qquad\qquad\qquad\qquad\ \ \, \end{matrix} \right\} \mbox{for all }w,x,y,z\in S$

Both left-associative and right-associative operations occur; examples are given below.

More examples

Left-associative operations include the following.

Subtraction and division of real numbers:

$x-y-z=(x-y)-z\qquad\mbox{for all }x,y,z\in\mathbb{R};$

$x/y/z=(x/y)/z\qquad\qquad\quad\mbox{for all }x,y,z\in\mathbb{R}\mbox{ with }y\ne0,z\ne0.$

Right-associative operations include the following.

Exponentiation of real numbers:

$x^{y^z}=x^{(y^z)}.\,$

The reason exponentiation is right-associative is that a repeated left-associative exponentiation operation would be less useful. Multiple appearances could (and would) be rewritten with multiplication:

$(x^y)^z=x^{(yz)}.\,$

Non-associative operations for which no conventional evaluation order is defined include the following.

Taking the pairwise average of real numbers:

${(x+y)/2+z\over2}\ne{x+(y+z)/2\over2}\ne{x+y+z\over3}\qquad\mbox{for some }x,y,z\in\mathbb{R}.$

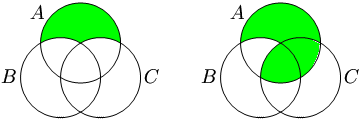
Taking the relative complement of sets:

$(A\backslash B)\backslash C\ne A\backslash (B\backslash C)\qquad\mbox{for some sets }A,B,C.$

$Venn diagram of the relative complements (A\B)\C and A\(B\C)$

The green part in the left Venn diagram represents $(A\backslash B)\backslash C$ . The green part in the right Venn diagram represents $A\backslash(B\backslash C)$ .

Using right-associative notation for material conditional can be motivated e.g. by Curry-Howard correspondence: see e.g. comparison of the first two axioms of the Hilbert-style deduction system with basic combinators of combinatory logic.

Associativity

Contents

Definition

Examples

Non-associativity

More examples

See also