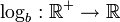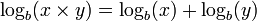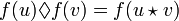Isomorphism

In abstract algebra, an isomorphism (Greek: ἴσος isos "equal", and μορφή morphe "shape") is a bijective map f such that both f and its inverse f⁻¹ are homomorphisms, i.e., structure-preserving mappings.

In the more general setting of category theory, an isomorphism is a morphism f:X→Y in a category for which there exists an "inverse" f⁻¹:Y→X, with the property that both f⁻¹f=id_X and ff⁻¹=id_Y.

Informally, an isomorphism is a kind of mapping between objects, which shows a relationship between two properties or operations. If there exists an isomorphism between two structures, we call the two structures isomorphic. In a certain sense, isomorphic structures are structurally identical, if you choose to ignore finer-grained differences that may arise from how they are defined.

1 Purpose
2 Practical example
3 Abstract examples
- 3.1 A relation-preserving isomorphism
- 3.2 An operation-preserving isomorphism
4 Applications
5 See also
6 External links

Purpose

Isomorphisms are studied in mathematics in order to extend insights from one phenomenon to others: if two objects are isomorphic, then any property which is preserved by an isomorphism and which is true of one of the objects is also true of the other. If an isomorphism can be found from a relatively unknown part of mathematics into some well studied division of mathematics, where many theorems are already proved, and many methods are already available to find answers, then the function can be used to map whole problems out of unfamiliar territory over to "solid ground" where the problem is easier to understand and work with.

Practical example

The following are examples of isomorphisms from ordinary algebra.

Consider the logarithm function: For any fixed base b, the logarithm function log_b maps from the positive real numbers 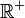$\mathbb{R}^+$ onto the real numbers 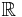$\mathbb{R}$ ; formally:

$\log_b�: \mathbb{R}^+ \to \mathbb{R} \!$

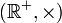This mapping is one-to-one and onto, that is, it is a bijection from the domain to the codomain of the logarithm function. In addition to being an isomorphism of sets, the logarithm function also preserves certain operations. Specifically, consider the group $(\mathbb{R}^+,\times)$ of positive real numbers under ordinary multiplication. The logarithm function obeys the following identity:

$\log_b(x \times y) = \log_b(x) + \log_b(y) \!$

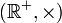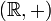But the real numbers under addition also form a group. So the logarithm function is in fact a group isomorphism from the group $(\mathbb{R}^+,\times)$ to the group $(\mathbb{R},+)$ .
Logarithms can therefore be used to simplify multiplication of real numbers. By working with logarithms, multiplication of positive real numbers is replaced by addition of logs. This way it is possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale.
Consider the group Z₆, the numbers from 0 to 5 with addition modulo 6. Also consider the group Z₂ × Z₃, the ordered pairs where the x coordinates can be 0 or 1, and the y coordinates can be 0, 1, or 2, where addition in the x-coordinate is modulo 2 and addition in the y-coordinate is modulo 3. These structures are isomorphic under addition, if you identify them using the following scheme:

(0,0) -> 0

(1,1) -> 1

(0,2) -> 2

(1,0) -> 3

(0,1) -> 4

(1,2) -> 5

or in general (a,b) -> ( 3a + 4 b ) mod 6. For example note that (1,1) + (1,0) = (0,1) which translates in the other system as 1 + 3 = 4. Even though these two groups "look" different in that the sets contain different elements, they are indeed isomorphic: their structures are exactly the same. More generally, the direct product of two cyclic groups Z_n and Z_m is cyclic if and only if n and m are coprime.

Abstract examples

A relation-preserving isomorphism

If one object consists of a set X with a binary relation R and the other object consists of a set Y with a binary relation S then an isomorphism from X to Y is a bijective function f : X → Y such that

f(u) S f(v) if and only if u R v.

S is reflexive, irreflexive, symmetric, antisymmetric, asymmetric, transitive, total, trichotomous, a partial order, total order, strict weak order, total preorder (weak order), an equivalence relation, or a relation with any other special properties, if and only if R is.

For example, R is an ordering ≤ and S an ordering $\sqsubseteq$ , then an isomorphism from X to Y is a bijective function f : X → Y such that

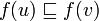$f(u) \sqsubseteq f(v)$ if and only if u ≤ v.

Such an isomorphism is called an order isomorphism or (less commonly) an isotone isomorphism.

If X = Y we have a relation-preserving automorphism.

An operation-preserving isomorphism

Suppose that on these sets X and Y, there are two binary operations 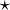$\star$ an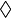d $\Diamond$ which happen to constitute the groups (X, 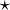$\star$ ) and (Y, 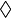$\Diamond$ ). Note that the operators operate on elements from the domain and range, respectively, of the "one-to-one" and "onto" function f. 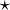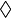There is an isomorphism from X to Y if the bijective function f : X → Y happens to produce results, that sets up a correspondence between the operator $\star$ and the operator $\Diamond$ .

$f(u) \Diamond f(v) = f(u \star v)$

for all u, v in X.

Applications

In abstract algebra, two basic isomorphisms are defined:

Group isomorphism, an isomorphism between groups
Ring isomorphism, an isomorphism between rings. (Note that isomorphisms between fields are actually ring isomorphisms)

Just as the automorphisms of an algebraic structure form a group, the isomorphisms between two algebras sharing a common structure form a heap. Letting a particular isomorphism identify the two structures turns this heap into a group.

In mathematical analysis, the Laplace transform is an isomorphism mapping hard differential equations into easier algebraic equations.

In category theory, Iet the category C consist of two classes, one of objects and the other of morphisms. Then a general definition of isomorphism that covers the previous and many other cases is: an isomorphism is a morphism f : a → b that has an inverse, i.e. there exists a morphism g : b → a with fg = 1_b and gf = 1_a. For example, a bijective linear map is an isomorphism between vector spaces, and a bijective continuous function whose inverse is also continuous is an isomorphism between topological spaces, called a homeomorphism.

In graph theory, an isomorphism between two graphs G and H is a bijective map f from the vertices of G to the vertices of H that preserves the "edge structure" in the sense that there is an edge from vertex u to vertex v in G if and only if there is an edge from f(u) to f(v) in H. See graph isomorphism.

In early theories of logical atomism, the formal relationship between facts and true propositions was theorized by Bertrand Russell and Ludwig Wittgenstein to be isomorphic.

In cybernetics, the Good Regulator or Conant-Ashby theorem is stated "Every Good Regulator of a system must be a model of that system". Whether regulated or self-regulating an isomorphism is required between regulator part and the processing part of the system.

External links

Isomorphism on PlanetMath
Eric W. Weisstein, Isomorphism at MathWorld.