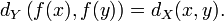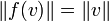Isometry
- For the mechanical engineering and architecture usage, see isometric projection. For isometry in differential geometry, see isometry (Riemannian geometry).
In mathematics, an isometry, isometric isomorphism or congruence mapping is a distance-preserving isomorphism between metric spaces. Geometric figures which can be related by an isometry are called congruent.
Isometries are often used in constructions where one space is embedded in another space. For instance, the completion of a metric space M involves an isometry from M into M', a quotient set of the space of Cauchy sequences on M. The original space M is thus isometrically isomorphic to a subspace of a complete metric space, and it is usually identified with this subspace. Other embedding constructions show that every metric space is isometrically isomorphic to a closed subset of some normed vector space and that every complete metric space is isometrically isomorphic to a closed subset of some Banach space.
Contents |
Definitions
The notion of isometry comes in two main flavors: global isometry and a weaker notion path isometry or arcwise isometry. Both are often called just isometry and one should determine from context which one is intended.
Let X and Y be metric spaces with metrics dY and dX. A map ƒ : X → Y is called distance preserving if for any x,y ∈ X one has
A distance preserving map is automatically injective. Clearly, every isometry between metric spaces is necessarily a topological imbedding.
A global isometry is a bijective distance preserving map. A path isometry or arcwise isometry is a map which preserves the lengths of curves (not necessarily bijective).
Two metric spaces X and Y are called isometric if there is an isometry from X to Y. The set of isometries from a metric space to itself forms a group with respect to function composition, called the isometry group.
Examples
- Any reflection, translation and rotation is a global isometry on Euclidean spaces. See also Euclidean group.
- The map R
 R defined by
R defined by 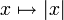 is a path isometry but not a global isometry.
is a path isometry but not a global isometry.
- The isometric linear maps from Cn to itself are the unitary matrices.
Linear isometries
Given two normed vector spaces V and W, a linear isometry is a linear map f : V → W that preserves the norms:
for all v in V. Linear isometries are distance-preserving maps in the above sense. They are global isometries if and only if they are surjective.
By the Mazur-Ulam theorem, any isometry of normed vector spaces over R is affine.
Generalizations
- Given a positive real number ε, an ε-isometry or almost isometry (also called a Hausdorff approximation) is a map
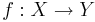 between metric spaces such that
between metric spaces such that
- for x,x′ ∈ X one has |dY(ƒ(x),ƒ(x′))−dX(x,x′)| < ε, and
- for any point y ∈ Y there exists a point x ∈ X with dY(y,ƒ(x)) < ε
- That is, an ε-isometry preserves distances to within ε and leaves no element of the codomain further than ε away from the image of an element of the domain. Note that ε-isometries are not assumed to be continuous.
- Quasi-isometry is yet another useful generalization.
Beckman-Quarles theorem
The Beckman-Quarles theorem states that for a Euclidean space E of dimension d at least 2, any mapping f from E to itself that preserves the property of being at a unit distance apart must be an isometry.
See also
- Congruence (geometry)
- Euclidean plane isometry
- 3D isometries which leave the origin fixed
- space group
- involution
- Isometries in physics
- Isometry group
- Homeomorphism group
References
- F. S. Beckman and D. A. Quarles, Jr., On isometries of Euclidean space, Proc. Amer. Math. Soc., 4 (1953) 810-815.