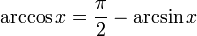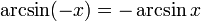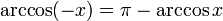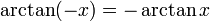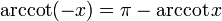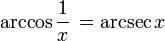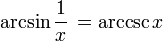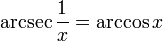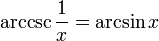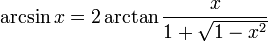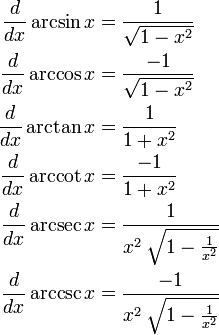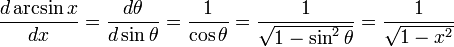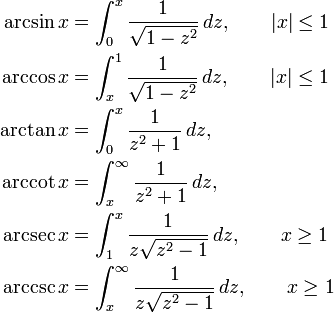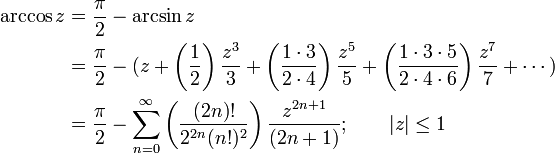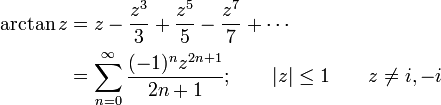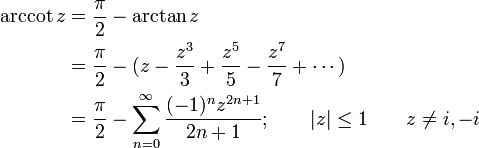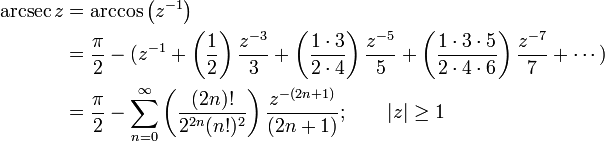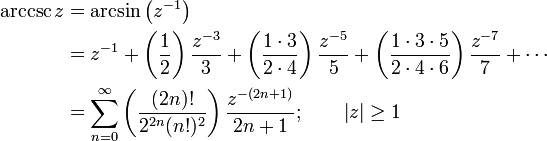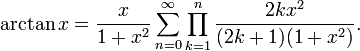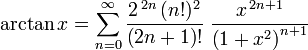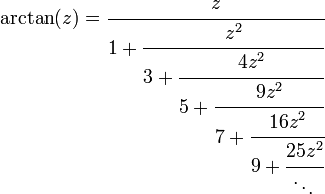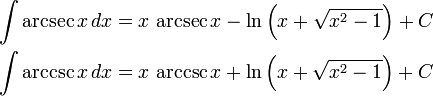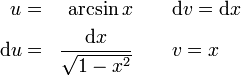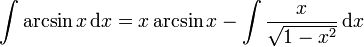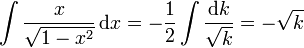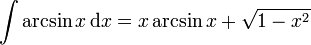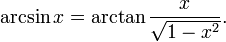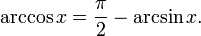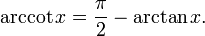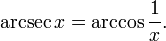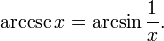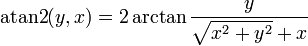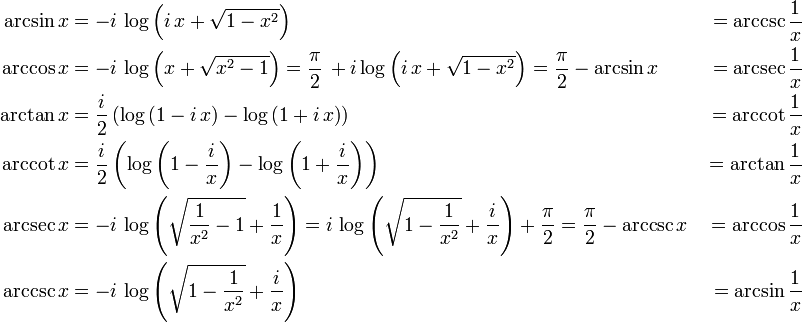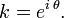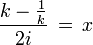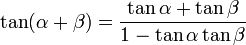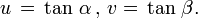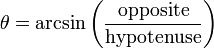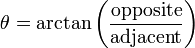Inverse trigonometric functions
In mathematics, the inverse trigonometric functions or cyclometric functions are the inverse functions of the trigonometric functions. The principal inverses are listed in the following table.
| Name | Usual notation | Definition | Domain of x for real result | Range of usual principal value |
|---|---|---|---|---|
| arcsine | y = arcsin(x) | x = sin(y) | −1 to +1 | −π/2 ≤ y ≤ π/2 |
| arccosine | y = arccos(x) | x = cos(y) | −1 to +1 | 0 ≤ y ≤ π |
| arctangent | y = arctan(x) | x = tan(y) | all | −π/2 < y < π/2 |
| arccotangent | y = arccot(x) | x = cot(y) | all | 0 < y < π |
| arcsecant | y = arcsec(x) | x = sec(y) | −∞ to −1 or 1 to ∞ | 0 ≤ y < π/2 or π/2 < y ≤ π |
| arccosecant | y = arccsc(x) | x = csc(y) | −∞ to −1 or 1 to ∞ | −π/2 ≤ y < 0 or 0 < y ≤ π/2 |
If x is allowed to be a complex number, then the range of y applies only to its real part.
The notations sin−1, cos−1, etc. are often used for arcsin, arccos, etc., but this convention logically conflicts with the common semantics for expressions like sin2(x), which do not refer to function composition but rather multiplication, and therefore may result in confusion between multiplicative inverse and compositional inverse.



| Trigonometry |
|
History |
| Reference |
|
List of identities |
| Euclidean theory |
|
Law of sines |
| Calculus |
|
The Trigonometric integral |
In computer programming languages the functions arcsin, arccos, arctan, are usually called asin, acos, atan. Many programming languages also provide the two-argument atan2 function, which computes the arctangent of y/x given y and x, but with a range of [−π, π].
Relationships among the inverse trigonometric functions
Complementary angles:
Negative arguments:
Reciprocal arguments:
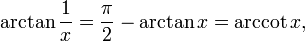 if
if 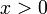
 if
if 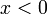
 if
if 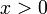
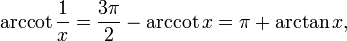 if
if 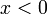
If you only have a fragment of a sine table:
 if
if 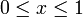
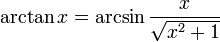
Notice that whenever the square root of a complex number is used here, we choose the root with the positive real part (or positive imaginary part if the square was negative real).
From the half-angle formula 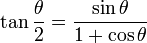 , we get:
, we get:
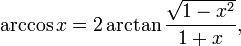 if
if 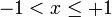
General solutions
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of 2π. Sine and cosecant begin their period at 2πk - π/2 (where k is an integer), finish it at 2πk + π/2, and then reverse themselves over 2πk + π/2 to 2πk + 3π/2. Cosine and secant begin their period at 2πk, finish it at 2πk + π, and then reverse themselves over 2πk + π to 2πk + 2π. Tangent begins its period at 2πk - π/2, finishes it at 2πk + π/2, and then repeats it (forward) over 2πk + π/2 to 2πk + 3π/2. Cotangent begins its period at 2πk, finishes it at 2πk + π, and then repeats it (forward) over 2πk + π to 2πk + 2π.
This periodicity is reflected in the general inverses:
- sin y = x if and only if y = arcsin x + 2kπ or y = π − arcsin x + 2kπ for some integer k.
- cos y = x if and only if y = arccos x + 2kπ or y = 2π − arccos x + 2kπ for some integer k.
- tan y = x if and only if y = arctan x + kπ for some integer k.
- cot y = x if and only if y = arccot x + kπ for some integer k.
- sec y = x if and only if y = arcsec x + 2kπ or y = 2π − arcsec x + 2kπ for some integer k.
- csc y = x if and only if y = arccsc x + 2kπ or y = π − arccsc x + 2kπ for some integer k.
Derivatives of inverse trigonometric functions
Simple derivatives for real and complex values of 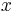 are as follows:
are as follows:
Only for real values of 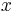 :
:
For a sample derivation: if  , we get:
, we get:
Expression as definite integrals
Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:
When x equals 1, the integrals with limited domains are improper integrals, but still well-defined.
Infinite series
Like the sine and cosine functions, the inverse trigonometric functions can be calculated using infinite series, as follows:
Leonhard Euler found a more efficient series for the arctangent, which is:
(Notice that the term in the sum for n= 0 is the empty product which is 1.)
Alternatively, this can be expressed:
Continued fraction for arctangent
An alternative to the power series for arctangent is its generalized continued fraction:
This is valid in the cut complex plane. There are two cuts, from −i to the point at infinity, going down the imaginary axis, and from i to the point at infinity, going up the same axis. It works best for real numbers running from −1 to 1. The partial denominators are the odd natural numbers, and the partial numerators (after the first) are just (nz)2, with each perfect square appearing once. It was developed by Carl Friedrich Gauss, utilizing the hypergeometric series.
Indefinite integrals of inverse trigonometric functions
For real and complex values of 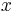 :
:
For real x≥1:
All of these can be derived using integration by parts and the simple derivative forms shown above.
Example proof
Using 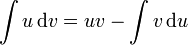 , set
, set
Then
Substitute 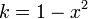 . Then
. Then 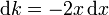 and
and
Back-substitute for x to yield
Recommended method of calculation
To calculate arcsine, use:
To calculate arccosine, use:
To calculate arctangent for x near zero, use the continued fraction above. To calculate arctangent for other values of x, use:
To calculate arccotangent, use:
To calculate arcsecant, use:
To calculate arccosecant, use:
Two argument variant of arctangent
The two-argument atan2 function computes the arctangent of y/x given y and x, but with a range of (−π, π]. In other words, atan2(y, x) is the angle between the positive x-axis of a plane and the point (x, y) on it, with positive sign for counter-clockwise angles (upper half-plane, y > 0), and negative sign for clockwise angles (lower half-plane, y < 0). It was first introduced in many computer programming languages, but it is now also common in other fields of science and engineering.
In terms of the standard arctan function, that is with range of (−π/2, π/2), it can be expressed as follows:
It also equals the principal value of the argument of the complex number x + iy.
This function may be computed using the tangent half-angle formulae as follows:
provided that either x > 0 or y ≠ 0. However this fails if given x ≤ 0 and y = 0.
The above argument order 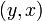 seems to be the most common, and in particular is used in ISO standards such as the C programming language, but a few authors may use the opposite convention
seems to be the most common, and in particular is used in ISO standards such as the C programming language, but a few authors may use the opposite convention  so some caution is warranted.
so some caution is warranted.
Logarithmic forms
These functions may also be expressed using complex logarithms. This extends in a natural fashion their domain to the complex plane.
Elementary proofs of these relations proceed via expansion to exponential forms of the trigonometric functions.
Example proof
 (exponential definition of sine)
(exponential definition of sine)
Let
Then
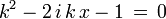 (solve for
(solve for 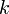 )
)
 (the positive branch is chosen)
(the positive branch is chosen)
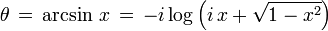 Q.E.D.
Q.E.D.
 |
 |
 |
 |
 |
 |
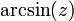 |
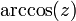 |
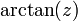 |
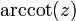 |
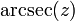 |
 |
Arctangent addition formula
Proof
start from
and let
Practical use
Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when you already know the length of the sides of the triangle. Remember the acronym SOHCAHTOA. Using inverse trigonometric functions
Often, the hypotenuse is unknown and would need to be calculated before using arcsin or arccos. Arctan comes in handy in this situation. You can compute the angle of the triangles without knowing the length of the hypotenuse.
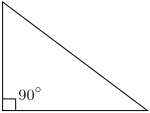
For example, you can calculate the slope of your roof line if you know the rise and run of the roof. If your roof drops 8 feet as it runs out 20 feet then your roof is angled θ degrees up from horizontal, where θ may be computed as follows.
See also
- Trigonometric function
- Tangent half-angle formula
- List of trigonometric identities
- Complex logarithm
- Square root
- Continued fraction of Gauss
External links
- Eric W. Weisstein, Inverse Trigonometric Functions at MathWorld.
- Eric W. Weisstein, Inverse Tangent at MathWorld.