Injective function

An injective function (injection)

Another injective function (this one is a bijection)

A non-injective function (this one happens to be a surjection)

In mathematics, an injective function is a function which associates distinct arguments with distinct values.

An injective function is called an injection, and is also said to be an information-preserving or one-to-one function (the latter is not to be confused with one-to-one correspondence, i.e. a bijective function).

A function f that is not injective is sometimes called many-to-one. (However, this terminology is also sometimes used to mean "single-valued", i.e. each argument is mapped to at most one value.)

A monomorphism is a generalization of an injective function in category theory.

Definition

Let f be a function whose domain is a set A. The function f is injective if, for all a and b in A, if f(a) = f(b) then a = b.

Examples

• For any set X, the identity function on X is injective.
• The function f : R → R defined by f(x) = 2x + 1 is injective.
• The function g : R → R defined by g(x) = x² is not injective, because (for example) g(1) = 1 = g(−1). However, if g is redefined so that its domain is the non-negative real numbers [0,+∞), then g is injective.
• The exponential function exp : R → R defined by exp(x) = e^x is injective (but not surjective as no value maps to a negative number).
• The natural logarithm function ln : (0, ∞) → R defined by x ↦ ln x is injective.
• The function g : R → R defined by g(x) = xⁿ − x is not injective, since, for example, g(0) = g(1).

More generally, when X and Y are both the real line R, then an injective function f : R → R is one whose graph is never intersected by any horizontal line more than once.

Injections can be undone

Functions with left inverses are always injections. That is, given f : X → Y, if there is a function g : Y → X such that, for every x ∈ X

g(f(x)) = x (f can be undone by g)

then f is injective. In this case, f is called a section of g and g is called a retraction of f.

Conversely, every injection f with non-empty domain has a left inverse g (in conventional mathematics^[1]). Note that g may not be a complete inverse of f because the composition in the other order, f ∘ g, may not be the identity on Y. In other words, a function that can be undone or "reversed", such as f, is not necessarily invertible (bijective). Injections are "reversible" but not always invertible.

Although it is impossible to reverse a non-injective (and therefore information-losing) function, you can at least obtain a "quasi-inverse" of it, that is a multiple-valued function.

Injections may be made invertible

In fact, to turn an injective function f : X → Y into a bijective (hence invertible) function, it suffices to replace its codomain Y by its actual range J = f(X). That is, let g : X → J such that g(x) = f(x) for all x in X; then g is bijective. Indeed, f can be factored as incl_J,Y ∘ g, where incl_J,Y is the inclusion function from J into Y.

Other properties

• If f and g are both injective, then f ∘ g is injective.

The composition of two injective functions is injective.

• If g ∘ f is injective, then f is injective (but g need not be).
• f : X → Y is injective if and only if, given any functions g, h : W → X, whenever f ∘ g = f ∘ h, then g = h. In other words, injective functions are precisely the monomorphisms in the category Set of sets.
• If f : X → Y is injective and A is a subset of X, then f ⁻¹(f(A)) = A. Thus, A can be recovered from its image f(A).
• If f : X → Y is injective and A and B are both subsets of X, then f(A ∩ B) = f(A) ∩ f(B).
• Every function h : W → Y can be decomposed as h = f ∘ g for a suitable injection f and surjection g. This decomposition is unique up to isomorphism, and f may be thought of as the inclusion function of the range h(W) of h as a subset of the codomain Y of h.
• If f : X → Y is an injective function, then Y has at least as many elements as X, in the sense of cardinal numbers. In particular, if, in addition, there is an injection from 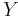to 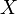, then 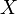and 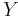has the same cardinal number. (This is known as the Cantor–Bernstein–Schroeder theorem.)
• If both X and Y are finite with the same number of elements, then f : X → Y is injective if and only if f is surjective.
• Every embedding is injective.

See also

• surjective function
• Injective module
• Horizontal line test
• Injective metric space

Notes

1. ↑ This principle is valid in conventional mathematics, but may fail in constructive mathematics. For instance, a left inverse of the inclusion {0,1} → R of the two-element set in the reals violates indecomposability by giving a retraction of the real line to the set {0,1}.

References

• Bartle, Robert G. (1976), The Elements of Real Analysis (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-05464-1 , p. 17 ff.
• Halmos, Paul R. (1974), Naive Set Theory, ISBN 978-0-387-90092-6 , p. 38 ff.