Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures.
The study of morphisms and of the structures (called objects) over which they are defined, is central to category theory. Much of the terminology of morphisms, as well as the intuition underlying them, comes from concrete categories, where the objects are simply sets with some additional structure, and morphisms are functions preserving this structure. Nevertheless, morphisms are not necessarily functions, and objects over which morphisms are defined are not necessarily sets. Instead, a morphism is often thought of as an arrow linking an object called the domain to another object called the codomain. Hence morphisms do not so much map sets into sets, as embody a relationship between some posited domain and codomain.
The notion of morphism recurs in much of contemporary mathematics. In set theory, morphisms are functions; in topology, continuous functions; in universal algebra, homomorphisms; in group theory, group homomorphisms.
Contents |
Definition
A category C consists of two classes, one of objects and the other of morphisms.
There are two operations defined on every morphism, the domain (or source) and the codomain (or target).
If a morphism f has domain X and codomain Y, we write f : X → Y. Thus a morphism is an arrow from its domain to its codomain. The set of all morphisms from X to Y is denoted homC(X,Y) or simply hom(X, Y) and called the hom-set between X and Y. (Some authors write MorC(X,Y) or Mor(X, Y)).
For every three objects X, Y, and Z, there exists a binary operation hom(X, Y) × hom(Y, Z) → hom(X, Z) called composition. The composite of f : X → Y and g : Y → Z is written g o f or gf. The composition of morphisms is often represented by a commutative diagram. For example,
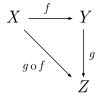
Morphisms satisfy two axioms:
- Identity: for every object X, there exists a morphism idX : X → X called the identity morphism on X, such that for every morphism f : A → B we have idB o f = f = f o idA.
- Associativity: h o (g o f) = (h o g) o f whenever the operations are defined.
When C is a concrete category, the identity morphism is just the identity function, and composition is just the ordinary composition of functions. Associativity then follows, because the composition of functions is associative.
Note that the domain and codomain are in fact part of the information determining a morphism. For example, in the category of sets, where morphisms are functions, two functions may be identical as sets of ordered pairs (may have the same range), while having different codomains. The two functions are distinct from the viewpoint of category theory. Thus many authors require that the hom-classes hom(X, Y) be disjoint. In practice, this is not a problem because if this disjointness does not hold, it can be assured by appending the domain and codomain to the morphisms, (say, as the second and third components of an ordered triple).
Alternate definition using a "null morphism"
Since there is exactly one identity morphism idX for each object X, the class of objects can be dropped from the definition of a category, and replaced with the subclass of homC consisting of the identity morphisms. In this formulation, a category C consists of a non-empty class homC with one additional structure: the composition function, a binary operation o: homC × homC → homC. Composition is defined for all pairs of morphisms (elements of homC), with the help of a null morphism (or just null) ø in homC, which obeys fø = øf = ø for every morphism f. The class C0 of identity morphisms (or just identities) consists of those elements X≠ø of homC such that, for every g in homC, 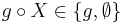 . Up to isomorphism, the only category with no identities is the null category 0 = {ø} (equipped with the obvious composition function).
. Up to isomorphism, the only category with no identities is the null category 0 = {ø} (equipped with the obvious composition function).
In order to form a category, the composition operation must be associative and must also split over the identity morphisms, meaning that:
- For every f≠ø in homC, fX must be non-null (and equal to f) for exactly one X in C0 (the domain of f).
- For every g≠ø in homC, Yg must be non-null (and equal to g) for exactly one Y in C0 (the codomain of g).
- Consequently, domain(f) = codomain(g) is a necessary condition for fg to be non-null. This must also be a sufficient condition.
Thus the class homC of morphisms is the union of the non-overlapping classes 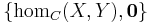 . The domain homC × homC of the composition operation may be divided into the null sector
. The domain homC × homC of the composition operation may be divided into the null sector 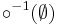 and the collection of non-null sectors homC(X,Y) × homC(Y,Z).
and the collection of non-null sectors homC(X,Y) × homC(Y,Z).
The two definitions of a category are equivalent, but the formulation with the "null morphism" has several advantages:
- We can identify the category with its class of morphisms (including the null morphism), and write C for both. Thus a category is simply a non-empty class C, equipped with an associative binary operation with null ø, which splits over a subclass C0 of identities.
- The composition operation is a total function on C × C; instead of splitting C into hom-classes and enumerating cases in which composition is and isn't defined, one can usually make simpler statements about the preimage of ø.
- Statements about the objects of the category reduce to statements about the subclass C0 of identity morphisms in homC, and can often be subsumed into facts about identity morphisms. For instance, a (total) functor F from category C to category D is just a function which preserves the composition operation (including its null and its subclass of identities). The statement that F preserves the identity subclass implies that
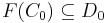 ; the mapping of objects given in the usual definition of a functor is recovered as the restriction of F to C0.
; the mapping of objects given in the usual definition of a functor is recovered as the restriction of F to C0. - We obtain a null category 0 = {ø}, distinct from the trivial category 1 = {1, ø}. (The trivial category is equipped with the only composition operation under which 1 is not equivalent to ø.) This null category serves as a zero object in the category of small categories Cat, if we take the morphisms of Cat to include all partial functors: maps F: C → D which preserve the composition operation (and its null) and map C0 into
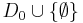 . (Note that "partial functor" is usually used in a different sense, analogous to the use of partial function to describe a function of several variables in which some have already been fixed.)
. (Note that "partial functor" is usually used in a different sense, analogous to the use of partial function to describe a function of several variables in which some have already been fixed.)
This version of the category of small categories is not the same as the usual definition of Cat, in which the class of morphisms is limited to the total functors, and thus the empty category ∅ = {} is an initial object but the terminal object is 1 = {1}. Statements about functors can be clearly divided into those which apply also to partial functors and those which apply only to total functors (those with kernel 0). Similarly, one can define a version of the category of sets in which the morphisms are the partial functions and the null set is a zero object; the total functions are those partial functions whose kernel is the null set. These examples illustrate that the essential property of a category is not its class of objects, nor even its class of morphisms, but its composition operation. This operation is usually implicit in the name of the class of morphisms; thus it would perhaps be better to name a category after its morphisms (e. g., the "category of total functions" vs. the "category of partial functions") rather than after its objects (the "category of sets").
Some specific morphisms
- Monomorphism: f : X → Y is called a monomorphism if f o g1 = f o g2 implies g1 = g2 for all morphisms g1, g2 : Z → X.
It is also called a mono or a monic. The morphism f has a left inverse if there is a morphism g:Y → X such that g o f = idX. The left inverse g is also called a retraction of f. Morphisms with left inverses are always monomorphisms, but the converse is not always true in every category; a monomorphism may fail to have a left-inverse.
A split monomorphism h : X → Y is a monomorphism having a left inverse g : Y → X, so that g o h = idX. Thus h o g : Y → Y is idempotent, so that (h o g)2 = h o g.
In concrete categories, a function which has left inverse is injective. Thus in concrete categories, monomorphisms are often, but not always, injective. The condition of being an injection is stronger than that of being a monomorphism, but weaker than that of being a split monomorphism.
- Epimorphism: Dually, f : X → Y is called an epimorphism if g1 o f = g2 o f implies g1 = g2 for all morphisms g1, g2 : Y → Z. It is also called an epi or an epic. The morphism f has a right-inverse if there is a morphism g : Y → X such that f o g = idY. The right inverse g is also called a section of f. Morphisms having a right inverse are always epimorphisms, but the converse is not always true in every category, as an epimorphism may fail to have a right inverse.
A split epimorphism is an epimorphism having a right inverse.
In concrete categories, a function which has a right inverse is surjective. Thus in concrete categories, epimorphisms are often, but not always, surjective. The condition of being a surjection is stronger than that of being an epimorphism, but weaker than that of being a split epimorphism. In the category of sets, every surjection has a section, a result equivalent to the axiom of choice.
Note that if a split monomorphism f has a left-inverse g, then g is a split epimorphism and has right-inverse f.
- A bimorphism is a morphism that is both an epimorphism and a monomorphism.
- Isomorphism: f : X → Y is called an isomorphism if there exists a morphism g : Y → X such that f o g = idY and g o f = idX.
If a morphism has both left-inverse and right-inverse, then the two inverses are equal, so f is an isomorphism, and g is called simply the inverse of f. Inverse morphisms, if they exist, are unique. The inverse g is also an isomorphism with inverse f. Two objects with an isomorphism between them are said to be isomorphic or equivalent.
Note that while every isomorphism is a bimorphism, a bimorphism is not necessarily an isomorphism. For example, in the category of commutative rings the inclusion Z → Q is a bimorphism which is not an isomorphism. However, any morphism that is both an epimorphism and a split monomorphism, or both a monomorphism and a split epimorphism, must be an isomorphism. A category, such as Set, in which every bimorphism is an isomorphism is known as a balanced category.
- Endomorphism: f : X → X is an endomorphism of X.
A split endomorphism is an idempotent endomorphism f if f admits a decomposition f = h o g with g o h = id. In particular, the Karoubi envelope of a category splits every idempotent morphism.
- An automorphism is a morphism that is both an endomorphism and an isomorphism.
Examples
- In the concrete categories studied in universal algebra (groups, rings, modules, etc.), morphisms are called homomorphisms. Likewise, the notions of automorphism, endomorphism, epimorphism, homeomorphism, isomorphism, and monomorphism all find use in universal algebra.
- In the category of topological spaces, morphisms are continuous functions and isomorphisms are called homeomorphisms.
- In the category of smooth manifolds, morphisms are smooth functions and isomorphisms are called diffeomorphisms.
- In the category of small categories, functors can be thought of as morphisms.
- In a functor category, the morphisms are natural transformations.
For more examples, see the entry category theory.
See also
- anamorphism
- automorphism
- catamorphism
- category theory
- concrete category
- diffeomorphism
- endomorphism
- epimorphism
- holomorphic function
- homeomorphism
- homomorphism
- hylomorphism
- isomorphism
- monomorphism
- normal morphism
- paramorphism
- zero morphism
External links
- Category on PlanetMath
- TypesOfMorphisms on PlanetMath