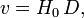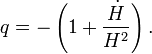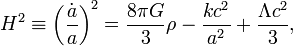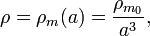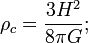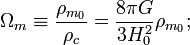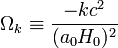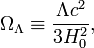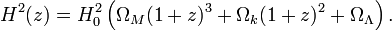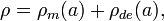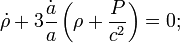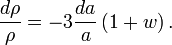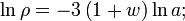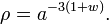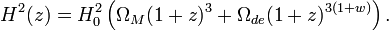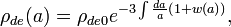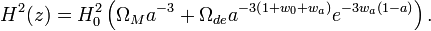Hubble's law
| Physical cosmology | ||||||||||||||
 |
||||||||||||||
| Universe · Big Bang Age of the Universe Timeline of the Big Bang Ultimate fate of the universe
|
||||||||||||||
Hubble's law is the statement in physical cosmology that the redshift in light coming from distant galaxies is proportional to their distance. The law was first formulated by Edwin Hubble in 1929[1] after nearly a decade of observations. It is considered the first observational basis for the expanding space paradigm and today serves as one of the pieces of evidence most often cited in support of the Big Bang. The most recent calculation of the proportionality constant used 2003 data from the satellite WMAP combined with other astronomical data, and yielded a value of H0 = 70.1 ± 1.3 (km/s)/Mpc. This value agrees well with that of H0 = 72 ± 8 km/s/Mpc obtained in 2001 by using NASA's Hubble Space Telescope[2]. In August, 2006, a less precise figure was obtained independently using data from NASA's orbital Chandra X-ray Observatory: H0 = 77 (km/s)/Mpc or about 2.5×10−18 s−1 with an uncertainty of ± 15%.[3] NASA summarizes existing data to indicate a constant of 70.8 ± 1.6 (km/s)/Mpc if spacetime is assumed to be flat, or 70.8 ± 4.0 (km/s)/Mpc otherwise.[4] [2.3×10−18 s−1 = 1/(13.8 billion years)]
Contents |
Discovery
A decade before Hubble made his observations, a number of physicists and mathematicians had established a consistent theory of the relationship between space and time by using Einstein's field equations of general relativity. Applying the most general principles to the nature of the universe yielded a dynamic solution that conflicted with the then prevailing notion of a static universe.
FLRW equations
In 1922, Alexander Friedmann derived his Friedmann equations from Einstein's field equations, showing that the universe might expand at a rate calculable by the equations.[5] The parameter used by Friedmann is known today as the scale factor which can be considered as a scale invariant form of the proportionality constant of Hubble's Law. Georges Lemaître independently found a similar solution in 1927. The Friedmann equations are derived by inserting the metric for a homogeneous and isotropic universe into Einstein's field equations for a fluid with a given density and pressure. This idea of an expanding spacetime would eventually lead to the Big Bang and Steady State theories of cosmology.
Shape of the universe
Before the advent of modern cosmology, there was considerable talk about the size and shape of the universe. In 1920, the famous Shapley-Curtis debate took place between Harlow Shapley and Heber D. Curtis over this issue. Shapley argued for a small universe the size of the Milky Way galaxy and Curtis argued that the universe was much larger. The issue was resolved in the coming decade with Hubble's improved observations.
Cepheid variable stars outside of the Milky Way
Edwin Hubble did most of his professional astronomical observing work at Mount Wilson Observatory, the world's most powerful telescope at the time. His observations of Cepheid variable stars in spiral nebulae enabled him to calculate the distances to these objects. Surprisingly, these objects were discovered to be at distances which placed them well outside the Milky Way. They continued to be called "nebulae" and it was only gradually that the term "galaxies" took over.
Combining redshifts with distance measurements
Combining his measurements of galaxy distances with Vesto Slipher's measurements of the redshifts associated with the galaxies, Hubble discovered a rough proportionality of the objects' distances. Though there was considerable scatter (now known to be caused by peculiar velocities), Hubble was able to plot a trend line from the 46 galaxies he studied and obtain a value for the Hubble constant of 500 km/s/Mpc (much higher than the currently accepted value due to errors in his distance calibrations). (See cosmic distance ladder for details.)
In 1958, the first good estimate of H0, 75 km/s/Mpc, was published by Allan Sandage,[6] but it would be decades before a consensus was achieved.
The cosmological constant abandoned
After Hubble's discovery was published, Albert Einstein abandoned his work on the cosmological constant (which he had designed to allow for a static solution to his equations). He later termed this work his "greatest blunder" since the assumption of a static universe had prevented him from predicting the expanding universe. Einstein made a famous trip to Mount Wilson in 1931 to thank Hubble for providing the observational basis for modern cosmology.
Interpretation
The discovery of the linear relationship between redshift, interpreted as recessional velocity, and distance yields a straightforward mathematical expression for Hubble's Law as follows:
where
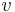 is the recessional velocity, typically expressed in km/s.
is the recessional velocity, typically expressed in km/s.- H0 is Hubble's constant and corresponds to the value of
 (often termed the Hubble parameter which is a value that is time dependent) in the Friedmann equations taken at the time of observation denoted by the subscript 0. This value is the same throughout the universe for a given comoving time.
(often termed the Hubble parameter which is a value that is time dependent) in the Friedmann equations taken at the time of observation denoted by the subscript 0. This value is the same throughout the universe for a given comoving time. 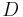 is the comoving proper distance from the galaxy to the observer, measured in megaparsecs (Mpc), in the 3-space defined by given cosmological time. (Recession velocity is just v = dD/dt).
is the comoving proper distance from the galaxy to the observer, measured in megaparsecs (Mpc), in the 3-space defined by given cosmological time. (Recession velocity is just v = dD/dt).
Observability of parameters
Strictly speaking, neither v nor D in the formula are directly observable, because they are properties now of a galaxy, whereas our observations refer to the galaxy in the past, at the time that the light we currently see left it.
For relatively nearby galaxies (redshift z much less than unity), v and D will not have changed much, and v can be estimated using the formula 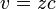 where c is the speed of light. This gives the empirical relation found by Hubble.
where c is the speed of light. This gives the empirical relation found by Hubble.
For distant galaxies, v (or D) cannot be calculated from z without specifying a detailed model for how H changes with time. The redshift is not even directly related to the recession velocity at the time the light set out, but it does have a simple interpretation: (1+z) is the factor by which the universe has expanded while the photon was travelling towards the observer.
Expansion velocity vs relative velocity
In using Hubble's law to determine distances, only the velocity due to the expansion of the universe can be used. Since gravitationally interacting galaxies move relative to each other independent of the expansion of the universe, these relative velocities, called peculiar velocities, need to be accounted for in the application of Hubble's law.
The Finger of God effect is one result of this phenomenon discovered in 1938 by Benjamin Kenneally. In systems that are gravitationally bound, such as galaxies or our planetary system, the expansion of space is (more than) annihilated by the attractive force of gravity.
Idealized Hubble's Law
The mathematical derivation of an idealized Hubble's Law for a uniformly expanding universe is a fairly elementary theorem of geometry in 3-dimensional Cartesian/Newtonian coordinate space, which, considered as a metric space, is entirely homogeneous and isotropic (properties do not vary with location or direction). Simply stated the theorem is this:
- Any two points which are moving away from the origin, each along straight lines and with speed proportional to distance from the origin, will be moving away from each other with a speed proportional to their distance apart.
In fact this applies to non-Cartesian spaces as long as they are locally homogeneous and isotropic; specifically to the negatively- and positively-curved spaces frequently considered as cosmological models (see shape of the universe).
The Ultimate fate and age of the universe

The value of the Hubble parameter changes over time either increasing or decreasing depending on the sign of the so-called deceleration parameter 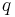 which is defined by
which is defined by
In a universe with a deceleration parameter equal to zero, it follows that H = 1/t, where t is the time since the Big Bang. A non-zero, time-dependent value of 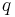 simply requires integration of the Friedmann equations backwards from the present time to the time when the comoving horizon size was zero.
simply requires integration of the Friedmann equations backwards from the present time to the time when the comoving horizon size was zero.
It was long thought that q was positive, indicating that the expansion is slowing down due to gravitational attraction. This would imply an age of the universe less than 1/H (which is about 14 billion years). For instance, a value for q of 1/2 (once favoured by most theorists) would give the age of the universe as 2/(3H). The discovery in 1998 that q is apparently negative means that the universe could actually be older than 1/H. In fact, estimates of the age of the universe are, by coincidence, very close to 1/H.
Olbers' paradox
The expansion of space summarized by the Big Bang interpretation of Hubble's Law is relevant to the old conundrum known as Olbers' paradox: if the universe were infinite, static, and filled with a uniform distribution of stars (notice that this also requires an infinite number of stars), then every line of sight in the sky would end on a star, and the sky would be as bright as the surface of a star. However, the night sky is largely dark. Since the 1600s, astronomers and other thinkers have proposed many possible ways to resolve this paradox, but the currently accepted resolution depends in part upon the Big Bang theory and in part upon the Hubble expansion. In a universe that exists for a finite amount of time, only the light of finitely many stars has had a chance to reach us yet, and the paradox is resolved. Additionally, in an expanding universe distant objects recede from us, which causes the light emanating from them to be redshifted and diminished in brightness. Although both effects contribute, the redshift is the less important of the two; remember the original paradox was couched in terms of a static universe.[7]
Determining the Hubble constant
The value of the Hubble constant is estimated by measuring the redshift of distant galaxies and then determining the distances to the same galaxies (by some other method than Hubble's law). Uncertainties in the physical assumptions used to determine these distances have caused varying estimates of the Hubble constant. For most of the second half of the 20th century the value of 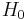 was estimated to be between 50 and 90 (km/s)/Mpc.
was estimated to be between 50 and 90 (km/s)/Mpc.
Disputes over Hubble's constant
The value of the Hubble constant was the topic of a long and rather bitter controversy between Gérard de Vaucouleurs who claimed the value was around 100 and Allan Sandage who claimed the value was near 50.
In 1996, a debate moderated by John Bahcall between Gustav Tammann and Sidney van den Bergh was held in similar fashion to the earlier Shapley-Curtis debate over these two competing values.
This difference was partially resolved with the introduction of the ΛCDM model of the universe in the late 1990s.
The ΛCDM model
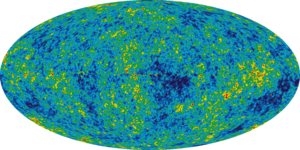
With the ΛCDM model observations of high-redshift clusters at X-ray and microwave wavelengths using the Sunyaev-Zel'dovich effect, measurements of anisotropies in the cosmic microwave background radiation, and optical surveys all gave a value of around 70 for the constant.
Using Hubble space telescope data
In particular the Hubble Key Project (led by Dr. Wendy L. Freedman, Carnegie Observatories) gave the most accurate optical determination in May 2001 with its final estimate[8] of 72±8 (km/s)/Mpc, consistent with a measurement of 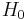 based upon Sunyaev-Zel'dovich effect observations of many galaxy clusters having a similar accuracy.
based upon Sunyaev-Zel'dovich effect observations of many galaxy clusters having a similar accuracy.
Using WMAP data
The most precise cosmic microwave background radiation determinations were 71±4 (km/s)/Mpc, by WMAP in 2003, and 70.4+1.5−1.6 (km/s)/Mpc, for measurements up to 2006.[9] The five year release from WMAP in 2008 finds 71.9+2.6−2.7 (km/s)/Mpc.[1]
These values arise from fitting a combination of WMAP and other cosmological data to the simplest version of the ΛCDM model. If the data is fitted with more general versions, 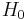 tends to be smaller and more uncertain: typically around 67±4 (km/s)/Mpc although some models allow values near 63 (km/s)/Mpc.[10]
tends to be smaller and more uncertain: typically around 67±4 (km/s)/Mpc although some models allow values near 63 (km/s)/Mpc.[10]
Using Chandra X-ray Observatory data
In August 2006, using NASA's Chandra X-ray Observatory, a team from NASA's Marshall Space Flight Center (MSFC) found the Hubble constant to be 77 (km/s)/Mpc, with an uncertainty of about 15%.[11] The consistency of the measurements from all these methods lends support to both the measured value of 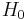 and the ΛCDM model.
and the ΛCDM model.
Acceleration of the expansion
A value for 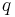 measured from standard candle observations of Type Ia supernovae, which was determined in 1998 to be negative, surprised many astronomers with the implication that the expansion of the universe is currently "accelerating" (although the Hubble factor is still decreasing with time; see the articles on dark energy and the ΛCDM model).
measured from standard candle observations of Type Ia supernovae, which was determined in 1998 to be negative, surprised many astronomers with the implication that the expansion of the universe is currently "accelerating" (although the Hubble factor is still decreasing with time; see the articles on dark energy and the ΛCDM model).
Derivation of the Hubble parameter
Start with the Friedman equation:
where  is the Hubble parameter,
is the Hubble parameter,  is the scale factor, G is the gravitational constant,
is the scale factor, G is the gravitational constant, 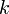 is the normalised spatial curvature of the universe and equal to −1, 0, or +1, and
is the normalised spatial curvature of the universe and equal to −1, 0, or +1, and  is the cosmological constant.
is the cosmological constant.
Matter-dominated universe (with a cosmological constant)
If the universe is matter-dominated, then the mass density of the universe 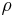 can just be taken to include matter so
can just be taken to include matter so
where 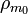 is the density of matter today. We know for nonrelativistic particles that their mass density decreases proportional to the inverse volume of the universe so the equation above must be true. We can also define (see density parameter for
is the density of matter today. We know for nonrelativistic particles that their mass density decreases proportional to the inverse volume of the universe so the equation above must be true. We can also define (see density parameter for 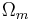 )
)
so 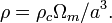 Also, by definition,
Also, by definition,
and
where the subscript nought refers to the values today, and 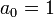 . Substituting all of this in into the Friedman equation at the start of this section and replacing
. Substituting all of this in into the Friedman equation at the start of this section and replacing  with
with 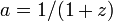 gives
gives
Matter- and dark energy-dominated universe
If the universe is both matter-dominated and dark energy-dominated, then the above equation for the Hubble parameter will also be a function of the equation of state of dark energy. So now:
where 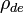 is the mass density of the dark energy. By definition an equation of state in cosmology is
is the mass density of the dark energy. By definition an equation of state in cosmology is 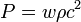 , and if we substitute this into the fluid equation, which describes how the mass density of the universe evolves with time,
, and if we substitute this into the fluid equation, which describes how the mass density of the universe evolves with time,
If w is constant,
Therefore for dark energy with a constant equation of state w, 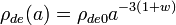 . If we substitute this into the Friedman equation in a similar way as before, but this time set
. If we substitute this into the Friedman equation in a similar way as before, but this time set 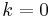 which is assuming we live in a spatially flat universe, (see Shape of the Universe)
which is assuming we live in a spatially flat universe, (see Shape of the Universe)
If dark energy does not have a constant equation-of-state w, then
and to solve this we must parametrize 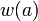 , for example if
, for example if 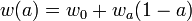 , giving
, giving
Units derived from the Hubble constant
Hubble time
The Hubble constant 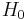 has units of inverse time. We can therefore define “Hubble time” as
has units of inverse time. We can therefore define “Hubble time” as 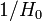 . The value of Hubble time in the standard cosmological model is 4.35×1017 s or 13.8 billion years (Liddle 2003, p. 57). The phrase "expansion timescale" means "Hubble time".[2]
. The value of Hubble time in the standard cosmological model is 4.35×1017 s or 13.8 billion years (Liddle 2003, p. 57). The phrase "expansion timescale" means "Hubble time".[2]
Hubble length
The Hubble length is a unit of distance in cosmology, defined as 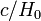 —the speed of light multiplied by the Hubble time. It is equivalent to 4228 million parsecs or 13.8 billion light years. (The numerical value of the Hubble length in light years is, by definition, equal to that of the Hubble time in years.)
—the speed of light multiplied by the Hubble time. It is equivalent to 4228 million parsecs or 13.8 billion light years. (The numerical value of the Hubble length in light years is, by definition, equal to that of the Hubble time in years.)
Hubble volume
The Hubble volume is sometimes defined as a volume of the universe with a comoving size of 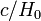 . The exact definition varies: it is sometimes defined as the volume of a sphere with radius
. The exact definition varies: it is sometimes defined as the volume of a sphere with radius 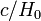 , or alternatively, a cube of side
, or alternatively, a cube of side 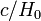 . Some cosmologists even use the term Hubble volume to refer to the volume of the observable universe, although this has a radius approximately 3 times larger.
. Some cosmologists even use the term Hubble volume to refer to the volume of the observable universe, although this has a radius approximately 3 times larger.
See also
- Age of the universe
- Shape of the universe
- Hyperbolic geometry (crinkly due to expansion)
- Euclidean geometry (flat due to a balance)
- Elliptic geometry (round due to gravity)
Notes
- ↑ Hubble, Edwin, "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae" (1929) Proceedings of the National Academy of Sciences of the United States of America, Volume 15, Issue 3, pp. 168-173 (Full article, PDF)
- ↑ W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, R. C. Kennicutt, Jr., H. C. Ford, J. A. Graham, J. P. Huchra, S. M. G. Hughes, G. D. Illingworth, L. M. Macri, P. B. Stetson (2001). "Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant". The Astrophysical Journal 553 (1): 47–72. doi:. http://adsabs.harvard.edu/cgi-bin/nph-bib_query?2001ApJ...553...47F.
- ↑ "Chandra Confirms the Hubble Constant" (2006-08-08). Retrieved on 2007-03-07.
- ↑ "WMAP's Universe". NASA.
- ↑ Friedman, A: Über die Krümmung des Raumes, Z. Phys. 10 (1922), 377-386. (English translation in: Gen. Rel. Grav. 31 (1999), 1991-2000.)
- ↑ Huchra, John. "The Hubble Constant". Retrieved on 2007-10-04.
- ↑ S. I. Chase, Olbers' Paradox, entry in the Physics FAQ; see also I. Asimov, "The Black of Night", in Asimov on Astronomy (Doubleday, 1974), ISBN 0-385-04111-X.
- ↑ W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, R. C. Kennicutt, Jr., H. C. Ford, J. A. Graham, J. P. Huchra, S. M. G. Hughes, G. D. Illingworth, L. M. Macri, P. B. Stetson (2001). "Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant". The Astrophysical Journal 553 (1): 47–72. doi:. http://adsabs.harvard.edu/cgi-bin/nph-bib_query?2001ApJ...553...47F.. Preprint available here.
- ↑ D. N. Spergel et al. (2007), "Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology", Astrophysical Journal Supplement Series 170: 377–408, doi:; available online at LAMBDA
- ↑ Results for
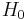 and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website.
and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website. - ↑ Chandra independently determines Hubble constant in Spaceflight Now
References
- Kutner, Marc (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 0-521-52927-1.
- Hubble, E.P.., The Observational Approach to Cosmology (Oxford, 1937)
- Liddle, A (2003). "An Introduction to Modern Cosmology 2nd ed.", Wiley.