Homotopy

In topology, two continuous functions from one topological space to another are called homotopic (Greek homos = identical and topos = place) if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions. An outstanding use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology.
In practice, there are technical difficulties in using homotopies with certain pathological spaces. Consequently most algebraic topologists work with compactly generated spaces, CW complexes, or spectra.
Contents |
Formal definition

Formally, a homotopy between two continuous functions f and g from a topological space X to a topological space Y is defined to be a continuous function H: X × [0,1] → Y from the product of the space X with the unit interval [0,1] to Y such that, for all points x in X, H(x,0)=f(x) and H(x,1)=g(x).
If we think of the second parameter of H as "time", then H describes a "continuous deformation" of f into g: at time 0 we have the function f, at time 1 we have the function g.
An alternative notation is to say that a homotopy between two continuous functions f , g : X → Y is a family of continuous functions ht: X → Y for t ∈ [0,1] such that h0= f and h1= g and the map t → ht is continuous from [0,1] to the space of all continuous functions X → Y. The two versions coincide by setting ht(x) = H(x,t).
Properties
Continuous functions f and g (both from topological space X to Y) are said to be homotopic if and only if there is a homotopy H taking f to g as described above. Being homotopic is an equivalence relation on the set of all continuous functions from X to Y. This homotopy relation is compatible with function composition in the following sense: if f1, g1: X → Y are homotopic, and f2, g2: Y → Z are homotopic, then their compositions f2 o f1 and g2 o g1: X → Z are homotopic as well.
Homotopy equivalence and null-homotopy
Given two spaces X and Y, we say they are homotopy equivalent or of the same homotopy type if there exist continuous maps f: X → Y and g: Y → X such that g o f is homotopic to the identity map idX and f o g is homotopic to idY.
The maps f and g are called homotopy equivalences in this case. Clearly, every homeomorphism is a homotopy equivalence, but the converse is not true: for example, a solid disk is not homeomorphic to a single point, although the disk and the point are homotopy equivalent.
Intuitively, two spaces X and Y are homotopy equivalent if they can be transformed into one another by bending, shrinking and expanding operations. For example, a solid disk or solid ball is homotopy equivalent to a point, and R2 − {(0,0)} is homotopy equivalent to the unit circle S1. Spaces that are homotopy equivalent to a point are called contractible.
A function f is said to be null-homotopic if it is homotopic to a constant function. (The homotopy from f to a constant function is then sometimes called a null-homotopy.) For example, a map from the circle S1 is null-homotopic precisely when it can be extended to a map of the disc D2.
It follows from these definitions that a space X is contractible if and only if the identity map from X to itself—which is always a homotopy equivalence—is null-homotopic.
Homotopy invariance
Homotopy equivalence is important because in algebraic topology many concepts are homotopy invariant, that is, they respect the relation of homotopy equivalence. For example, if X and Y are homotopy equivalent spaces, then:
- if X is path-connected, then so is Y
- if X is simply connected, then so is Y
- the (singular) homology and cohomology groups of X and Y are isomorphic
- if X and Y are path-connected, then the fundamental groups of X and Y are isomorphic, and so are the higher homotopy groups. Without the path-connectedness assumption, one has π1(X, x0) isomorphic to π1(Y, f(x0)) where f: X → Y is a homotopy equivalence and x0 a given point in X.
An example of an algebraic invariant of topological spaces which is not homotopy-invariant is compactly supported homology (which is, roughly speaking, the homology of the compactification, and compactification is not homotopy-invariant).
Relative homotopy
In order to define the fundamental group, one needs the notion of homotopy relative to a subspace. These are homotopies which keep the elements of the subspace fixed. Formally: if f and g are continuous maps from X to Y and K is a subset of X, then we say that f and g are homotopic relative to K if there exists a homotopy H: X × [0,1] → Y between f and g such that H(k,t) = f(k) = g(k) for all k∈K and t∈[0,1]. Also, if g is a retract from X to K and f is the identity map, this is known as a strong deformation retract of X to K.
Homotopy groups
Since the relation of two functions f , g : X → Y being homotopic relative to a subspace is an equivalence relation, we can look at the equivalence classes of maps between a fixed X and Y. If we fix X = [0,1]n, the unit interval [0,1] crossed with itself n times, and we take our subspace to be the its boundary ∂([0,1]n ) then the equivalence classes form a group, denoted πn(Y , y0 ), where y0 is the image of the subspace ∂([0,1]n ).
We can define the action of one equivalence class on another, and so we get a group. These groups are called the homotopy groups. In the case n = 1, it is also called the fundamental group.
Homotopy category
The idea of homotopy can be turned into a formal category of category theory. The homotopy category is the category whose objects are topological spaces, and whose morphisms are homotopy equivalence classes of continuous maps. Two topological spaces X and Y are isomorphic in this category if and only if they are homotopy-equivalent. Then a functor on the category of topological spaces is homotopy invariant if it can be expressed as a functor on the homotopy category.
For example, homology groups are a functorial homotopy invariant: this means that if f and g from X to Y are homotopic, then the group homomorphisms induced by f and g on the level of homology groups are the same: Hn(f) = Hn(g) : Hn(X) → Hn(Y) for all n. Likewise, if X and Y are in addition path-connected, then the group homomorphisms induced by f and g on the level of homotopy groups are also the same: πn(f) = πn(g) : πn(X) → πn(Y).
Timelike homotopy
On a Lorentzian manifold, certain curves are distinguished as timelike. A timelike homotopy between two timelike curves is a homotopy such that each intermediate curve is timelike. No closed timelike curve (CTC) on a Lorentzian manifold is timelike homotopic to a point (that is, null timelike homotopic); such a manifold is therefore said to be multiply connected by timelike curves. A manifold such as the 3-sphere can be simply connected (by any type of curve), and yet be multiply timelike connected.
Homotopy lifting property
If we have a homotopy ![H\colon X\times [0,1]\to Y](/2009-wikipedia_en_wp1-0.7_2009-05/I/e9541d9e13c03dafcfa9c5d4cbe28677.png) and a cover
and a cover 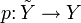 and we are given a map
and we are given a map 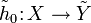 such that
such that 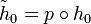 (
( 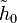 is called a lift of
is called a lift of 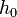 ), then we can lift all of
), then we can lift all of  to a map
to a map ![\tilde H\colon X \times [0,1]\to \tilde Y](/2009-wikipedia_en_wp1-0.7_2009-05/I/1a81492aa96a219203be30bd5f1fe944.png) such that
such that 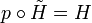 . The homotopy lifting property is used to characterize fibrations.
. The homotopy lifting property is used to characterize fibrations.
Homotopy extension property
Another useful property involving homotopy is the homotopy extension property, which characterizes the extension of a homotopy between two functions from a subset of some set to the set itself. It is useful when dealing with cofibrations.
Isotopy
In case the two given continuous functions f and g from the topological space X to the topological space Y are homeomorphisms, one can ask whether they can be connected 'through homeomorphisms'. This gives rise to the concept of isotopy, which is a homotopy, H, in the notation used before, such that for each fixed t, H(x,t) gives a homeomorphism.
Requiring that two homeomorphisms be isotopic really is a stronger requirement than that they be homotopic. For example, the map of the unit disc in R2 defined by f(x,y) = (−x, −y) is equivalent to a 180-degree rotation around the origin, and so the identity map and f are isotopic because they can be connected by rotations. However, the map on the interval [−1,1] in R defined by f(x) = −x is not isotopic to the identity. Loosely speaking, any homotopy from f to the identity would have to exchange the endpoints, which would mean that they would have to 'pass through' each other. Moreover, f has changed the orientation of the interval, hence it cannot be isotopic to the identity. However, the maps are homotopic; one homotopy from f to the identity is H: [−1,1] × [0,1] → [−1,1] given by H(x,y) = 2yx-x.
In geometric topology—for example in knot theory—the idea of isotopy is used to construct equivalence relations. For example, when should two knots be considered the same? We take two knots, K1 and K2, in three-dimensional space. The intuitive idea of deforming one to the other should correspond to a path of homeomorphisms: an isotopy starting with the identity homeomorphism of three-dimensional space, and ending at a homeomorphism, h, such that h moves K1 to K2. An ambient isotopy, studied in this context, is an isotopy of the larger space, considered in light of its action on the embedded submanifold.
See also
- Mapping class group
- Homeotopy
- Regular homotopy
- Poincaré conjecture