Hexagon

Regular hexagon
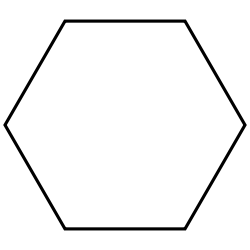A regular hexagon, {6}
Edges and vertices	6
Schläfli symbols	{6} t{3}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D6)
Area (with t=edge length)
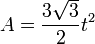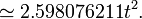Internal angle (degrees)	120°

In geometry, a hexagon is a polygon with six edges and six vertices. A regular hexagon has Schläfli symbol {6}.

Regular hexagon

A regular hexagon is constructible with compass and straightedge. The following is a step-by-step animated method of this, given by Euclid's Elements, Book IV, Proposition 15.

The internal angles of a regular hexagon (one where all sides and all angles are equal) are all 120° and the hexagon has 720 degrees. It has 6 rotational symmetries and 6 reflection symmetries, making up the dihedral group D₆. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice its sides in length. Like squares and equilateral triangles, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons.

The area of a regular hexagon of side length 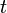is given by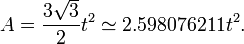

The perimeter of a regular hexagon of side length 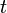is, of course, 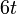, its maximal diameter 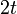, and its minimal diameter .

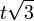There is no platonic solid made of regular hexagons. The archimedean solids with some hexagonal faces are the truncated tetrahedron, truncated octahedron, truncated icosahedron (of soccer ball and fullerene fame), truncated cuboctahedron and the truncated icosidodecahedron.

Related figures

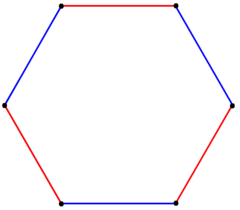A regular hexagon can also be created as a truncated equilateral triangle, with Schläfli symbol t{3}. This form only has D3 symmetry. In this figure, the remaining edges of the original triangle are drawn blue, and new edges from the truncation are red.

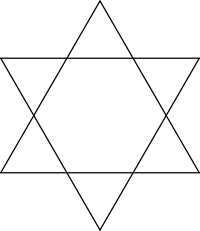The hexagram can be created as a stellation process: extending the 6 edges of a regular hexagon until they meet at 6 new vertices.

Regular and uniform tilings with hexagons

The hexagon can form a regular tessellate the plane with a Schläfli symbol {6,3}, having 3 hexagons around every vertex.	A second hexagonal tessellation of the plane can be formed as a truncated triangular tiling, with one of three hexagons colored differently.	A third tessellation of the plane can be formed with three colored hexagons around every vertex.
Trihexagonal tiling	Trihexagonal tiling
Small rhombitrihexagonal tiling	Great rhombitrihexagonal tiling

Hexagons: natural and human-made

See also

• Hexagram: 6-sided star within a regular hexagon
• Unicursal hexagram: single path, 6-sided star, within a hexagon
• Hexagonal tiling: a regular tiling of hexagons in a plane
• Hexagonal number

External links

• Eric W. Weisstein, Hexagon at MathWorld.
• Definition and properties of a hexagon With interactive animation
• Cassini Images Bizarre Hexagon on Saturn
• Saturn's Strange Hexagon
• A hexagonal feature around Saturn's North Pole
• "Bizarre Hexagon Spotted on Saturn" - from Space.com (27 March 2007)