Green's function
In mathematics, Green's function is a type of function used to solve inhomogeneous differential equations subject to boundary conditions. The term is used in physics, specifically in quantum field theory and statistical field theory, to refer to various types of correlation functions, even those that do not fit the mathematical definition; for this sense, see Correlation function (quantum field theory) and Green's function (many-body theory).
Green's function is named after the British mathematician George Green, who first developed the concept in the 1830s.
Contents |
Definition and uses
Technically, a Green's function, G(x, s), of a linear operator L=L(x) acting on distributions over a subset of Rn, at a point s, is any solution of
where 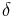 is the Dirac delta function. This technique can be used to solve differential equations of the form;
is the Dirac delta function. This technique can be used to solve differential equations of the form;
If the kernel of L is nontrivial, then the Green's function is not unique. However, in practice, some combination of symmetry, boundary conditions and/or other externally imposed criteria would give us a unique Green's function. Also, Green's functions in general are distributions, not necessarily proper functions.
Green's functions are also a useful tool in condensed matter theory, where they allow the resolution of the diffusion equation, and in quantum mechanics, where the Green's function of the Hamiltonian is a key concept, with important links to the concept of density of states. The Green's functions used in those two domains are highly similar, due to the analogy in the mathematical structure of the diffusion equation and Schrödinger equation. As a side note, the Green's function as used in Physics is usually defined with the opposite sign; that is,
This definition does not significantly change any of the properties of the Green's function.
Motivation
Loosely speaking, if such a function G can be found for the operator L, then if we multiply the equation (1) for the Green's function by f(s), and then perform an integration in the s variable, we obtain;
The right hand side is now given by the equation (2) to be equal to L, thus:
Because the operator L = L(x) is linear and acts on the variable x alone (not on the variable of integration s), we can take the operator L outside of the integration on the right hand side obtaining;
And this implies;
Thus, we can obtain the function u(x) through knowledge of the Green's function in equation (1), and the source term on the right hand side in equation (2). This process has resulted from the linearity of the operator L.
In other words, the solution of equation (2), u(x), can be determined by the integration given in equation (3). Although f(x) is known, this integration cannot be performed unless G is also known. The problem now lies in finding the Green's function G that satisfies equation (1).
Not every operator L admits a Green's function. A Green's function can also be thought of as a right inverse of L. Aside from the difficulties of finding a Green's functions for a particular operator, the integral in equation (3), may be quite difficult to perform. However the method gives a theoretically exact result.
Convolving with a Green's function gives solutions to inhomogeneous differential-integral equations, most commonly a Sturm-Liouville problem. If G is the Green's function of an operator L, then the solution for u of the equation Lu = f is given by
This can be thought of as an expansion of f according to a Dirac delta function basis (projecting f over δ(x − s)) and a superposition of the solution on each projection. Such an integral is known as a Fredholm integral equation, the study of which constitutes Fredholm theory.
Green's function for solving inhomogeneous boundary value problems
The primary use of Green's functions in mathematics is to solve inhomogeneous boundary value problems. In modern theoretical physics, Green's functions are also usually used as propagators in Feynman diagrams (and the phrase "Green's function" is often used for any correlation function).
Framework
Let 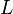 be the Sturm-Liouville operator, a linear differential operator of the form
be the Sturm-Liouville operator, a linear differential operator of the form
and let D be the boundary conditions operator
Let  be a continuous function in
be a continuous function in ![[0,l]](/2009-wikipedia_en_wp1-0.7_2009-05/I/8cf0b3e021d63d93fc5d3146f86cd5c4.png) . We shall also suppose that the problem
. We shall also suppose that the problem
is regular, i.e. only the trivial solution exists for the homogeneous problem.
Theorem
There is one and only one solution u(x) which satisfies
and it is given by
where G(x,s) is Green's function and satisfies the following conditions:
- G(x,s) is continuous in x and s.
- For
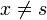 ,
, 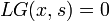 .
. - For
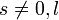 ,
, 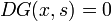 .
. - Derivative "jump":
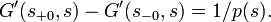
- Symmetry: G(x, s) = G(s, x).
Finding Green's functions
Eigenvalue expansions
If a differential operator L admits a set of eigenvectors 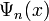 (i.e. a set of functions
(i.e. a set of functions 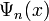 and scalars
and scalars 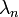 such that
such that 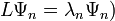 ) that are complete, then we can construct a Green's function from these eigenvectors and eigenvalues.
) that are complete, then we can construct a Green's function from these eigenvectors and eigenvalues.
By complete, we mean that the set of functions :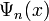 satisfies the following completeness relation:
satisfies the following completeness relation:
We can prove the following:
Now consider applying the operator L to each side of this equation. We end up with the completeness relation, which was assumed true.
The general study of the Green's function written in the above form, and its relationship to the function spaces formed by the eigenvectors, is known as Fredholm theory.
Green's function for the Laplacian
Green's functions for linear differential operators involving the Laplacian may be readily put to use using the second of Green's identities.
To derive Green's theorem, begin with the divergence theorem (otherwise known as Gauss's law):
Let 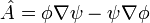 and substitute into Gauss' law. Compute
and substitute into Gauss' law. Compute 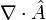 and apply the chain rule for the
and apply the chain rule for the  operator:
operator:
Plugging this into the divergence theorem, we arrive at Green's theorem:
Suppose that our linear differential operator L is the Laplacian, 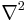 , and that we have a Green's function G for the Laplacian. The defining property of the Green's function still holds:
, and that we have a Green's function G for the Laplacian. The defining property of the Green's function still holds:
Let 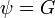 in Green's theorem. We get:
in Green's theorem. We get:
Using this expression, we can solve Laplace's equation 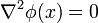 or Poisson's equation
or Poisson's equation 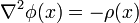 , subject to either Neumann or Dirichlet boundary conditions. In other words, we can solve for
, subject to either Neumann or Dirichlet boundary conditions. In other words, we can solve for 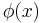 everywhere inside a volume where either (1) the value of
everywhere inside a volume where either (1) the value of 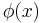 is specified on the bounding surface of the volume (Dirichlet boundary conditions), or (2) the normal derivative of
is specified on the bounding surface of the volume (Dirichlet boundary conditions), or (2) the normal derivative of 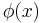 is specified on the bounding surface (Neumann boundary conditions).
is specified on the bounding surface (Neumann boundary conditions).
Suppose we're interested in solving for 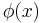 inside the region. Then the integral
inside the region. Then the integral
reduces to simply 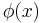 due to the defining property of the Dirac delta function and we have:
due to the defining property of the Dirac delta function and we have:
This form expresses the well-known property of harmonic functions that if the value or normal derivative is known on a bounding surface, then the value of the function inside the volume is known everywhere.
In electrostatics, we interpret 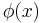 as the electric potential,
as the electric potential, 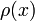 as electric charge density, and the normal derivative
as electric charge density, and the normal derivative 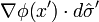 as the normal component of the electric field.
as the normal component of the electric field.
If we're interested in solving a Dirichlet boundary value problem, we choose our Green's function such that 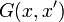 vanishes when either x or x' is on the bounding surface; conversely, if we're interested in solving a Neumann boundary value problem, we choose our Green's function such that its normal derivative vanishes on the bounding surface. Thus we are left with only one of the two terms in the surface integral.
vanishes when either x or x' is on the bounding surface; conversely, if we're interested in solving a Neumann boundary value problem, we choose our Green's function such that its normal derivative vanishes on the bounding surface. Thus we are left with only one of the two terms in the surface integral.
With no boundary conditions, the Green's function for the Laplacian (Green's function for the three-variable Laplace equation) is:
Supposing that our bounding surface goes out to infinity, and plugging in this expression for the Green's function, we arrive at the familiar expression for electric potential in terms of electric charge density (in the CGS unit system) as
Example
Given the problem
Find Green's function.
First step: The Green's function for the linear operator at hand is defined as the solution to
If 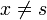 , then the delta function gives zero, and the general solution is
, then the delta function gives zero, and the general solution is
For 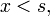 the boundary condition at
the boundary condition at 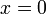 implies
implies
The equation of 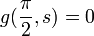 is skipped because
is skipped because 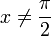 if
if 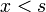 and
and 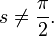
For 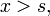 the boundary condition at
the boundary condition at 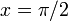 implies
implies
The equation of 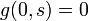 is skipped for similar reasons.
is skipped for similar reasons.
To summarize the results thus far:
Second step: Now we shall determine  and
and 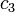 .
.
Ensuring continuity in the Green's function at 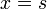 implies
implies
One can also ensure proper discontinuity in the first derivative by integrating the defining differential equation from 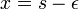 to
to 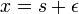 and taking the limit as
and taking the limit as 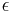 goes to zero:
goes to zero:
The two (dis)continuity equations can be solved for  and
and 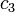 to obtain
to obtain
So our Green's function for this problem is:
Further examples
- Let n=1 and let the subset be all of R. Let L be d/dx. Then, the Heaviside step function H(x − x0) is a Green's function of L at x0.
- Let n=2 and let the subset be the quarter-plane { (x, y) : x, y ≥ 0 } and L be the Laplacian. Also, assume a Dirichlet boundary condition is imposed at x = 0 and a Neumann boundary condition is imposed at y = 0. Then the Green's function is
See also
- Discrete Green's functions can be defined on graphs and grids.
- Impulse response
- Green's identities
References
- Eyges, Leonard, The Classical Electromagnetic Field, Dover Publications, New York, 1972. ISBN 0-486-63947-9. (Chapter 5 contains a very readable account of using Green's functions to solve boundary value problems in electrostatics.)
- A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
- A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9
External links
- Eric W. Weisstein, Green's Function at MathWorld.
- Green's function for differential operator at PlanetMath.
- Green's function on PlanetMath
- GreenFunctionsAndConformalMapping on PlanetMath
- Tutorial on Green's function
- Boundary Element Method (for some idea on how Green's function may be used with the boundary element method for solving potential problems numerically)
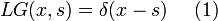
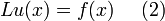
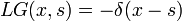
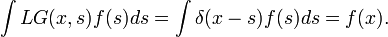
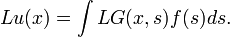
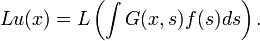
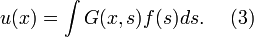
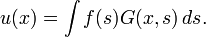
![L = {d \over dx}\left[ p(x) {d \over dx} \right] + q(x)](/2009-wikipedia_en_wp1-0.7_2009-05/I/27c569c3fe145a50d74fab3caa8c311f.png)
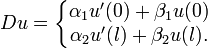
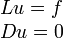
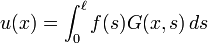
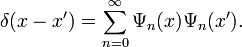
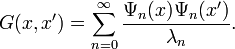
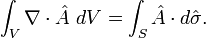
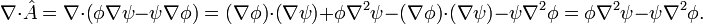
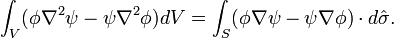
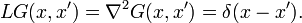
![\int_V \phi(x') \delta(x - x') - G(x,x') \nabla^2\phi(x')\ d^3x' = \int_S \left[\phi(x')\nabla' G(x,x') - G(x,x')\nabla'\phi(x')\right] \cdot d\hat\sigma'](/2009-wikipedia_en_wp1-0.7_2009-05/I/84d9ec2da66b899b49f2fe950d56b78b.png)
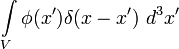
![\phi(x) = \int_V G(x,x') \rho(x')\ d^3x' + \int_S \left[\phi(x')\nabla' G(x,x') - G(x,x')\nabla'\phi(x')\right] \cdot d\hat\sigma'.](/2009-wikipedia_en_wp1-0.7_2009-05/I/f00be7f0acad38e891e29a61e1feaca1.png)
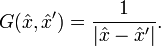
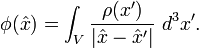
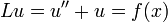
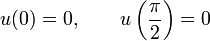
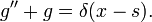
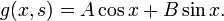
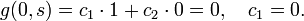
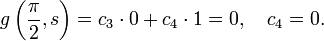
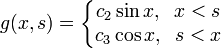
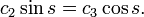
![c_3 \cdot [ - \sin s ] - c_2 \cdot \cos s = 1\, .](/2009-wikipedia_en_wp1-0.7_2009-05/I/43a119e34263e55e00abfbe114d16f09.png)
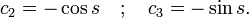
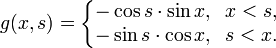
![G(x, y, x_0, y_0)=\frac{1}{2\pi}\left[\ln\sqrt{(x-x_0)^2+(y-y_0)^2}-\ln\sqrt{(x+x_0)^2+(y-y_0)^2}\right]](/2009-wikipedia_en_wp1-0.7_2009-05/I/43f0907f206c556734c7c09d58bdd939.png)
![+\frac{1}{2\pi}\left[\ln\sqrt{(x-x_0)^2+(y+y_0)^2}-\ln\sqrt{(x+x_0)^2+(y+y_0)^2}\right].](/2009-wikipedia_en_wp1-0.7_2009-05/I/1a6743e41c576ca387a97a856cf25711.png)