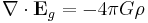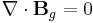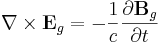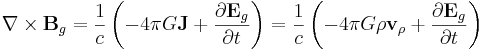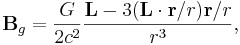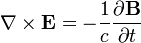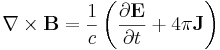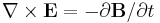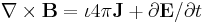Gravitomagnetism
Gravitomagnetism (sometimes Gravitoelectromagnetism, abbreviated GEM), refers to a set of formal analogies between Maxwell's field equations and an approximation to the Einstein field equations for general relativity, valid under certain conditions. For instance, the most common version of GEM is valid only far from isolated sources, and for slowly moving test particles.
Contents[hide] |
Background
This approximate reformulation of gravitation as described by general relativity makes a "fictitious force" appear in a frame of reference different from a moving, gravitating body. By analogy with electromagnetism, this fictitious force is called the gravitomagnetic force, since it arises in the same way that a moving electric charge creates a magnetic field, the analogous "fictitious force" in special relativity. The main consequence of the gravitomagnetic force, or acceleration, is that a free-falling object near a massive rotating object will itself rotate. This prediction, often loosely referred to as a gravitomagnetic effect, is among the last basic predictions of general relativity yet to be directly tested.
Indirect validations of gravitomagnetic effects have been derived from analyses of relativistic jets. Sir Roger Penrose had proposed a frame dragging mechanism for extracting energy and momentum from rotating black holes.[1] Reva Kay Williams, University of Florida, developed a rigorous proof that validated Penrose's mechanism.[2] Her model showed the Lense-Thirring effect could account for the observed high energies and luminosities of quasars and active galactic nuclei; the collimated jets about their polar axis; and the asymmetrical jets (relative to the orbital plane).[3] All of those observed properties could be explained in terms of gravitomagnetic effects.[4] Williams’ application of Penrose’s mechanism can be applied to black holes of any size.[5] Subsequently, relativistic jets can serve as the largest and brightest form of validations for gravitomagnetism.
A group at Stanford University is currently analyzing data from the first direct test of GEM, the Gravity Probe B satellite experiment.
Equations
According to general relativity, the gravitational field produced by a rotating object (or any rotating mass-energy) can, in a particular limiting case, be described by equations that have the same form as the magnetic field in classical electromagnetism. Starting from the basic equation of general relativity, the Einstein field equation, and assuming a weak gravitational field or reasonably flat spacetime, Lano, [6] Fedosin [7] Agop, Buzea and Ciobanu, [8] Mashhoon, Gronwald, and Lichtenegger,[9] and Clark and Tucker,[10] have derived the following gravitational analogs to Maxwell's equations for electromagnetism, called the "GEM equations":
where:
- Eg is the static gravitational field (conventional gravity, also called gravitoelectric for the sake of analogy);
- Bg is the gravitomagnetic field;
- ρ is mass density (instead of electric charge density);
- vρ is the velocity of the mass flow generating the gravitomagnetic field;
- J is mass current density (J = ρ vρ);
- G is the gravitational constant;
- c is the speed of propagation of gravity (equal to, by general relativity, the speed of light).
For a test particle whose mass m is "small," the net (Lorentz) force acting on it due to a GEM field is described by the following GEM analog to the Lorentz force equation:
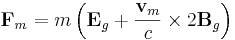 .
.
where:
In the literature, all instances of Bg in the GEM equations are multiplied by 1/2, a factor absent from Maxwell's equations. This factor vanishes if Bg in the GEM version of the Lorentz force equation is multiplied by 2, as shown above. The factors 2 and 1/2 arise because the effective gravitomagnetic charge is twice the static gravitational (gravitoelectric) charge, a remnant of the spin-2 character of the gravitational field. For a pure spin-1 field such as the genuine electromagnetic field, the magnetic charge equals the electric charge.
For the field Bg near a rotating body from GEM equations follows:
where L is the angular momentum of the body.
Comparison with electromagnetism
The above GEM equations are very similar to Maxwell's equations in free space, which in cgs units are:
Adopting Planck units eliminates G and c from both sets of equations by normalizing these constants to 1. The two sets of equations are now identical but for the minus sign preceding 4π in the GEM equations. These two minus signs stem from an essential difference between gravity and electromagnetism: electrostatic charges of identical sign repel each other, while two like signed (positive) masses attract each other. Hence the GEM equations are simply Maxwell's equations with mass (or mass density) substituting for charge (or charge density), and -G replacing the Coulomb force constant 1/(4πε0). The following Table summarizes the results thus far:
| Common Structure of the Maxwell and GEM Equations Given Planck units. |
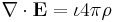
ι = 1 (Maxwell) or -1 (GEM). |
The factor of 4π remains in both the GEM and Maxwell's equations because G and 1/(4πε0) are normalized to 1, and not 4πG and ε0.
Higher-order effects
Some higher-order gravitomagnetic effects can reproduce effects reminiscent of the interactions of more conventional polarized charges. For instance, if two wheels are spun on a common axis, the mutual gravitational attraction between the two wheels arguably ought to be greater if they spin in opposite directions than in the same direction. This can be expressed as an attractive or repulsive gravitomagnetic component.
Gravitomagnetic arguments also predict that a flexible or fluid toroidal mass undergoing minor axis rotation ("smoke ring" rotation) will tend to pull matter preferentially in through one throat and expel it from the other (a case of rotational frame dragging, acting through the throat). In theory, this configuration might be used for accelerating objects (through the throat) without such objects experiencing any g-forces.[11]
Consider a toroidal mass with two degrees of rotation (both major axis and minor-axis spin, both turning inside out and revolving). This represents a "special case" in which gravitomagnetic effects generate a chiral corkscrew-like gravitational field around the object. The reaction forces to dragging at the inner and outer equators would normally be expected to be equal and opposite in magnitude and direction respectively in the simpler case involving only minor-axis spin. When both rotations are applied simultaneously, these two sets of reaction forces can be said to occur at different depths in a radial Coriolis field that extends across the rotating torus, making it more difficult to establish that cancellation is complete.
Modelling this complex behaviour as a curved spacetime problem has yet to be done and is believed very difficult.
Gravitomagnetic field of Earth
- Bg, Earth = 10−14 rad·s−1[12]
See the Gravity Probe B experiment.
Fringe physics
Incomplete understanding of the meaning of the similarity of the gravitomagnetic formulas, above, and Maxwell's equations for (real) electricity and magnetism have given rise to fringe physics. Use of the gravitomagnetic analogy for a simplified form of the Einstein field equations, on the other hand, is firmly part of General Relativity. It is an approximation to the current standard theory of gravitation, and has testable predictions, which are in the final stages of being directly tested by the Gravity Probe B experiment. Despite the use of the word magnetism in gravitomagnetism, and despite the similarity of the GEM force laws to the (real) electromagnetic force law, gravitomagnetism should not be confused with any of the following:
- Claims to have constructed anti-gravity devices;
- Eugene Podkletnov's claims to have constructed gravity-shielding devices and gravitational reflection beams.
- Any proposal to produce gravitation using electrical circuits.
See also
- Anti-gravity
- Geodetic effect
- Gravitational radiation
- Gravity Probe B
- Frame-dragging
References
- ↑ Penrose, R. (1969). Gravitational collapse: The role of general relativity. Nuovo Cimento Rivista, Numero Speciale 1, 252-276.
- ↑ Williams, R. K. (1995, May 15). Extracting x rays, Ύ rays, and relativistic e-e+ pairs from supermassive Kerr black holes using the Penrose mechanism. Physical Review, 51(10), 5387-5427.
- ↑ Williams, R. K. (2004, August 20). Collimated escaping vortical polar e-e+ jets intrinsically produced by rotating black holes and Penrose processes. The Astrophysical Journal, 611, 952-963.
- ↑ Williams, R. K. (2005). Gravitomagnetic field and Penrose scattering processes. Annals of the New York Academy of Sciences, 1045, 232-245.
- ↑ Williams, R. K. (2001, October 15). Collimated energy-momentum extraction from rotating black holes in quasars and microquasars using the Penrose mechanism. AIP Conference Proceedings, 586, 448-453. (http://arxiv.org/abs/astro-ph/0111161)
- ↑ R.P. Lano (1996-03-12). "Gravitational Meissner Effect". arXiv: hep-th 9603077. http://arxiv.org/abs/hep-th/9603077.
- ↑ Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, (1999-06-09) 544 pp. ISBN 5-8131-0012-1. [1],
- ↑ M. Agop, C. Gh. Buzea and B. Ciobanu (1999-11-10). "On Gravitational Shielding in Electromagnetic Fields.". arXiv: physics 9911011. http://arxiv.org/abs/physics/9911011.
- ↑ Mashhoon, Gronwald, Lichtenegger (1999-12-08). "Gravitomagnetism and the Clock Effect". arXiv:General Relativity and Quantum Cosmology 9912027. http://arxiv.org/abs/gr-qc/9912027.
- ↑ http://www.iop.org/EJ/article/0264-9381/17/19/311/q01911.pdf
- ↑ Forward, R.L. 1963. Guidelines to Antigravity. American Journal of Physics. 31: 166-170
- ↑ "Experimental Detection of the Gravitomagnetic London Moment" by Martin Tajmar, Florin Plesescu, Klaus Marhold & Clovis J. de Matos
Further reading
- Clark, S J; R W Tucker (2000). "Gauge symmetry and gravito-electromagnetism" (subscription required). Class. Quantum Grav. 17: 4125–4157. doi:. http://www.iop.org/EJ/article/0264-9381/17/19/311/q01911.pdf.
- Forward, Robert L. (1963). "Guidelines to antigravity". American Journal of Physics 31 (3): 166–170. doi:.
- Jantzen, Robert T.; Carini, Paolo; and Bini, Donato (1992). "The Many Faces of Gravitoelectromagnetism". Ann. Physics 215: 1–50. doi:. eprint version
- Mashhoon, Bahram (2000). "Gravitoelectromagnetism". arΧiv: gr-qc/0011014
- Mashhoon, Bahram (2003). "Gravitoelectromagnetism: a Brief Review". arΧiv: gr-qc/0311030 In: Iorio, L. (Ed.), Measuring Gravitomagnetism: A Challenging Enterprise, Nova Publishers, Hauppauge (NY), pp. 29-39, 2007. A recent introduction to GEM by a leading expert.
- Tajmar, M.; and de Matos, C. J. (2001). "Gravitomagnetic Barnett Effect". Indian J.Phys. B 75: 459–461. arΧiv:gr-qc/0012091.
- Wheeler, John Archibald (1990). "Gravity's next prize: Gravitomagnetism". A journey into gravity and spacetime. New York: Scientific American Library. pp. 232-233. ISBN 0716750163.
- Iorio, Lorenzo (2007). Measuring Gravitomagnetism: A Challenging Enterprise. Hauppaugem NY: Nova Publishers. ISBN 1600210023.
- Jefimenko, Oleg D. (1992). Causality, electromagnetic induction, and gravitation : a different approach to the theory of electromagnetic and gravitational fields. Star City, West Virginia: Electret Scientific. ISBN 0917406095.
- Heaviside, Oliver, "A gravitational and electromagnetic analogy". The Electrician, 1893.
External links
- Gyroscopic Superconducting Gravitomagnetic Effectsnews on tentative result of European Space Agency (esa) research
- In Search of gravitomagnetism, NASA, 20 April 2004.
- Gravitomagnetic London Moment-New test of General Relativity?
- Measurement of Gravitomagnetic and Acceleration Fields Around Rotating Superconductors M. Tajmar, et al., 17 October 2006.
- Test of the Lense-Thirring effect with the MGS Mars probe, New Scientist, January 2007.
|
|||||||||