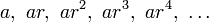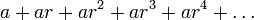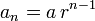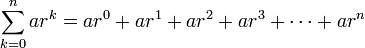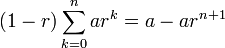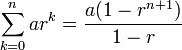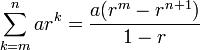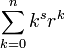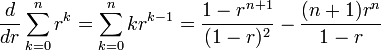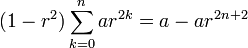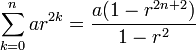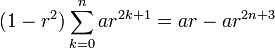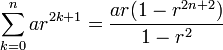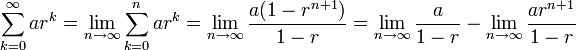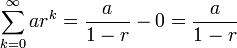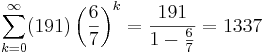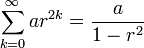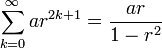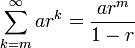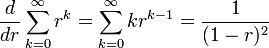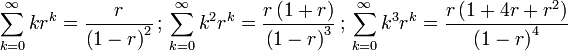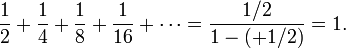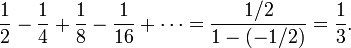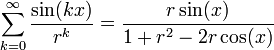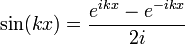Geometric progression

In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2. The sum of the terms of a geometric progression is known as a geometric series.
Thus, the general form of a geometric sequence is
and that of a geometric series is
where r ≠ 0 is the common ratio and a is a scale factor, equal to the sequence's start value.
Contents |
Elementary properties
The n-th term of a geometric sequence with initial value a and common ratio r is given by
Such a geometric sequence also follows the recursive relation
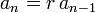 for every integer
for every integer 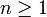
Generally, to check whether a given sequence is geometric, one simply checks whether successive entries in the sequence all have the same ratio.
The common ratio of a geometric series may be negative, resulting in an alternating sequence, with numbers switching from positive to negative and back. For instance
- 1, -3, 9, -27, 81, -243, ...
is a geometric sequence with common ratio -3.
The behaviour of a geometric sequence depends on the value of the common ratio.
If the common ratio is:
- Positive, the terms will all be the same sign as the initial term.
- Negative, the terms will alternate between positive and negative.
- Greater than 1, there will be exponential growth towards positive infinity.
- 1, the progression is a constant sequence.
- Between -1 and 1 but not zero, there will be exponential decay towards zero.
- −1, the progression is an alternating sequence (see alternating series)
- Less than −1, for the absolute values there is exponential growth towards infinity.
Geometric sequences (with common ratio not equal to -1,1 or 0) show exponential growth or exponential decay, as opposed to the Linear growth (or decline) of an arithmetic progression such as 4, 15, 26, 37, 48, ... (with common difference 11). This result was taken by T.R. Malthus as the mathematical foundation of his Principle of Population. Note that the two kinds of progression are related: exponentiating each term of an arithmetic progression yields a geometric progression, while taking the logarithm of each term in a geometric progression with a positive common ratio yields an arithmetic progression.
Geometric series
A geometric series is the sum of the numbers in a geometric progression:
We can find a simpler formula for this sum by multiplying both sides of the above equation by 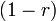 , and we'll see that
, and we'll see that
since all the other terms cancel. Rearranging (for 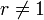 ) gives the convenient formula for a geometric series:
) gives the convenient formula for a geometric series:
Note: If one were to begin the sum not from 0, but from a higher term, say m, then
Differentiating this formula with respect to r allows us to arrive at formulae for sums of the form
For example:
For a geometric series containing only even powers of  multiply by
multiply by 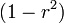 :
:
Then
For a series with only odd powers of 
and
Infinite geometric series
An infinite geometric series is an infinite series whose successive terms have a common ratio. Such a series converges if and only if the absolute value of the common ratio is less than one ( | r | < 1 ). Its value can then be computed from the finite sum formulae
Since:
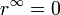 (when | r |<1).
(when | r |<1).
Then:
For example, using numerical values
For a series containing only even powers of  ,
,
and for odd powers only,
In cases where the sum does not start at k = 0,
Above formulae are valid only for | r | < 1. The latter formula is actually valid in every Banach algebra, as long as the norm of r is less than one, and also in the field of p-adic numbers if | r |p < 1. As in the case for a finite sum, we can differentiate to calculate formulae for related sums. For example,
This formula only works for | r | < 1 as well. From this, it follows that, for | r | < 1,
Also, the infinite series 1/2 + 1/4 + 1/8 + 1/16 + · · · is an elementary example of a series that converges absolutely.
It is a geometric series whose first term is 1/2 and whose common ratio is 1/2, so its sum is
The inverse of the above series is 1/2 − 1/4 + 1/8 − 1/16 + · · · is a simple example of an alternating series that converges absolutely.
It is a geometric series whose first term is 1/2 and whose common ratio is −1/2, so its sum is
Complex numbers
The summation formula for geometric series remains valid even when the common ratio is a complex number. This fact can be used to calculate some sums of non-obvious geometric series, such as:
The proof of this formula starts with
a consequence of Euler's formula. Substituting this into the series above, we get
![\sum_{k=0}^{\infty} \frac{\sin(kx)}{r^k} = \frac{1}{2 i} \left[ \sum_{k=0}^{\infty} \left( \frac{e^{ix}}{r} \right)^k - \sum_{k=0}^{\infty} \left(\frac{e^{-ix}}{r}\right)^k\right]](/2009-wikipedia_en_wp1-0.7_2009-05/I/01d16a5c8bb41faa7586204860d2324b.png) .
.
This is just the difference of two geometric series. From here, it is then a straightforward application of our formula for infinite geometric series to finish the proof.
Product
The product of a geometric progression is the product of all terms. If all terms are positive, then it can be quickly computed by taking the geometric mean of the progression's first and last term, and raising that mean to the power given by the number of terms. (This is very similar to the formula for the sum of terms of an arithmetic sequence: take the arithmetic mean of the first and last term and multiply with the number of terms.)
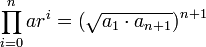 (if
(if 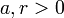 ).
).
Proof:
Let the product be represented by P:
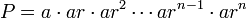 .
.
Now, carrying out the multiplications, we conclude that
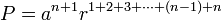 .
.
Applying the sum of arithmetic series, the expression will yield
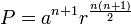 .
.
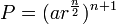 .
.
We raise both sides to the second power:
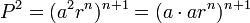 .
.
Consequently
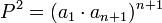 and
and
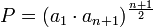 ,
,
which concludes the proof.
Relationship to geometry and Euclid's work
Books VIII and IX of Euclid's Elements analyze geometric progressions and give several of their properties.
A geometric progression gains its geometric character from the fact that the areas of two geometrically similar plane figures are in "duplicate" ratio to their corresponding sides; further the volumes of two similar solid figures are in "triplicate" ratio of their corresponding sides.
The meaning of the words "duplicate" and "triplicate" in the previous paragraph is illustrated by the following examples. Given two squares whose sides have the ratio 2 to 3, then their areas will have the ratio 4 to 9; we can write this as 4 to 6 to 9 and notice that the ratios 4 to 6 and 6 to 9 both equal 2 to 3; so by using the side ratio 2 to 3 "in duplicate" we obtain the ratio 4 to 9 of the areas, and the sequence 4, 6, 9 is a geometric sequence with common ratio 3/2. Similarly, give two cubes whose side ratio is 2 to 5, their volume ratio is 8 to 125, which can be obtained as 8 to 20 to 50 to 125, the original ratio 2 to 5 "in triplicate", yielding a geometric sequence with common ration 5/2.
Elements, Book IX
The geometric progression 1, 2, 4, 8, 16, 32, ... (or, in the binary numeral system, 1, 10, 100, 1000, 10000, 100000, ... ) is important in number theory. Book IX, Proposition 36 of Elements proves that if the sum of the first n terms of this progression is a prime number, then this sum times the nth term is a perfect number. For example, the sum of the first 5 terms of the series (1 + 2 + 4 + 8 + 16) is 31, which is a prime number. The sum 31 multiplied by 16 (the 5th term in the series) equals 496, which is a perfect number.
Book IX, Proposition 35 proves that in a geometric series if the first term is subtracted from the second and last term in the sequence then as the excess of the second is to the first, so will the excess of the last be to all of those before it. (This is a restatement of our formula for geometric series from above.) Applying this to the geometric progression 31,62,124,248,496 (which results from 1,2,4,8,16 by multiplying all terms by 31), we see that 62 minus 31 is to 31 as 496 minus 31 is to the sum of 31,62,124,248. Therefore the numbers 1,2,4,8,16,31,62,124,248 add up to 496 and further these are all the numbers which divide 496. For suppose that P divides 496 and it is not amongst these numbers. Assume P×Q equals 16×31, or 31 is to Q as P is to 16. Now P cannot divide 16 or it would be amongst the numbers 1,2,4,8,16. Therefore 31 cannot divide Q. And since 31 does not divide Q and Q measures 496, the fundamental theorem of arithmetic implies that Q must divide 16 and be amongst the numbers 1,2,4,8,16. Let Q be 4, then P must be 124, which is impossible since by hypothesis P is not amongst the numbers 1,2,4,8,16,31,62,124,248.
See also
- Arithmetic progression
- Exponential function
- Harmonic series
- Infinite series
- Thomas Robert Malthus
- Hackenbush
External Link
References
- Hall & Knight, Higher Algebra, p. 39, ISBN 81-8116-000-2
- Eric W. Weisstein, Geometric Series at MathWorld.