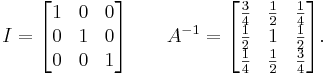Gauss–Jordan elimination
In linear algebra, Gauss–Jordan elimination is a version of Gaussian elimination that puts zeros both above and below each pivot element as it goes from the top row of the given matrix to the bottom. In other words, Gauss-Jordan elimination brings a matrix to reduced row echelon form, whereas Gaussian elimination takes it only as far as row echelon form. Every matrix has a reduced row echelon form, and this algorithm is guaranteed to produce it.
Gauss–Jordan elimination is considerably less efficient than Gaussian elimination with backsubstitution when solving a system of linear equations. However, it is well suited for calculating the matrix inverse.
It is named in honor of Carl Friedrich Gauss and Wilhelm Jordan.
Application to finding inverses
If Gauss–Jordan elimination is applied on a square matrix, it can be used to calculate the matrix's inverse. This can be done by augmenting the square matrix with the identity matrix of the same dimensions, and through the following matrix operations:
If the original square matrix, 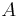 , is given by the following expression:
, is given by the following expression:
Then, after augmenting by the identity, the following is obtained:
By performing elementary row operations on the ![[ A I ]](/2009-wikipedia_en_wp1-0.7_2009-05/I/fedcec8bfd1708c7201ba7e92ca7bc55.png) matrix until
matrix until 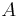 reaches reduced row echelon form, the following is the final result:
reaches reduced row echelon form, the following is the final result:
The matrix augmentation can now be undone, which gives the following:
A matrix is non-singular (meaning that it has an inverse matrix) iff the identity matrix can be obtained using only elementary row operations.
References
- Lipschutz, Seymour, and Lipson, Mark. "Schaum's Outlines: Linear Algebra". Tata McGraw-hill edition. Delhi 2001. pp. 69-80.
- Strang, Gilbert (2003). Introduction to Linear Algebra (3rd edition ed.). Wellesley, Massachusetts: Wellesley-Cambridge Press. pp. 74-76.
External links
- Algorithm for Gauss-Jordan elimination in Matlab
- Algorithm for Gauss-Jordan elimination in Python
- An online tool solve nxm linear systems using Gauss-Jordan elimination (source-code and mobile version included), by Felipe Santos de Andrade (Spanish)
- Algorithm for Gauss-Jordan elimination in Basic
- Module for Gauss-Jordan Elimination
- Example of Gauss-Jordan Elimination "Step-by-Step"
![[ A I ] \Longrightarrow
A^{-1} [ A I ] \Longrightarrow
[ I A^{-1} ].](/2009-wikipedia_en_wp1-0.7_2009-05/I/6e91cc5ed5557ae6465772f2cb304853.png)
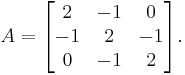
![[ A I ] =
\begin{bmatrix}
2 & -1 & 0 & 1 & 0 & 0\\
-1 & 2 & -1 & 0 & 1 & 0\\
0 & -1 & 2 & 0 & 0 & 1
\end{bmatrix}.](/2009-wikipedia_en_wp1-0.7_2009-05/I/ea66fd6076141f91f2cefd5216476dc3.png)
![[ I A^{-1} ] =
\begin{bmatrix}
1 & 0 & 0 & \frac{3}{4} & \frac{1}{2} & \frac{1}{4}\\
0 & 1 & 0 & \frac{1}{2} & 1 & \frac{1}{2}\\
0 & 0 & 1 & \frac{1}{4} & \frac{1}{2} & \frac{3}{4}
\end{bmatrix}.](/2009-wikipedia_en_wp1-0.7_2009-05/I/c1f426136c1c5a58f57b5e2b66060f05.png)