Fractal

The Mandelbrot set is a famous example of a fractal.

A closer view of the Mandelbrot set.

A fractal is generally "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole,"^[1] a property called self-similarity. The term was coined by Benoît Mandelbrot in 1975 and was derived from the Latin fractus meaning "broken" or "fractured." A mathematical fractal is based on an equation that undergoes iteration, a form of feedback based on recursion.^[2]

A fractal often has the following features:^[3]

• It has a fine structure at arbitrarily small scales.
• It is too irregular to be easily described in traditional Euclidean geometric language.
• It is self-similar (at least approximately or stochastically).
• It has a Hausdorff dimension which is greater than its topological dimension (although this requirement is not met by space-filling curves such as the Hilbert curve).
• It has a simple and recursive definition.

Because they appear similar at all levels of magnification, fractals are often considered to be infinitely complex (in informal terms). Natural objects that approximate fractals to a degree include clouds, mountain ranges, lightning bolts, coastlines, and snow flakes. However, not all self-similar objects are fractals—for example, the real line (a straight Euclidean line) is formally self-similar but fails to have other fractal characteristics; for instance, it is regular enough to be described in Euclidean terms.

Images of fractals can be created using fractal generating software. Images produced by such software are normally referred to as being fractals even if they do not have the above characteristics, as it is quite possible to zoom into a region of the image that does not exhibit any fractal properties.

History

Animated construction of a Sierpiński Triangle, only going nine generations of infinite—click for larger image.

To create a Koch snowflake, one begins with an equilateral triangle and then replaces the middle third of every line segment with a pair of line segments that form an equilateral "bump." One then performs the same replacement on every line segment of the resulting shape, ad infinitum. With every iteration, the perimeter of this shape increases by one third of the previous length. The Koch snowflake is the result of an infinite number of these iterations, and has an infinite length, while its area remains finite. For this reason, the Koch snowflake and similar constructions were sometimes called "monster curves."

The mathematics behind fractals began to take shape in the 17th century when mathematician and philosopher Leibniz considered recursive self-similarity (although he made the mistake of thinking that only the straight line was self-similar in this sense).

It took until 1872 before a function appeared whose graph would today be considered fractal, when Karl Weierstrass gave an example of a function with the non-intuitive property of being everywhere continuous but nowhere differentiable. In 1904, Helge von Koch, dissatisfied with Weierstrass's very abstract and analytic definition, gave a more geometric definition of a similar function, which is now called the Koch snowflake. In 1915, Waclaw Sierpinski constructed his triangle and, one year later, his carpet. Originally these geometric fractals were described as curves rather than the 2D shapes that they are known as in their modern constructions. In 1918, Bertrand Russell had recognised a "supreme beauty" within the mathematics of fractals that was then emerging.^[2] The idea of self-similar curves was taken further by Paul Pierre Lévy, who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole described a new fractal curve, the Lévy C curve. Georg Cantor also gave examples of subsets of the real line with unusual properties—these Cantor sets are also now recognized as fractals.

Iterated functions in the complex plane were investigated in the late 19th and early 20th centuries by Henri Poincaré, Felix Klein, Pierre Fatou and Gaston Julia. However, without the aid of modern computer graphics, they lacked the means to visualize the beauty of many of the objects that they had discovered.

In the 1960s, Benoît Mandelbrot started investigating self-similarity in papers such as How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension, which built on earlier work by Lewis Fry Richardson. Finally, in 1975 Mandelbrot coined the word "fractal" to denote an object whose Hausdorff-Besicovitch dimension is greater than its topological dimension. He illustrated this mathematical definition with striking computer-constructed visualizations. These images captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".

Examples

A Julia set, a fractal related to the Mandelbrot set

A class of examples is given by the Cantor sets, Sierpinski triangle and carpet, Menger sponge, dragon curve, space-filling curve, and Koch curve. Additional examples of fractals include the Lyapunov fractal and the limit sets of Kleinian groups. Fractals can be deterministic (all the above) or stochastic (that is, non-deterministic). For example, the trajectories of the Brownian motion in the plane have a Hausdorff dimension of 2.

Chaotic dynamical systems are sometimes associated with fractals. Objects in the phase space of a dynamical system can be fractals (see attractor). Objects in the parameter space for a family of systems may be fractal as well. An interesting example is the Mandelbrot set. This set contains whole discs, so it has a Hausdorff dimension equal to its topological dimension of 2—but what is truly surprising is that the boundary of the Mandelbrot set also has a Hausdorff dimension of 2 (while the topological dimension of 1), a result proved by Mitsuhiro Shishikura in 1991. A closely related fractal is the Julia set.

Generating fractals

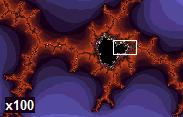Even 2000 times magnification of the Mandelbrot set uncovers fine detail resembling the full set.

Four common techniques for generating fractals are:

• Escape-time fractals — (also known as "orbits" fractals) These are defined by a formula or recurrence relation at each point in a space (such as the complex plane). Examples of this type are the Mandelbrot set, Julia set, the Burning Ship fractal, the Nova fractal and the Lyapunov fractal. The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly.
• Iterated function systems — These have a fixed geometric replacement rule. Cantor set, Sierpinski carpet, Sierpinski gasket, Peano curve, Koch snowflake, Harter-Heighway dragon curve, T-Square, Menger sponge, are some examples of such fractals.
• Random fractals — Generated by stochastic rather than deterministic processes, for example, trajectories of the Brownian motion, Lévy flight, fractal landscapes and the Brownian tree. The latter yields so-called mass- or dendritic fractals, for example, diffusion-limited aggregation or reaction-limited aggregation clusters.
• Strange attractors — Generated by iteration of a map or the solution of a system of initial-value differential equations that exhibit chaos.

Classification

Fractals can also be classified according to their self-similarity. There are three types of self-similarity found in fractals:

• Exact self-similarity — This is the strongest type of self-similarity; the fractal appears identical at different scales. Fractals defined by iterated function systems often display exact self-similarity.
• Quasi-self-similarity — This is a loose form of self-similarity; the fractal appears approximately (but not exactly) identical at different scales. Quasi-self-similar fractals contain small copies of the entire fractal in distorted and degenerate forms. Fractals defined by recurrence relations are usually quasi-self-similar but not exactly self-similar.
• Statistical self-similarity — This is the weakest type of self-similarity; the fractal has numerical or statistical measures which are preserved across scales. Most reasonable definitions of "fractal" trivially imply some form of statistical self-similarity. (Fractal dimension itself is a numerical measure which is preserved across scales.) Random fractals are examples of fractals which are statistically self-similar, but neither exactly nor quasi-self-similar.

In nature

Approximate fractals are easily found in nature. These objects display self-similar structure over an extended, but finite, scale range. Examples include clouds, snow flakes, crystals, mountain ranges, lightning, river networks, cauliflower or broccoli, and systems of blood vessels and pulmonary vessels. Coastlines may be loosely considered fractal in nature.

Trees and ferns are fractal in nature and can be modeled on a computer by using a recursive algorithm. This recursive nature is obvious in these examples — a branch from a tree or a frond from a fern is a miniature replica of the whole: not identical, but similar in nature. The connection between fractals and leaves are currently being used to determine how much carbon is really contained in trees. This connection is hoped to help determine and solve the environmental issue of carbon emission and control. ^[4]

In 1999, certain self similar fractal shapes were shown to have a property of "frequency invariance" — the same electromagnetic properties no matter what the frequency — from Maxwell's equations (see fractal antenna).^[5]

In creative works

Further information: Fractal art

Fractal patterns have been found in the paintings of American artist Jackson Pollock. While Pollock's paintings appear to be composed of chaotic dripping and splattering, computer analysis has found fractal patterns in his work.^[6]

Decalcomania, a technique used by artists such as Max Ernst, can produce fractal-like patterns.^[7] It involves pressing paint between two surfaces and pulling them apart.

Fractals are also prevalent in African art and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles.^[8]

Applications

Main article: Fractal analysis

As described above, random fractals can be used to describe many highly irregular real-world objects. Other applications of fractals include:^[10]

• Classification of histopathology slides in medicine
• Fractal landscape or Coastline complexity
• Enzyme/enzymology (Michaelis-Menten kinetics)
• Generation of new music
• Generation of various art forms
• Signal and image compression
• Creation of digital photographic enlargements
• Seismology
• Fractal in soil mechanics
• Computer and video game design, especially computer graphics for organic environments and as part of procedural generation
• Fractography and fracture mechanics
• Fractal antennas — Small size antennas using fractal shapes
• Small angle scattering theory of fractally rough systems
• T-shirts and other fashion
• Generation of patterns for camouflage, such as MARPAT
• Digital sundial
• Technical analysis of price series (see Elliott wave principle)

See also

References

Further reading

• Barnsley, Michael F., and Hawley Rising. Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0
• Falconer, Kenneth. Techniques in Fractal Geometry. John Willey and Sons, 1997. ISBN 0-471-92287-0
• Jürgens, Hartmut, Heins-Otto Peitgen, and Dietmar Saupe. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992. ISBN 0-387-97903-4
• Benoît B. Mandelbrot The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982. ISBN 0-7167-1186-9
• Peitgen, Heinz-Otto, and Dietmar Saupe, eds. The Science of Fractal Images. New York: Springer-Verlag, 1988. ISBN 0-387-96608-0
• Clifford A. Pickover, ed. Chaos and Fractals: A Computer Graphical Journey - A 10 Year Compilation of Advanced Research. Elsevier, 1998. ISBN 0-444-50002-2
• Jesse Jones, Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993. ISBN 1-878739-46-8.
• Hans Lauwerier, Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. ISBN 0-691-08551-X, cloth. ISBN 0-691-02445-6 paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5 and ISBN 978-0-19-850839-7. 
• Bernt Wahl, Peter Van Roy, Michael Larsen, and Eric Kampman Exploring Fractals on the Macintosh, Addison Wesley, 1995. ISBN 0-201-62630-6
• Nigel Lesmoir-Gordon. "The Colours of Infinity: The Beauty, The Power and the Sense of Fractals." ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set.
• Gouyet, Jean-François. Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996. ISBN 2-225-85130-1, and New York: Springer-Verlag, 1996. ISBN 0-387-94153-1. Out-of-print. Available in PDF version at [1].

External links

• Fractals at the Open Directory Project