Flavour (particle physics)

Flavour in particle physics
Flavour quantum numbers:
  • Baryon number: B
  • Lepton number: L
  • Strangeness: S
  • Charmness: C
  • Bottomness: B'
  • Topness: T
  • Isospin: I or Iz
  • Weak isospin: T or Tz
  • Electric charge: Q

Combinations:

  • Hypercharge: Y
    • Y = 2 (Q − Iz)
  • Weak hypercharge: YW
    • YW = 2 (Q − Tz)
    • X + 2YW = 5 (B − L)

Related topics:

  • CPT symmetry
  • CKM matrix
  • CP symmetry
  • Chirality

In particle physics, flavour or flavor (see spelling differences) is a quantum number of elementary particles related to their weak interactions. In the electroweak theory this symmetry is gauged, and flavour changing processes exist. In quantum chromodynamics, on the other hand, flavour is a global symmetry.

Contents

Definition

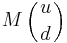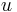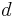If there are two or more particles which have identical interactions, then they may be interchanged without affecting the physics. Any (complex) linear combination of these two particles give the same physics, as long as they are orthogonal or perpendicular to each other. In other words, the theory possesses symmetry transformations such as M\left({u\atop d}\right), where u and d are the two fields, and 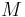M is any 2 x 2 unitary matrix with a unit determinant. Such matrices form a Lie group called SU(2) (see special unitary group). This is an example of flavour symmetry.

This symmetry is global for strong interactions, and gauged for weak interactions.

The term "flavour" was first coined for use in the quark model of hadrons in 1968. A name for the set of quantum numbers related to isospin, hypercharge and strangeness is said to have been found on the way to lunch by Murray Gell-Mann and Harald Fritzsch when they passed a Baskin-Robbins advertising 31 flavours.

Flavour quantum numbers

Leptons

All leptons carry a lepton number L  =  1. In addition, leptons carry weak isospin, Tz, which is −½ for the three charged leptons (i.e. e, μ and τ) and ½ for the three associated neutrinos. Each doublet of a charged lepton and a neutrino consisting of opposite Tz are said to constitute one generation of leptons. In addition, one defines a quantum number called weak hypercharge, YW which is −1 for the charged leptons and +1 for the neutrinos. Weak isospin and weak hypercharge are gauged in the Standard Model.

Leptons may be assigned the six flavour quantum numbers: electron number, muon number, tau number, and corresponding numbers for the neutrinos. These are conserved in electromagnetic interactions, but violated by weak interactions. Therefore, such flavour quantum numbers are not of great use. A quantum number for each generation is more useful. However, neutrinos of different generations can mix; that is, a neutrino of one flavour can transform into another flavour. The strength of such mixings is specified by a matrix called the MNS matrix.

Quarks

All quarks carry a baryon number B  =  ⅓. In addition they carry weak isospin, Tz  =  ±½. The positive Tz particles are called up-type quarks and the remainder are down-type quarks. Each doublet of up and down type quarks constitutes one generation of quarks.

Quarks have the following flavour quantum numbers:

These are useful quantum numbers since they are conserved by both the electromagnetic and strong forces. Out of them can be built the derived quantum numbers:

A quark of a given flavour is an eigenstate of the weak interaction part of the Hamiltonian: it will interact in a definite way with the W+, W− and Z bosons. On the other hand, a fermion of a fixed mass (an eigenstate of the kinetic and strong interaction parts of the Hamiltonian) is normally a superposition of various flavours. As a result, the flavour content of a quantum state may change as it propagates freely. The transformation from flavour to mass basis for quarks is given by the so-called Cabibbo-Kobayashi-Maskawa matrix (CKM matrix). By definition therefore, this matrix defines the strength of flavour changes under weak interactions of quarks.

The CKM matrix allows for CP violation if there are at least three generations.

Antiparticles and hadrons

Flavour quantum numbers are additive. Hence antiparticles have flavour equal in magnitude to the particle but opposite in sign. Hadrons inherit their flavour quantum number from their valence quarks: this is the basis of the classification in the quark model. The relations between the hypercharge, electric charge and other flavour quantum numbers hold for hadrons as well as quarks.

Quantum chromodynamics

(Flavour symmetry is closely related to chiral symmetry. This part of the article is best read along with the one on chirality (physics).)

Quantum chromodynamics contains six flavours of quarks. However, their masses differ. As a result, they are not strictly interchangeable with each other. Two of the flavours, called up and down, are close to having equal masses, and the theory of these two quarks possesses an approximate SU(2) symmetry. Under some circumstances one can take Nf flavours to have the same masses and obtain an effective SU(Nf) flavour symmetry.

Under some circumstances, the masses of the quarks can be neglected entirely. In that case, each flavour of quark possesses a chiral symmetry. One can then make flavour transformations independently on the left- and right-handed parts of each quark field. The flavour group is then a chiral group 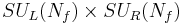SU_L(N_f)\times SU_R(N_f).

If all quarks have equal mass, then this chiral symmetry is broken to the vector symmetry of the diagonal flavour group which applies the same transformation to both helicities of the quarks. Such a reduction of the symmetry is called explicit symmetry breaking. The amount of explicit symmetry breaking is controlled by the current quark masses in QCD.

Even if quarks are massless, chiral flavour symmetry can be spontaneously broken if for some reason the vacuum of the theory contains a chiral condensate (as it does in low-energy QCD). This gives rise to an effective mass for the quarks, often identified with the valence quark mass in QCD.

Symmetries of QCD

Analysis of experiments indicate that the current quark masses of the lighter flavours of quarks are much smaller than the QCD scale, ΛQCD, hence chiral flavour symmetry is a good approximation to QCD for the up, down and strange quarks. The success of chiral perturbation theory and the even more naive chiral models spring from this fact. The valence quark masses extracted from the quark model are much larger than the current quark mass. This indicates that QCD has spontaneous chiral symmetry breaking with the formation of a chiral condensate. Other phases of QCD may break the chiral flavour symmetries in other ways.

Conservation laws

Absolutely conserved flavour quantum numbers are

All other flavour quantum numbers are violated by the electroweak interactions. Baryon number and lepton number are separately violated in the electroweak interactions through the chiral anomaly. Strong interactions conserve all flavours.

History

Some of the historical events that lead to the development of flavour symmetry are discussed in the article on isospin.

See also

References and external links