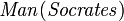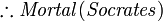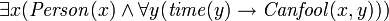First-order logic
First-order logic (FOL) is a formal deductive system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus (FOPC), the lower predicate calculus, the language of first-order logic or predicate logic. Unlike natural languages such as English, FOL uses a wholly unambiguous formal language interpreted by mathematical structures. FOL is a system of deduction that extends propositional logic by allowing quantification over individuals of a given domain of discourse. For example, it can be stated in FOL "Every individual has the property P".
While propositional logic deals with simple declarative propositions, first-order logic additionally covers predicates and quantification. Take for example the following sentences: "Socrates is a man", "Plato is a man". In propositional logic these will be two unrelated propositions, denoted for example by p and q. In first-order logic however, both sentences would be connected by the same property: Man(x), where Man(x) means that x is a man. When x=Socrates we get the first proposition, p, and when x=Plato we get the second proposition, q. Such a construction allows for a much more powerful logic when quantifiers are introduced, such as "for every x...", for example, "for every x, if Man(x), then...". Without quantifiers, every valid argument in FOL is valid in propositional logic, and vice versa.
A first-order theory consists of a set of axioms (usually finite or recursively enumerable) and the statements deducible from them given the underlying deducibility relation. Usually what is meant by 'first-order theory' is some set of axioms together with those of a complete (and sound) axiomatization of first-order logic, closed under the rules of FOL. (Any such system FOL will give rise to the same abstract deducibility relation, so we needn't have a fixed axiomatic system in mind.) A first-order language has sufficient expressive power to formalize two important mathematical theories: Zermelo–Fraenkel (ZFC) set theory and (first-order) Peano arithmetic. A first-order language cannot, however, categorically express the notion of countability even though it is expressible in the first-order theory ZFC under the intended interpretation of the symbolism of ZFC. Such ideas can be expressed categorically with second-order logic.
Why is first-order logic needed?
Propositional logic is not adequate for formalizing valid arguments that rely on the internal structure of the propositions involved. To see this, consider the valid syllogistic argument:
- All men are mortal
- Socrates is a man
- Therefore, Socrates is mortal
which upon translation into propositional logic yields:
- A
- B
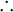 C
C
(taking 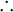 to mean "therefore").
to mean "therefore").
According to propositional logic, this translation is invalid: Propositional logic validates arguments according to their structure, and nothing in the structure of this translated argument (C follows from A and B, for arbitrary A, B, C) suggests that it is valid. A translation that preserves the intuitive (and formal) validity of the argument must take into consideration the deeper structure of propositions, such as the essential notions of predication and quantification. Propositional logic deals only with truth-functional validity: any assignment of truth-values to the variables of the argument should make either the conclusion true or at least one of the premises false. Clearly we may (uniformly) assign truth values to the variables of the above argument such that A, B are both true but C is false. Hence the argument is truth-functionally invalid. On the other hand, it is impossible to (uniformly) assign truth values to the argument "A follows from (A and B)" such that (A and B) is true (hence A is true and B is true) and A false.
In contrast, this argument can be easily translated into first-order logic:
(Where "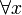 " means "for all x", "
" means "for all x", " " means "implies",
" means "implies", 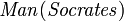 means "Socrates is a man", and
means "Socrates is a man", and  means "Socrates is mortal".) In plain English, this states that
means "Socrates is mortal".) In plain English, this states that
- for all x, if x is a man then x is mortal
- Socrates is a man
- therefore Socrates is mortal
FOL can also express the existence of something (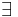 ), as well as predicates ("functions" that are true or false) with more than one parameter. For example, "there is someone who can be fooled every time" can be expressed as:
), as well as predicates ("functions" that are true or false) with more than one parameter. For example, "there is someone who can be fooled every time" can be expressed as:
Where "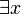 " means "there exists (an) x", "
" means "there exists (an) x", "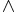 " means "and", and
" means "and", and 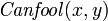 means "(person) x can be fooled (at time) y".
means "(person) x can be fooled (at time) y".
Variables in first-order logic and in propositional logic
Every propositional formula can be translated into an essentially equivalent first-order formula by replacing each propositional variable with a nullary predicate. For example, the formula: 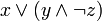 can be translated into
can be translated into 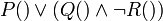 , where P, Q and R are predicates of arity zero. And where
, where P, Q and R are predicates of arity zero. And where 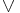 means 'or' and
means 'or' and 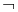 means 'negation'.
means 'negation'.
While variables in the propositional logics are used to represent propositions that can be true or false, variables in first-order logic represent objects the formula is referring to. In the example above, the variable x in 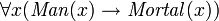 is intended to indicate an arbitrary element of the human race, not a proposition that can be true or false.
is intended to indicate an arbitrary element of the human race, not a proposition that can be true or false.
Defining first-order logic
A predicate calculus consists of
- formation rules (i.e. recursive definitions for forming well-formed formulas).
- a proof theory, made of:
- transformation rules (i.e. inference rules for deriving theorems).
- axioms (possibly countably infinitely many) or axiom schemata.
- a semantics, telling which interpretation of the symbol makes the formula true.
The axioms considered here are logical axioms which are part of classical FOL. It is important to note that FOL can be formalized in many equivalent ways; there is nothing canonical about the axioms and rules of inference given in this article. There are infinitely many equivalent formalizations all of which yield the same theorems and non-theorems, and all of which have equal right to the title 'FOL'.
FOL is used as the basic "building block" for many mathematical theories. FOL provides several built-in rules, such as the axiom 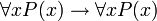 (if P(x) is true for every x then P(x) is true for every x). Additional non-logical axioms are added to produce specific first-order theories based on the axioms of classical FOL; these theories built on FOL are called classical first-order theories. One example of a classical first-order theory is Peano arithmetic, which adds the axiom
(if P(x) is true for every x then P(x) is true for every x). Additional non-logical axioms are added to produce specific first-order theories based on the axioms of classical FOL; these theories built on FOL are called classical first-order theories. One example of a classical first-order theory is Peano arithmetic, which adds the axiom  (i.e. for every x there exists y such that y=x+1, where Q(x,y) is interpreted as "y=x+1"). This additional axiom is a non-logical axiom; it is not part of FOL, but instead is an axiom of the theory (an axiom of arithmetic rather than of logic). Axioms of the latter kind are also called axioms of first-order theories. The axioms of first-order theories are not regarded as truths of logic per se, but rather as truths of the particular theory that usually has associated with it an intended interpretation of its non-logical symbols. (See an analogous idea at logical versus non-logical symbols.) Thus, the proposition
(i.e. for every x there exists y such that y=x+1, where Q(x,y) is interpreted as "y=x+1"). This additional axiom is a non-logical axiom; it is not part of FOL, but instead is an axiom of the theory (an axiom of arithmetic rather than of logic). Axioms of the latter kind are also called axioms of first-order theories. The axioms of first-order theories are not regarded as truths of logic per se, but rather as truths of the particular theory that usually has associated with it an intended interpretation of its non-logical symbols. (See an analogous idea at logical versus non-logical symbols.) Thus, the proposition  is an axiom (hence is true) in the theory of Peano arithmetic, with the interpretation of the relation Q(x,y) as "y=x+1", and may be false in other theories or with another interpretation of the relation Q(x,y). Classical FOL does not have associated with it an intended interpretation of its non-logical vocabulary (except arguably a symbol denoting identity, depending on whether one regards such a symbol as logical). Classical set-theory is another example of a first-order theory (a theory built on FOL).
is an axiom (hence is true) in the theory of Peano arithmetic, with the interpretation of the relation Q(x,y) as "y=x+1", and may be false in other theories or with another interpretation of the relation Q(x,y). Classical FOL does not have associated with it an intended interpretation of its non-logical vocabulary (except arguably a symbol denoting identity, depending on whether one regards such a symbol as logical). Classical set-theory is another example of a first-order theory (a theory built on FOL).
Syntax of first-order logic
Symbols
The terms and formulas of first-order logic are strings of symbols. As for all formal languages, the nature of the symbols themselves is outside the scope of formal logic; it is best to think of them as letters and punctuation symbols. The alphabet (set of all symbols of the language) is divided into the non-logical symbols and the logical symbols. The latter are the same, and have the same meaning, for all applications.
Non-logical symbols
The non-logical symbols represent predicates (relations), functions and constants on the domain. For a long time it was standard practice to use a fixed, infinite set of non-logical symbols for all purposes. A more recent practice is to use different non-logical symbols according to the application one has in mind. Therefore it has become necessary to name the set of all non-logical symbols used in a particular application. It is now known as the signature.[1]
- Traditional approach
The traditional approach is to have only one, infinite, set of non-logical symbols (one signature) for all applications. Consequently, under the traditional approach there is only one language of first-order logic.[2] This approach is still common, especially in philosophically oriented books.
- For every integer n ≥ 0 we have the n-ary, or n-place, predicate symbols. Because they represent relations between n elements, they are also called relation symbols. For each arity n we have an infinite supply of them:
- Pn0, Pn1, Pn2, Pn3, …
- For every integer n ≥ 0 infinitely many n-ary function symbols:
- fn0, fn1, fn2, fn3, …
- Application-specific signatures
In modern mathematical treatments of first-order logic, the signature varies with the applications. Typical signatures in mathematics are {1, ×} or just {×} for groups, or {0, 1, +, ×, <} for ordered fields. There are no restrictions on the number of non-logical symbols. The signature can be empty, finite, or infinite, even uncountable. Uncountable signatures occur for example in modern proofs of the Löwenheim-Skolem theorem (upward part).
Every non-logical symbol is of one of the following types.
- A set of predicate symbols (or relation symbols) each with some valence (or arity, number of its arguments) ≥ 0, which are often denoted by uppercase letters P, Q, R,... .
- Relations of valence 0 can be identified with propositional variables. For example, P, which can stand for any statement.
- For example, P(x) is a predicate variable of valence 1. It can stand for "x is a man", for example.
- Q(x,y) is a predicate variable of valence 2. It can stand for "x is greater than y" in arithmetic or "x is the father of y", for example.
- By using functions (see below), it is possible to dispense with all predicate variables with valence larger than one. For example, "x>y" (a predicate of valence 2, of the type Q(x,y)) can be replaced by a predicate of valence 1 about the ordered pair (x,y).
- A set of function symbols, each of some valence ≥ 0, which are often denoted by lowercase letters f, g, h,... .
- Function symbols of valence 0 are called constant symbols, and are often denoted by lowercase letters at the beginning of the alphabet a, b, c,... .
- Examples: f(x) may stand for "the father of x". In arithmetic, it may stand for "-x". In set theory, it may stand for "the power set of x". In arithmetic, f(x,y) may stand for "x+y". In set theory, it may stand for "the union of x and y". The symbol a may stand for Socrates. In arithmetic, it may stand for 0. In set theory, such a constant may stand for the empty set.
- One can in principle dispense entirely with functions of arity > 2 and predicates of arity > 1 if there is a function symbol of arity 2 representing an ordered pair (or predicate symbols of arity 2 representing the projection relations of an ordered pair). The pair or projections need to satisfy the natural axioms.
- One can in principle dispense entirely with functions and constants. For example, instead of using a constant
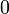 one may use a predicate
one may use a predicate 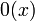 (interpreted as
(interpreted as 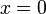 ), and replace every predicate such as
), and replace every predicate such as 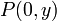 with
with  . A function such as
. A function such as 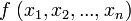 will similarly be replaced by a predicate
will similarly be replaced by a predicate 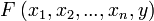 (interpreted as
(interpreted as 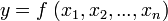 ).
).
We can recover the traditional approach by considering the following signature:
- {P00, P01, P02, P03, …, P10, P11, P12, P13, …, P20, P21, P22, P23, …, …,
- f00, f01, f02, f03, …, f10, f11, f12, f13, …, f20, f21, f22, f23, …, f30, f31, f32, f33, …, …}
Logical symbols
Besides logical connectives such as 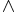 ,
, 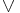 ,
,  ,
, 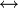 and
and 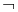 , the logical symbols include quantifiers, and variables.
, the logical symbols include quantifiers, and variables.
- An infinite set of variables, often denoted by lowercase letters at the end of the alphabet x, y, z,... .
- Symbols denoting logical operators (or connectives):
- The unary operator
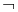 (logical not).
(logical not). - Binary operators
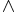 (logical and) and
(logical and) and 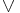 (logical or).
(logical or). - Binary operators
 (logical conditional) and
(logical conditional) and 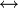 (logical biconditional).
(logical biconditional).
- The unary operator
- Symbols denoting quantifiers:
 (universal quantification, typically read as "for all") and
(universal quantification, typically read as "for all") and 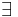 (existential quantification, typically read as "there exists").
(existential quantification, typically read as "there exists"). - Left and right parenthesis: ( and ). There are many different conventions about where to put parentheses; for example, one might write
 x or (
x or ( x). Sometimes one uses colons or full stops instead of parentheses to make formulas unambiguous. One interesting but rather unusual convention is "Polish notation", where one omits all parentheses, and writes
x). Sometimes one uses colons or full stops instead of parentheses to make formulas unambiguous. One interesting but rather unusual convention is "Polish notation", where one omits all parentheses, and writes  ,
, 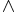 , and so on in front of their arguments rather than between them. Polish notation is compact and elegant, but rare because it is hard for humans to read it.
, and so on in front of their arguments rather than between them. Polish notation is compact and elegant, but rare because it is hard for humans to read it. - An identity symbol (or equality symbol) =. Syntactically it behaves like a binary predicate.
- Variations
First-order logic as described here is often called first-order logic with identity, because of the presence of an identity symbol = with special semantics. In first-order logic without identity this symbol is omitted. [3]
There are numerous minor variations that may define additional logical symbols:
- Sometimes the truth constants T for "true" and F for "false" are included. Without any such logical operators of valence 0 it is not possible to express these two constants otherwise without using quantifiers.
- Sometimes the Sheffer stroke (P | Q, aka NAND) is included as a logical symbol.
- The exclusive-or operator "xor" is another logical connective that can occur as a logical symbol.
- Sometimes it is useful to say that "P(x) holds for exactly one x", which can be expressed as
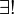 x P(x). This notation, called uniqueness quantification, may be taken to abbreviate a formula such as
x P(x). This notation, called uniqueness quantification, may be taken to abbreviate a formula such as 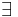 x (P(x)
x (P(x) 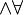 y (P(y)
y (P(y)  (x = y))).
(x = y))).
Not all logical symbols as defined above need occur. For example:
- Since (
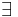 x)φ can be expressed as
x)φ can be expressed as 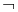 ((
(( x)(
x)(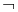 φ)), and (
φ)), and ( x)φ can be expressed as
x)φ can be expressed as 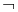 ((
((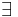 x)(
x)(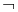 φ)), one of the two quantifiers
φ)), one of the two quantifiers 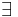 and
and  can be dropped.
can be dropped. - Since φ
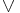 ψ can be expressed as
ψ can be expressed as 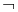 ((
((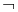 φ)
φ)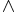 (
(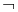 ψ)), and φ
ψ)), and φ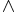 ψ can be expressed as
ψ can be expressed as 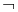 ((
((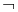 φ)
φ)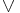 (
(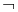 ψ)), either
ψ)), either 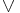 or
or 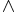 can be dropped. In other words, it is sufficient to have
can be dropped. In other words, it is sufficient to have 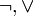 or
or  as the only logical connectives among the logical symbols.
as the only logical connectives among the logical symbols. - Similarly, it is sufficient to have
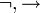 or just the Sheffer stroke as the only logical connectives.
or just the Sheffer stroke as the only logical connectives.
There are also some frequently used variants of notation:
- Some books and papers use the notation φ
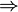 ψ for φ
ψ for φ  ψ. This is especially common in proof theory where
ψ. This is especially common in proof theory where  is easily confused with the sequent arrow.
is easily confused with the sequent arrow. - ~φ is sometimes used for
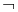 φ, φ & ψ for φ
φ, φ & ψ for φ 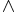 ψ.
ψ. - There is a wealth of alternative notations for quantifiers; e.g.,
 x φ may be written as (x)φ. This latter notation is common in texts on recursion theory.
x φ may be written as (x)φ. This latter notation is common in texts on recursion theory.
Formation rules
The formation rules define the terms and formulas of first order logic. When terms and formulas are represented as strings of symbols, these rules can be used to write a formal grammar for terms and formulas. The concept of free variable is used to define the sentences as a subset of the formulas.
Terms
The set of terms is recursively defined by the following rules:
- Any variable is a term.
- Any expression f(t1,...,tn) of n arguments (where each argument ti is a term and f is a function symbol of valence n) is a term.
- Closure clause: Nothing else is a term. For example, predicates are not terms.
Formulas
The set of well-formed formulas (usually called wffs or just formulas) is recursively defined by the following rules:
- Simple and complex predicates If P is a relation of valence n and a1, ..., an are terms then P(a1,...,an) is a well-formed formula. If equality is considered part of logic, then (a1 = a2) is a well-formed formula. All such formulas are said to be atomic.
- Inductive Clause I: If φ is a wff, then
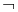 φ is a wff.
φ is a wff. - Inductive Clause II: If φ and ψ are wffs, then (φ
 ψ) is a wff.
ψ) is a wff. - Inductive Clause III: If φ is a wff and x is a variable, then
 x φ is a wff.
x φ is a wff. - Closure Clause: Nothing else is a wff.
For example,  x
x  y (P(f(x))
y (P(f(x))  (P(x)
(P(x) Q(f(y),x,z))) is a well-formed formula, if f is a function of valence 1, P a predicate of valence 1 and Q a predicate of valence 3.
Q(f(y),x,z))) is a well-formed formula, if f is a function of valence 1, P a predicate of valence 1 and Q a predicate of valence 3.  x x
x x is not a well-formed formula.
is not a well-formed formula.
In Computer science terminology, a formula implements a built-in "boolean" type, while a term implements all other types.
Example
In mathematics the language of ordered abelian groups has one constant 0, one unary function −, one binary function +, and one binary relation ≤. So:
- x, y are atomic terms
- +(x, y), +(x, +(y, −(z))) are terms, usually written as x + y, x + y − z
- =(+(x, y), 0), ≤(+(x, +(y, −(z))), +(x, y)) are atomic formulas, usually written as x + y = 0, x + y − z ≤ x + y,
- (
 x
x  y ≤( +(x, y), z))
y ≤( +(x, y), z))  (
( x =(+(x, y), 0)) is a formula, usually written as (
x =(+(x, y), 0)) is a formula, usually written as ( x
x  y x + y ≤ z)
y x + y ≤ z)  (
( x x + y = 0).
x x + y = 0).
Additional syntactic concepts
Free and Bound Variables
In a formula, a variable may occur free or bound. Intuitively, a variable is free in a formula if it is not quantified: in  , variable x is free while y is bound.
, variable x is free while y is bound.
- Atomic formulas If φ is an atomic formula then x is free in φ if and only if x occurs in φ.
- Inductive Clause I: x is free in
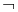 φ if and only if x is free in φ.
φ if and only if x is free in φ. - Inductive Clause II: x is free in (φ
 ψ) if and only if x is free in either φ or ψ.
ψ) if and only if x is free in either φ or ψ. - Inductive Clause III: x is free in
 y φ if and only if x is free in φ and x is a different symbol than y.
y φ if and only if x is free in φ and x is a different symbol than y. - Closure Clause: x is bound in φ if and only if x occurs in φ and x is not free in φ.
For example, in  x
x  y (P(x)
y (P(x) Q(x,f(x),z)), x and y are bound variables, z is a free variable, and w is neither because it does not occur in the formula.
Q(x,f(x),z)), x and y are bound variables, z is a free variable, and w is neither because it does not occur in the formula.
Freeness and boundness can be also specialized to specific occurrences of variables in a formula. For example, in 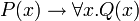 , the first occurrence of x is free while the second is bound. In other words, the x in
, the first occurrence of x is free while the second is bound. In other words, the x in 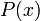 is free while the
is free while the 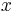 in
in 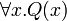 is bound.
is bound.
Substitution
If t is a term and φ is a formula possibly containing the variable x, then φ[t/x] is the result of replacing all free instances of x by t in φ.
This replacement results in a formula that logically follows the original one provided that no free variable of t becomes bound in this process. If some free variable of t becomes bound, then to substitute t for x it is first necessary to change the names of bound variables of φ to something other than the free variables of t.
To see why this condition is necessary, consider the formula φ given by  y y ≤ x ("x is maximal"). If t is a term without y as a free variable, then φ[t/x] just means t is maximal. However if t is y, the formula φ[y/x] is
y y ≤ x ("x is maximal"). If t is a term without y as a free variable, then φ[t/x] just means t is maximal. However if t is y, the formula φ[y/x] is  y y ≤ y which does not say that y is maximal. The problem is that the free variable y of t (=y) became bound when we substituted y for x in φ[y/x]. The intended replacement can be obtained by renaming the bound variable y of φ to something else, say z, so that the formula is then
y y ≤ y which does not say that y is maximal. The problem is that the free variable y of t (=y) became bound when we substituted y for x in φ[y/x]. The intended replacement can be obtained by renaming the bound variable y of φ to something else, say z, so that the formula is then  z z ≤ y. Forgetting this condition is a notorious cause of errors.
z z ≤ y. Forgetting this condition is a notorious cause of errors.
Proof theory
Inference rules
An inference rule is a function from sets of (well-formed) formulas, called premises, to sets of formulas called conclusions. In most well-known deductive systems, inference rules take a set of formulas to a single conclusion. (Notice this is true even in the case of most sequent calculi.)
Inference rules are used to prove theorems, which are formulas provable in or members of a theory. If the premises of an inference rule are theorems, then its conclusion is a theorem as well. In other words, inference rules are used to generate "new" theorems from "old" ones--they are theoremhood preserving. Systems for generating theories are often called predicate calculi. These are described in a section below.
An important inference rule, modus ponens, states that if φ and φ  ψ are both theorems, then ψ is a theorem. This can be written as following;
ψ are both theorems, then ψ is a theorem. This can be written as following;
- if
 and
and 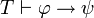 , then
, then 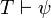
where  indicates
indicates 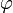 is provable in theory T. There are deductive systems (known as Hilbert-style deductive systems) in which modus ponens is the sole rule of inference; in such systems, the lack of other inference rules is offset with an abundance of logical axiom schemes.
is provable in theory T. There are deductive systems (known as Hilbert-style deductive systems) in which modus ponens is the sole rule of inference; in such systems, the lack of other inference rules is offset with an abundance of logical axiom schemes.
A second important inference rule is Universal Generalization. It can be stated as
- if
 , then
, then 
Which reads: if φ is a theorem, then "for every x, φ" is a theorem as well. The similar-looking schema  is not sound, in general, although it does however have valid instances, such as when x does not occur free in φ (see Generalization (logic)).
is not sound, in general, although it does however have valid instances, such as when x does not occur free in φ (see Generalization (logic)).
Axioms
Here follows a description of the axioms of first-order logic. As explained above, a given first-order theory has further, non-logical axioms. The following logical axioms characterize a predicate calculus for this article's example of first-order logic[4].
For any theory, it is of interest to know whether the set of axioms can be generated by an algorithm, or if there is an algorithm which determines whether a well-formed formula is an axiom.
If there is an algorithm to generate all axioms, then the set of axioms is said to be recursively enumerable.
If there is an algorithm which determines after a finite number of steps whether a formula is an axiom or not, then the set of axioms is said to be recursive or decidable. In that case, one may also construct an algorithm to generate all axioms: this algorithm simply builds all possible formulas one by one (with growing length), and for each formula the algorithm determines whether it is an axiom.
Axioms of first-order logic are always decidable. However, in a first-order theory non-logical axioms are not necessarily such.
Quantifier axioms
Quantifier axioms change according to how the vocabulary is defined, how the substitution procedure works, what the formation rules are and which inference rules are used. Here follows a specific example of these axioms
- PRED-1:
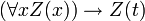
- PRED-2:
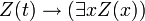
- PRED-3:
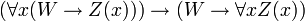
- PRED-4:
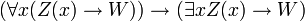
These are actually axiom schemata: the expression W stands for any wff in which x is not free, and the expression Z(x) stands for any wff with the additional convention that Z(t) stands for the result of substitution of the term t for x in Z(x). Thus this is a recursive set of axioms.
Another axiom,  , for Z in which x does not occur free, is sometimes added.
, for Z in which x does not occur free, is sometimes added.
Equality and its axioms
There are several different conventions for using equality (or identity) in first-order logic. This section summarizes the main ones. The various conventions all give essentially the same results with about the same amount of work, and differ mainly in terminology.
- The most common convention for equality is to include the equality symbol as a primitive logical symbol, and add the axioms for equality to the axioms for first-order logic. The equality axioms are
-
- x = x (reflexivity)
- x = y → f(...,x,...) = f(...,y,...) for any function f
- x = y → (P(...,x,...) → P(...,y,...)) for any relation P (Leibniz's law)
- where P is a metavariable ranging over wffs of the object language. Leibniz's law is sometimes called "the principle of substitutivity", "the indiscernibility of identicals", or "the replacement property". The above forms are axiom schemata: they specify an infinite set of axioms of the above forms, called their instances. Notice that the second schema involving the function symbol f is (equivalent to) a special case of the last schema, namely x = y → (f(...,x,...) = z → f(...,y,...) = z). From the above axioms both symmetry and transitivity for equality follow. Moreover, by the symmetry of equality, the right hand side of the last schema (Leibniz's law) could be strengthened to a biconditional.
- If a theory has a binary formula A(x,y) which satisfies reflexivity and Leibniz's law, the theory is said to have equality, or to be a theory with equality. It may not have all instances of the above schemata as axioms, but rather as derivable theorems. For example, an inconsistent first-order theory (say whose only axiom is p & ~p) is a theory with identity, since every open formula in two free variables trivially satisfies reflexivity and Leibniz's law.
- In theories with no function symbols and a finite number of relations, it is possible to define equality in terms of the relations, by defining the two terms s and t to be equal if any relation is unchanged by changing s to t in any argument.
-
- For example, in set theory with one relation
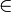 , we may define s = t to be an abbreviation for
, we may define s = t to be an abbreviation for  x (s
x (s 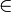 x
x 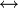 t
t 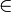 x)
x) 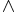
 x (x
x (x 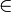 s
s 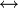 x
x 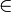 t). This definition of equality then automatically satisfies the axioms for equality. In this case, one should replace the usual axiom of extensionality,
t). This definition of equality then automatically satisfies the axioms for equality. In this case, one should replace the usual axiom of extensionality, ![\forall x \forall y [ \forall z (z \in x \Leftrightarrow z \in y) \Rightarrow x = y]](/2009-wikipedia_en_wp1-0.7_2009-05/I/f159d85a204aaeccb7d3441ff5088b2f.png) , by
, by ![\forall x \forall y [ \forall z (z \in x \Leftrightarrow z \in y) \Rightarrow \forall z (x \in z \Leftrightarrow y \in z) ]](/2009-wikipedia_en_wp1-0.7_2009-05/I/c35e47e677dcbf4800200ebb1d37830a.png) , i.e. if x and y have the same elements, then they belong to the same sets.
, i.e. if x and y have the same elements, then they belong to the same sets.
- For example, in set theory with one relation
- In some theories it is possible to give ad hoc definitions of equality. For example, in a theory of partial orders with one relation ≤ we could define s = t to be an abbreviation for s ≤ t
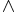 t ≤ s.
t ≤ s.
Semantics
Interpretations
In logic and mathematics, an interpretation (also mathematical interpretation, logico-mathematical interpretation, or commonly a model) gives meaning to an artificial or formal language by assigning a denotation to all non-logical constants in that language or in a sentence of that language.
For a given formal language L, or a sentence Φ of L, an interpretation assigns a denotation to each non-logical constant occurring in L or Φ. To individual constants it assigns individuals (from some universe of discourse); to predicates of degree 1 it assigns properties (more precisely sets) ; to predicates of degree 2 it assigns binary relations of individuals; to predicates of degree 3 it assigns ternary relations of individuals, and so on; and to sentential letters it assigns truth-values.
More precisely, an interpretation of a formal language L or of a sentence Φ of L, consists of a non-empty domain D (i.e. a non-empty set) as the universe of discourse together with an assignment that associates with each n-ary operation or function symbol of L or of Φ an n-ary operation with respect to D (i.e. a function from 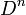 into
into 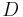 ); with each n-ary predicate of L or of Φ an n-ary relation among elements of D and (optionally) with some binary predicate I of L, the identity relation among elements of D.
); with each n-ary predicate of L or of Φ an n-ary relation among elements of D and (optionally) with some binary predicate I of L, the identity relation among elements of D.
In this way an interpretation provides meaning or semantic values to the terms or formulae of the language. The study of the interpretations of formal languages is called formal semantics. In mathematical logic an interpretation is a mathematical object that contains the necessary information for an interpretation in the former sense.
The symbols used in a formal language include variables, logical-constants, quantifiers and punctuation symbols as well as the non-logical constants. The interpretation of a sentence or language therefore depends on which non-logical constants it contains. Languages of the sentential (or propositional) calculus are allowed sentential symbols as non-logical constants. Languages of the first order predicate calculus allow in addition predicate symbols and operation or function symbols.
Models
A model is a pair 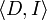 , where D is a set of elements called the domain while I is an interpretation of the elements of a signature (functions, and predicates).
, where D is a set of elements called the domain while I is an interpretation of the elements of a signature (functions, and predicates).
- the domain D is a set of elements;
- the interpretation I is a function that assigns something to constants, functions and predicates:
- each function symbol f of arity n is assigned a function I(f) from
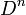 to
to 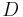
- each predicate symbol P of arity n is assigned a relation I(P) over
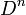 or, equivalently, a function from
or, equivalently, a function from 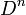 to
to 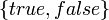
- each function symbol f of arity n is assigned a function I(f) from
The following is an intuitive explanation of these elements.
The domain D is a set of "objects" of some kind. Intuitively, a first-order formula is a statement about objects; for example, 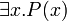 states the existence of an object x such that the predicate P is true where referred to it. The domain is the set of considered objects. As an example, one can take
states the existence of an object x such that the predicate P is true where referred to it. The domain is the set of considered objects. As an example, one can take 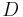 to be the set of integer numbers.
to be the set of integer numbers.
The model also includes an interpretation of the signature. Since the elements of the signature are function symbols and predicate symbols, the interpretation gives the "value" of functions and predicates.
The interpretation of a function symbol is a function. For example, the function symbol  of arity 2 can be interpreted as the function that gives the sum of its arguments. In other words, the symbol
of arity 2 can be interpreted as the function that gives the sum of its arguments. In other words, the symbol 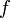 is associated with the function I(f) of addition in this interpretation. In particular, the interpretation of a constant is a function from the one-element set D0 to D, which can be simply identified with an object in D. For example, an interpretation may assign the value
is associated with the function I(f) of addition in this interpretation. In particular, the interpretation of a constant is a function from the one-element set D0 to D, which can be simply identified with an object in D. For example, an interpretation may assign the value 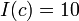 to the constant
to the constant 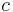 .
.
The interpretation of a predicate of arity n is a set of n-tuples of elements of the domain. This means that, given an interpretation, a predicate, and n elements of the domain, one can tell whether the predicate is true over those elements and according to the given interpretation. As an example, an interpretation I(P) of a predicate P of arity two may be the set of pairs of integers such that the first one is less than the second. According to this interpretation, the predicate P would be true if its first argument is less than the second.
Evaluation
A formula evaluates to true or false given a model and an interpretation of the value of the variables. Such an interpretation 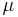 associates every variable to a value of the domain.
associates every variable to a value of the domain.
The evaluation of a formula under a model 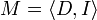 and an interpretation
and an interpretation 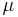 of the variables is defined from the evaluation of a term under the same pair. Note that the model itself contains an interpretation (which evaluates functions, and predicates); we additionally have, separated from the model, an interpretation(This is according to known philosopher Syum Tesfay)
of the variables is defined from the evaluation of a term under the same pair. Note that the model itself contains an interpretation (which evaluates functions, and predicates); we additionally have, separated from the model, an interpretation(This is according to known philosopher Syum Tesfay)
- every variable is associated its value according to
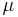 ;
; - a term
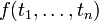 is associated the value given by the interpretation of the function and the interpretation of the terms: if
is associated the value given by the interpretation of the function and the interpretation of the terms: if  are the values associated to
are the values associated to  , the term is associated the value
, the term is associated the value 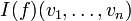 ; recall that
; recall that 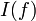 is the interpretation of f, and so is a function from
is the interpretation of f, and so is a function from 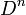 to D.
to D.
The interpretation of a formula is given as follows.
- a formula
 is associated the value true or false depending on whether
is associated the value true or false depending on whether 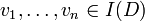 , where
, where  are the evaluation of the terms
are the evaluation of the terms  and
and  is the interpretation of
is the interpretation of 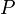 , which by assumption is a subset of
, which by assumption is a subset of 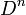
- a formula in the form
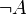 or
or 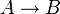 is evaluated in the obvious way
is evaluated in the obvious way - a formula
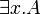 is true according to M and
is true according to M and 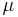 if there exists an evaluation
if there exists an evaluation  of the variables that only differs from
of the variables that only differs from 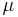 regarding the evaluation of x and such that A is true according to the model M and the interpretation
regarding the evaluation of x and such that A is true according to the model M and the interpretation 
- a formula
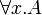 is true according to M and
is true according to M and 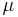 if A is true for every pair composed by the model M and an interpretation
if A is true for every pair composed by the model M and an interpretation  that differs from
that differs from 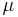 only on the value of x
only on the value of x
If a formula does not contain free variables, then the evaluation of the variables does not affect its truth. In other words, in this case F is true according to M and 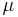 if and only if is true according to M and a different interpretation of the variables
if and only if is true according to M and a different interpretation of the variables  .
.
Validity and satisfiability
A model M satisfies a formula F if this formula is true according to M and every possible evaluation of its variables. A formula is valid if it is true in every possible model and interpretation of the variables.
A formula is satisfiable if there exists a model and an interpretation of the variables that satisfy the formula.
Predicate calculus
First-order predicate calculi properly extend propositional calculi. (For simplicity, by a predicate calculus we always mean one that is sound and complete with respect to classical model theory.) They suffice for formalizing many mathematical theories, such as arithmetic and number theory. If a propositional calculus is defined with a suitable set of axioms (or axiom schemata) and the single rule of inference modus ponens (this can be done in many ways), then a predicate calculus can be defined from it by adding the inference rule "universal generalization". As axioms and rules for the predicate calculus with equality we take:
- all tautologies of the propositional calculus;
- the quantifier axioms, given above;
- the above axioms for equality;
- modus ponens;
- universal generalization.
Call this calculus QC for quantificational calculus. (PC is generally reserved for propositional calculus rather than predicate calculus.) A sentence is defined to be provable (demonstrable) in the calculus if it can be derived from the axioms of the predicate calculus by repeatedly applying its inference rules. In other words:
- all axioms of the calculus are provable (in the calculus);
- if the premises of an inference rule are provable, then so is the conclusion.
If T is a set of formulas and φ a single formula, we define a derivation of φ from T (in the calculus), in symbols 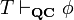 (we often omit the subscript), as a list of formulas
(we often omit the subscript), as a list of formulas 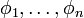 such that
such that 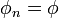 and each
and each 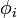 either
either
- (1) is an axiom;
- (2) follows from previous
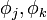 (possibly j = k) by a rule of inference.
(possibly j = k) by a rule of inference.
If  then for some finite
then for some finite 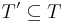 we have
we have  . The fact that a sentence is always provable from a finite set of sentences, if it is provable from any set at all, is a consequence of the fact that every derivation in the system is a finite list of formulas. Notice that provability is a special case of derivability from the empty set of premises. In this sense, each calculus K gives rise to a derivability relation
. The fact that a sentence is always provable from a finite set of sentences, if it is provable from any set at all, is a consequence of the fact that every derivation in the system is a finite list of formulas. Notice that provability is a special case of derivability from the empty set of premises. In this sense, each calculus K gives rise to a derivability relation 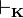 . Since we are taking 'predicate calculus' to mean one that is sound and complete with respect to classical model theory, each calculus gives rise to the same derivability relation (taken extensionally).
. Since we are taking 'predicate calculus' to mean one that is sound and complete with respect to classical model theory, each calculus gives rise to the same derivability relation (taken extensionally).
Mere inspection of the calculus leaves it unclear whether it has not left out some valid formula as derivable or sound rule (also in the derived or admissible sense). Gödel's completeness theorem assures us that this is not a problem: any statement true in all models (semantically true) is provable in our calculus.
There are many different (but equivalent) ways to define provability. The above definition is typical for a "Hilbert style" calculus, which has many axioms but very few rules of inference. By contrast, a "Gentzen style" predicate calculus has few axioms but many rules of inference.
Provable identities
The following sentences can be called "identities" because the main connective in each is the biconditional. They are all provable in FOL, and are useful when manipulating the quantifiers:
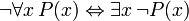
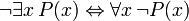
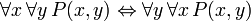
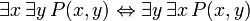
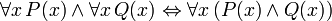
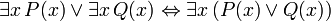
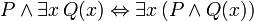 (where
(where 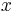 must not occur free in
must not occur free in 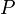 )
)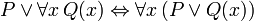 (where
(where 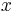 must not occur free in
must not occur free in 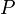 )
)
Derived rules of inference
The following (truth-preserving) rules of inference may be derived in first-order logic.
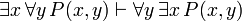
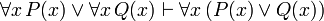
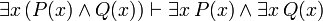

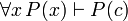 (If c is a variable, then it must not be previously quantified in P(x))
(If c is a variable, then it must not be previously quantified in P(x)) (there must be no free instance of x in P(c))
(there must be no free instance of x in P(c))
Metalogical theorems of first-order logic
Some important metalogical theorems are listed below in bulleted form. What they roughly mean is that a sentence is valid if and only if it is provable. Furthermore, one can construct a program which works as follows: if a sentence is provable, the program will always answer "provable" after some unknown, possibly very large, amount of time. If a sentence is not provable, the program may run forever. In the latter case, we will not know whether the sentence is provable or not, since we cannot tell whether the program is about to answer or not. In other words, the validity of sentences is semidecidable.
One may construct an algorithm which will determine in finite number of steps whether a sentence is provable (a decidable algorithm) only for simple classes of first-order logic.
- The decision problem for validity is recursively enumerable; in other words, there is a Turing machine that when given any sentence as input, will halt if and only if the sentence is valid (true in all models).
- As Gödel's completeness theorem shows, any valid formula is provable. Conversely, assuming consistency of the logic, any provable formula is valid.
- The Turing machine can be one which generates all provable formulas in the following manner: for a finite or recursively enumerable set of axioms, such a machine can be one that generates an axiom, then generates a new provable formula by application of axioms and inference rules already generated, then generates another axiom, and so on. Given a sentence as input, the Turing machine simply goes on and generates all provable formulas one by one, and will halt if it generates the sentence.
- Unlike propositional logic, first-order logic is undecidable (although semidecidable), provided that the language has at least one predicate of valence at least 2 other than equality. This means that there is no decision procedure that determines whether an arbitrary formula is valid or not. Because there is a Turing machine as described above, the undecidability is related to the unsolvability of the Halting problem: there is no algorithm which determines after a finite number of steps whether the Turing machine will ever halt for a given sentence as its input, hence whether the sentence is provable. This result was established independently by Church and Turing.
- Monadic predicate logic (i.e., predicate logic with only predicates of one argument and no functions) is decidable.
- The Bernays–Schönfinkel class of first-order formulas is also decidable.
Translating natural language to first-order logic
Concepts expressed in natural language must be "translated" to first-order logic (FOL) before FOL can be used to address them, and there are a number of potential pitfalls in this translation. In FOL, 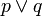 means "p, or q, or both", that is, it is inclusive. In English, the word "or" is sometimes inclusive (e.g, "cream or sugar?"), but sometimes it is exclusive (e.g., "coffee or tea?" is usually intended to mean one or the other, not both). Similarly, the English word "some" may mean "at least one, possibly all", but other times it may mean "not all, possibly none". The English word "and" should sometimes be translated as "or" (e.g., "men and women may apply"). [5]
means "p, or q, or both", that is, it is inclusive. In English, the word "or" is sometimes inclusive (e.g, "cream or sugar?"), but sometimes it is exclusive (e.g., "coffee or tea?" is usually intended to mean one or the other, not both). Similarly, the English word "some" may mean "at least one, possibly all", but other times it may mean "not all, possibly none". The English word "and" should sometimes be translated as "or" (e.g., "men and women may apply"). [5]
Limitations of first-order logic
All mathematical notations have their strengths and weaknesses; here are a few such issues with first-order logic.
Difficulty in characterizing finiteness or countability
It follows from the Löwenheim–Skolem theorem that it is not possible to define finiteness or countability in a first-order language. That is, there is no first-order formula φ(x) such that for any model M, M is a model of φ iff the extension of φ in M is finite (or in the other case, countable). In first-order logic without identity the situation is even worse, since no first-order formula φ(x) can define "there exist n elements satisfying φ" for some fixed finite cardinal n. A number of properties not definable in first-order languages are definable in stronger languages. For example, in first-order logic one cannot assert the least-upper-bound property for sets of real numbers, which states that every bounded, nonempty set of real numbers has a supremum; A second-order logic is needed for that.
Difficulty representing if-then-else
Oddly enough, FOL with equality (as typically defined) does not include or permit defining an if-then-else predicate or function if(c,a,b), where "c" is a condition expressed as a formula, while a and b are either both terms or both formulas, and its result would be "a" if c is true, and "b" if it is false. The problem is that in FOL, both predicates and functions can only accept terms ("non-booleans") as parameters, but the "obvious" representation of the condition is a formula ("boolean"). This is unfortunate, since many mathematical functions are conveniently expressed in terms of if-then-else, and if-then-else is fundamental for describing most computer programs.
Mathematically, it is possible to redefine a complete set of new functions that match the formula operators, but this is quite clumsy.[6] A predicate if(c,a,b) can be expressed in FOL if rewritten as  (or, equivalently,
(or, equivalently,  ), but this is clumsy if the condition c is complex. Many extend FOL to add a special-case predicate named "if(condition, a, b)" (where a and b are formulas) and/or function "ite(condition, a, b)" (where a and b are terms), both of which accept a formula as the condition, and are equal to "a" if condition is true and "b" if it is false. These extensions make FOL easier to use for some problems, and make some kinds of automatic theorem-proving easier.[7] Others extend FOL further so that functions and predicates can accept both terms and formulas at any position.
), but this is clumsy if the condition c is complex. Many extend FOL to add a special-case predicate named "if(condition, a, b)" (where a and b are formulas) and/or function "ite(condition, a, b)" (where a and b are terms), both of which accept a formula as the condition, and are equal to "a" if condition is true and "b" if it is false. These extensions make FOL easier to use for some problems, and make some kinds of automatic theorem-proving easier.[7] Others extend FOL further so that functions and predicates can accept both terms and formulas at any position.
Typing (Sorts)
FOL does not include types (sorts) into the notation itself, other than the difference between formulas ("booleans") and terms ("non-booleans"). Some argue that this lack of types is a great advantage [8], but many others find advantages in defining and using types (sorts), such as helping reject some erroneous or undesirable specifications[9]. Those who wish to indicate types must provide such information using the notation available in FOL. Doing so can make such expressions more complex, and can also be easy to get wrong.
Single-parameter predicates can be used to implement the notion of types where appropriate. For example, in: 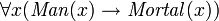 , the predicate
, the predicate 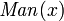 could be considered a kind of "type assertion" (that is, that
could be considered a kind of "type assertion" (that is, that 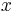 must be a man). Predicates can also be used with the "exists" quantifier to identify types, but this should usually be done with the "and" operator instead, e.g.:
must be a man). Predicates can also be used with the "exists" quantifier to identify types, but this should usually be done with the "and" operator instead, e.g.: 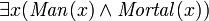 ("there exists something that is both a man and is mortal"). It is easy to write
("there exists something that is both a man and is mortal"). It is easy to write 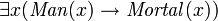 , but this would be equivalent to
, but this would be equivalent to  ("there is something that is not a man, and/or there exists something that is mortal"), which is usually not what was intended. Similarly, assertions can be made that one type is a subtype of another type, e.g.:
("there is something that is not a man, and/or there exists something that is mortal"), which is usually not what was intended. Similarly, assertions can be made that one type is a subtype of another type, e.g.: 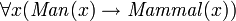 ("for all
("for all 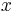 , if
, if 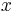 is a man, then
is a man, then 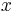 is a mammal").
is a mammal").
Graph reachability cannot be expressed
Many situations can be modeled as a graph of nodes and directed connections (edges). For example, validating many systems requires showing that a "bad" state cannot be reached from a "good" state, and these interconnections of states can often be modelled as a graph. However, it can be proved that connectedness cannot be fully expressed in predicate logic. In other words, there is no predicate-logic formula 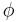 and
and  as its only predicate symbol (of arity 2) such that
as its only predicate symbol (of arity 2) such that 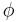 holds in an interpretation
holds in an interpretation 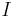 if and only if the extension of
if and only if the extension of  in
in 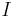 describes a connected graph: that is, connected graphs cannot be axiomatized.
describes a connected graph: that is, connected graphs cannot be axiomatized.
Note that given a binary relation  encoding a graph, one can describe
encoding a graph, one can describe  in terms of a conjunction of first order formulas, and write a formula
in terms of a conjunction of first order formulas, and write a formula 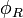 which is satisfiable if and only if
which is satisfiable if and only if  is connected.[10]
is connected.[10]
Comparison with other logics
- Typed first-order logic allows variables and terms to have various types (or sorts). If there are only a finite number of types, this does not really differ much from first-order logic, because one can describe the types with a finite number of unary predicates and a few axioms. Sometimes there is a special type Ω of truth values, in which case formulas are just terms of type Ω.
- First-order logic with domain conditions adds domain conditions (DCs) to classical first-order logic, enabling the handling of partial functions; these conditions can be proven "on the side" in a manner similar to PVS's type correctness conditions. It also adds if-then-else to keep definitions and proofs manageable (they became too complex without them).[11]
- The SMT-LIB Standard defines a language used by many research groups for satisfiability modulo theories; the full logic is based on FOL with equality, but adds sorts (types), if-then-else for terms and formulas (ite() and if.. then.. else..), a let construct for terms and formulas (let and flet), and a distinct construct declaring a set of listed values as distinct. Its connectives are not, implies, and, or, xor, and iff.[12]
- Weak second-order logic allows quantification over finite subsets.
- Monadic second-order logic allows quantification over subsets, that is, over unary predicates.
- Second-order logic allows quantification over subsets and relations, that is, over all predicates. For example, the axiom of extensionality can be stated in second-order logic as x = y ≡def
 P (P(x) ↔ P(y)). The strong semantics of second-order logic give such sentences a much stronger meaning than first-order semantics.
P (P(x) ↔ P(y)). The strong semantics of second-order logic give such sentences a much stronger meaning than first-order semantics. - Higher-order logics allows quantification over higher types than second-order logic permits. These higher types include relations between relations, functions from relations to relations between relations, etc.
- Intuitionistic first-order logic uses intuitionistic rather than classical propositional calculus; for example, ¬¬φ need not be equivalent to φ. Similarly, first-order fuzzy logics are first-order extensions of propositional fuzzy logics rather than classical logic.
- Modal logic has extra modal operators with meanings which can be characterised informally as, for example "it is necessary that φ" and "it is possible that φ".
- In monadic predicate calculus predicates are restricted to having only one argument.
- Infinitary logic allows infinitely long sentences. For example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables. Infinitely long sentences arise in areas of mathematics including topology and model theory.
- First-order logic with extra quantifiers has new quantifiers Qx,..., with meanings such as "there are many x such that ...". Also see branching quantifiers and the plural quantifiers of George Boolos and others.
- Predicate Logic with Definitions (PLD, or D-logic) modifies FOL by formally adding syntactic definitions as a type of value (in addition to formulas and terms); these definitions can be used inside terms and formulas[13].
- Independence-friendly logic is characterized by branching quantifiers, which allow one to express independence between quantified variables.
Most of these logics are in some sense extensions of FOL: they include all the quantifiers and logical operators of FOL with the same meanings. Lindström showed that FOL has no extensions (other than itself) that satisfy both the compactness theorem and the downward Löwenheim–Skolem theorem. A precise statement of Lindström's theorem requires a few technical conditions that the logic is assumed to satisfy; for example, changing the symbols of a language should make no essential difference to which sentences are true.
Algebraizations
Three ways of eliminating quantified variables from FOL, and that do not involve replacing quantifiers with other variable binding term operators, are known:
- Cylindric algebra, by Alfred Tarski and his coworkers;
- Polyadic algebra, by Paul Halmos;
- Predicate functor logic, mainly due to Willard Quine.
These algebras:
- Are all proper extensions of the two-element Boolean algebra, and thus are lattices;
- Do for FOL what Lindenbaum-Tarski algebra does for sentential logic;
- Allow results from abstract algebra, universal algebra, and order theory to be brought to bear on FOL.
Tarski and Givant (1987) show that the fragment of FOL that has no atomic sentence lying in the scope of more than three quantifiers, has the same expressive power as relation algebra. This fragment is of great interest because it suffices for Peano arithmetic and most axiomatic set theory, including the canonical ZFC. They also prove that FOL with a primitive ordered pair is equivalent to a relation algebra with two ordered pair projection functions.
Automation
Theorem proving for first-order logic is one of the most mature subfields of automated theorem proving. The logic is expressive enough to allow the specification of arbitrary problems, often in a reasonably natural and intuitive way. On the other hand, it is still semidecidable, and a number of sound and complete calculi have been developed, enabling fully automated systems. In 1965 J. Alan Robinson achieved an important breakthrough with his resolution approach; to prove a theorem it tries to refute the negated theorem, in a goal-directed way, resulting in a much more efficient method to automatically prove theorems in FOL. More expressive logics, such as higher-order and modal logics, allow the convenient expression of a wider range of problems than first-order logic, but theorem proving for these logics is less well developed.
A modern and particularly disruptive new technology is that of SMT solvers, which add arithmetic and propositional support to the powerful classes of SAT solvers.
See also
- Automated theorem proving
- Cylindric algebra
- Gödel's completeness theorem
- Gödel's incompleteness theorems
- List of first-order theories
- List of rules of inference
- Mathematical logic
- Predicate functor logic
- Table of logic symbols
- Algebra of sets
References
- ↑ The word language is sometimes used as a synonym for signature, but this can be confusing because "language" can also refer to the set of formulas.
- ↑ More precisely, there is only one language of each variant of one-sorted first-order logic: with or without equality, with or without functions, with or without propositional variables, ….
- ↑ When working with first-order logic without identity it may be useful to include a binary predicate symbol = in the signature. The difference between first-order logic with identity and first-order logic without identity, but with = as a non-logical symbol, is that in the latter case there are no special restrictions on the semantics of =. For example there may be two (different) elements between which the relation = holds.
- ↑ For another well-worked example, see Metamath proof explorer
- ↑ Suber, Peter, Translation Tips, http://www.earlham.edu/~peters/courses/log/transtip.htm, retrieved on 2007-09-20
- ↑ Otter Example if.in, http://www-unix.mcs.anl.gov/AR/otter/examples33/fringe/if.in, retrieved on 2007-09-21
- ↑ Manna, Zohar (1974), Mathematical Theory of Computation, McGraw-Hill Computer Science Series, New York, New York: McGraw-Hill Book Company, pp. 77-147, ISBN 0-07-039910-7
- ↑ Leslie Lamport, Lawrence C. Paulson. Should Your Specification Language Be Typed? ACM Transactions on Programming Languages and Systems. 1998. http://citeseer.ist.psu.edu/71125.html
- ↑ Rushby, John. Subtypes for Specification. 1997. Proceedings of the Sixth European Software Engineering Conference (ESEC/FSE 97). http://citeseer.ist.psu.edu/328947.html
- ↑ Huth, Michael; Ryan, Mark (2004), Logic in Computer Science, 2nd edition, pp. 138-139, ISBN 0-521-54310-X
- ↑ Freek Wiedijk and Jan Zwanenburg. "First Order Logic with Domain Conditions" In Theorem Proving in Higher Order Logics. Book Series "Lecture Notes in Computer Science". Springer Berlin / Heidelberg. ISSN 0302-9743 (Print) 1611-3349 (Online), Volume 2758/2003. ISBN 978-3-540-40664-8. http://www.springerlink.com/content/8uh32tu7uf04yeex/
- ↑ Ranise, Silvio and Cesare Tinelli. The SMT-LIB Standard: Version 1.2 Aug 30, 2006. http://smt-lib.org/
- ↑ Makarov, Victor. "Predicate Logic with Definitions". http://arxiv.org/pdf/cs/9906010
- Jon Barwise and John Etchemendy, 2000. Language Proof and Logic. CSLI (University of Chicago Press) and New York: Seven Bridges Press.
- David Hilbert and Wilhelm Ackermann 1950. Principles of Theoretical Logic (English translation). Chelsea. The 1928 first German edition was titled Grundzüge der theoretischen Logik.
- Wilfrid Hodges, 2001, "Classical Logic I: First Order Logic," in Lou Goble, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
External links
- Stanford Encyclopedia of Philosophy: "Classical Logic -- by Stewart Shapiro. Covers syntax, model theory, and metatheory for first-order logic in the natural deduction style.
- forall x: an introduction to formal logic, by P.D. Magnus, covers formal semantics and proof theory for first-order logic.
- Metamath: an ongoing online project to reconstruct mathematics as a huge first-order theory, using first-order logic and the axiomatic set theory ZFC. Principia Mathematica modernized and done right.
- Podnieks, Karl. Introduction to mathematical logic.
- Cambridge Mathematics Tripos Notes : "[1] -- Notes typeset by John Fremlin. The notes cover part of a past Cambridge Mathematics Tripos course taught to undergraduates students (usually) within their third year. The course is entitled "Logic, Computation and Set Theory" and covers Ordinals and cardinals, Posets and zorn’s Lemma, Propositional logic, Predicate logic, Set theory and Consistency issues related to ZFC and other set theories.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||