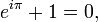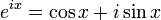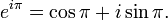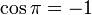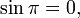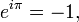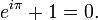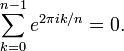Euler's identity

The exponential function ez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 + iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 + iπ/N)N. It can be seen that as N gets larger (1 + iπ/N)N approaches a limit of −1.

  Part of a series of articles on
The mathematical constant, e
Euler's formula.svg

Natural logarithm

Applications in: compound interest · Euler's identity & Euler's formula  · half-lives & exponential growth/decay

Defining e: proof that e is irrational  · representations of e · Lindemann–Weierstrass theorem

People John Napier  · Leonhard Euler

Schanuel's conjecture

In mathematical analysis, Euler's identity, named after Leonhard Euler, is the equation

e^{i \pi} + 1 = 0, \,\!

where

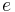e\,\! is Euler's number, the base of the natural logarithm,
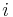i\,\! is the imaginary unit, one of the two complex numbers whose square is negative one (the other is 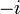-i\,\!), and
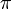\pi\,\! is pi, the ratio of the circumference of a circle to its diameter.

Euler's identity is also sometimes called Euler's equation.

Contents

Nature of the identity

Euler's identity is considered by many to be remarkable for its mathematical beauty. Three basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:

Furthermore, in mathematical analysis, equations are commonly written with zero on one side.

Perceptions of the identity

A reader poll conducted by Mathematical Intelligencer named the identity as the most beautiful theorem in mathematics.[1] Another reader poll conducted by Physics World in 2004 named Euler's identity the "greatest equation ever", together with Maxwell's equations.[2]

The book Dr. Euler's Fabulous Formula [2006], by Paul Nahin (Professor Emeritus at the University of New Hampshire), is devoted to Euler's identity; it is 400 pages long. The book states that the identity sets "the gold standard for mathematical beauty."[3]

Constance Reid claimed that Euler's identity was "the most famous formula in all mathematics."[4]

Gauss is reported to have commented that if this formula was not immediately apparent to a student on being told it, the student would never be a first-class mathematician.[5]

After proving the identity in a lecture, Benjamin Peirce, a noted nineteenth century mathematician and Harvard professor, said, "It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth." [6]

Stanford mathematics professor Keith Devlin says, "Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence."[7]

Derivation

Euler's formula for a general angle.

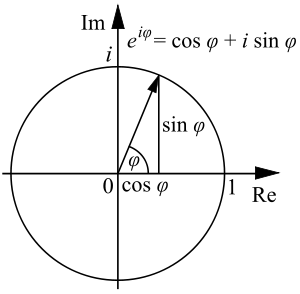
The identity is a special case of Euler's formula from complex analysis, which states that

e^{ix} = \cos x + i \sin x \,\!

for any real number x. (Note that the arguments to the trigonometric functions sin and cos are taken to be in radians.) In particular,

e^{i \pi} = \cos \pi + i \sin \pi.\,\!

Since

\cos \pi = -1 \, \!

and

\sin \pi = 0,\,\!

it follows that

e^{i \pi} = -1,\,\!

which gives the identity

e^{i \pi} +1 = 0.\,\!

Generalization

Euler's identity is a special case of the more general identity that the nth roots of unity, for n > 1, add up to 0:

\sum_{k=0}^{n-1} e^{2 \pi i k/n} = 0 .

Euler's identity is the case where n = 2.

Attribution

While Euler wrote about his formula relating e to cos and sin terms, there is no known record of Euler actually stating or deriving the simplified identity equation itself; moreover, the formula was likely known before Euler.[8] (If so, then this would be an example of Stigler's law of eponymy.) Thus, the question of whether or not the identity should be attributed to Euler is unanswered.

See also

Notes

  1. ↑ Nahin, 2006, p.2–3 (poll published in summer 1990 issue).
  2. ↑ Crease, 2004.
  3. ↑ Cited in Crease, 2007.
  4. ↑ Reid.
  5. ↑ Derbyshire p.210.
  6. ↑ Maor p.160 and Kasner & Newman p.103–104.
  7. ↑ Nahin, 2006, p.1.
  8. ↑ Sandifer.

References