Energy density
Energy density is the amount of energy stored in a given system or region of space per unit volume, or per unit mass, depending on the context, although the latter is more formally specific energy [5]. In some cases it is obvious from context which quantity is most useful: for example, in rocketry, energy per unit mass is the most important parameter, but when studying pressurized gas or magnetohydrodynamics the energy per unit volume is more appropriate. In a few applications (comparing, for example, the effectiveness of hydrogen fuel to gasoline) both figures are appropriate and should be called out explicitly. (Hydrogen has a higher energy density per unit mass than does gasoline, but a much lower energy density per unit volume)
Energy per unit volume has the same physical units as pressure, and in many circumstances is an exact synonym: for example, the energy density of the magnetic field may be expressed as (and behaves as) a physical pressure, and the energy required to compress a gas may be determined by multiplying the pressure of the compressed gas times its change in volume.
Contents |
Energy density in energy storage and in fuel
In energy storage application the energy density relates the mass of an energy store to its stored energy. The higher the energy density, the more energy may be stored or transported for the same amount of mass. In the context of fuel selection, that energy density of a fuel is also called the specific energy of that fuel, though in general an engine using that fuel will yield less energy due to inefficiencies and thermodynamic considerations—hence the specific fuel consumption of an engine will be greater than the reciprocal of the specific energy of the fuel.
The highest density sources of energy are fusion and fission. Fusion includes energy from the sun which will be available for billions of years (in the form of sunlight) but humans have not learned to make our own sustained fusion power sources. Fission of U-235 in nuclear power plants will be available for billions of years because of the vast supply of the element on earth [6]. Coal and petroleum are the current primary energy sources in the U.S. but have a much lower energy density. Burning local biomass fuels supplies household energy needs (cooking fires, oil lamps, etc.) worldwide.
Energy density (how much energy you can carry) does not tell you about energy conversion efficiency (net output per input) or embodied energy (what the energy output costs to provide, as harvesting, refining, distributing, and dealing with pollution all use energy). Like any process occurring on a large scale, intensive energy use creates environmental impacts: for example, global warming, nuclear waste storage, and deforestation are a few of the consequences of supplying our growing energy demands from fossil fuels, nuclear fission, or biomass.
By dividing by 3.6 the figures for megajoules per kilogram can be converted to kilowatt-hours per kilogram. Unfortunately, the useful energy available by extraction from an energy store is always less than the energy put into the energy store, as explained by the laws of thermodynamics. No single energy storage method boasts the best in specific power, specific energy, and energy density. Peukert's Law describes how the amount of energy we get out depends how quickly we pull it out.
Gravimetric and volumetric energy density of some fuels and storage technologies (modified from the Gasoline article):
- Note: Some values may not be precise because of isomers or other irregularities. See Heating value for a comprehensive table of specific energies of important fuels.
True energy densities
This table gives the energy density of a complete system, including all needed oxidisers.
| Storage type | Energy density by mass (MJ/kg) | Energy density by volume (MJ/L) | Peak recovery efficiency % | Practical recovery efficiency % |
|---|---|---|---|---|
| Mass-energy equivalence | 89,876,000,000 | |||
| Binding energy of Helium-4 nucleus | 683,000,000 | 857,000,000,000,000,000,000,000 (8.57x1024) | ||
| Nuclear fusion of hydrogen (energy from the sun) | 645,000,000 | |||
| Deuterium-Tritium fusion | 337,000,000 | |||
| Nuclear fission (of 100% U-235) (Used in nuclear power plants) | 88,250,000 | 1,500,000,000 | ||
| Natural uranium (99.3% U238, 0.7% U235) in fast breeder reactor[7] | 24,000,000 | 50% | ||
| Enriched uranium (3.5% U235) in light water reactor | 3,456,000 | 30% | ||
| Hf-178m2 isomer | 1,326,000 | 17,649,060 | ||
| Natural uranium (0.7% U235) in light water reactor | 443,000 | 30% | ||
| Ta-180m isomer | 41,340 | 689,964 | ||
| Specific orbital energy of Low Earth orbit | 33 (approx.) | |||
| Cl2O7 + CH4 - computed | 17.4 | |||
| Cl2O7 decomposition - computed | 12.2 | |||
| Nitromethane | 11.3 | 12.9 | ||
| Octanitrocubane explosive - computed | 8.5 | 17 | ||
| Tetranitrotetrahedrane explosive - computed | 8.3 | |||
| Heptanitrocubane explosive - computed | 8.2 | |||
| Dinitroacetylene explosive - computed | 7.9 | |||
| Sodium (reacted with chlorine) | 7.0349 | |||
| Tetranitrocubane explosive - computed | 6.95 | |||
| Ammonal (Al+NH4NO3 oxidizer) | 6.9 | 12.7 | ||
| Tetranitromethane + hydrazine bipropellant - computed | 6.6 | |||
| Hexanitrobenzene explosive - computed | 6.5 | |||
| Octogen explosive - computed | 6.3 | |||
| ANFO-ANNM | 6.26 | |||
| TNTin [Kinney, G.F.; K.J. Graham (1985). Explosive shocks in air. Springer-Verlag. ISBN 3-540-15147-8.] | 4.610 | 6.92 | ||
| Copper Thermite (Al + CuO as oxidizer) | 4.13 | 20.9 | ||
| Thermite (powder Al + Fe2O3 as oxidizer) | 4.00 | 18.4 | ||
| Hydrogen peroxide decomposition (as monopropellant) | 2.7 | 3.8 | ||
| Lithium ion battery with nanowires | 2.54-2.72? | 95%[8] | ||
| Lithium thionyl chloride battery [9] | 2.5 | |||
| Water 220.64 bar, 373.8°C | 1.968 | 0.708 | ||
| Kinetic energy penetrator | 1.9-3.4 | 30-54 | ||
| Fluoride ion battery [10] | 1.7-(?) | 2.8(?) | ||
| Regenerative Fuel Cell (fuel cell with internal Hydrogen reservoir used much as a battery) | 1.62 [11] | |||
| Hydrazine(toxic) decomposition (as monopropellant) | 1.6 | 1.6 | ||
| Ammonium nitrate decomposition (as monopropellant) | 1.4 | 2.5 | ||
| Zinc-air battery | 1.33 | |||
| Capacitor by EEStor (claimed prototype capacity) | 1.0 [12] | 2.18 | ||
| Thermal energy storage(Molten Salt) | 1 approx. | |||
| Molecular spring | 1 approx. | |||
| Sodium-sulfur battery | 1.23 [13] | 85%[14] | ||
| Liquid nitrogen | 0.77[1] | 0.62 | ||
| Lithium ion battery[2] | 0.54–0.72 | 0.9–1.9 | 95%[15] | |
| Lithium sulphur battery | 0.54-1.44 | |||
| compressed air at 300 bar (at 12°C), without container | 0.512 | 0.16 | ||
| Flywheel | 0.5 | 81-94% | ||
| 5.56 × 45 mm NATO bullet | 0.4-0.8 | 3.2-6.4 | ||
| Zn-air batteries | 0.40 to 1.7 | 5.9 | ||
| Ice(Ice) | 0.335 | 0.335 | ||
| Zinc-bromine flow battery | 0.27–0.306 [16] | |||
| Compressed air at 20 bar (at 12°C), without container | 0.27 | 0.01 | 64%[17] | |
| NiMH Battery | 0.22 | |||
| NiCd Battery | 0.14-0.22 | 80% [18] | ||
| Lead acid battery | 0.09–0.11 | |||
| Compressed air in fiber-wound bottle at 200 bar (at 24°C) | 0.14 | 0.06 | ||
| Vanadium redox battery | 0.09 [19] | 0.1188 | 70-75% | |
| Vanadium bromide redox battery | 0.18 [20] | 0.252 | 81% | |
| compressed air in steel bottle at 200 bar (at 24°C) | 0.04 | 0.1 | ||
| Capacitor Ultracapacitor | 0.0206 [21] | 0.050 [22] | ||
| Capacitor Supercapacitor | 0.01 | 98.5% | 90%[23] | |
| Capacitor | 0.002 [24] | |||
| Water at 100 m dam height | 0.001 | 0.001 | 85-90%[25] | |
| Spring power (clock spring), torsion spring | 0.0003 [26] | 0.0006 | ||
| Storage type | Energy density by mass (MJ/kg) | Energy density by volume (MJ/L) | Peak recovery efficiency % | Practical recovery efficiency % |
Energy densities excluding oxidisers
This table lists energy densities of fuels that require external oxidisers, such as oxygen. These figures do not take into account the mass and volume of the oxygen required for the chemical reactions, as it is assumed to be freely available and present in the atmosphere. Such systems give a higher energy density than an equivalent system that must hold its own oxidiser.
| Storage type | Energy density by mass (MJ/kg) | Energy density by volume (MJ/L) | Peak recovery efficiency % | Practical recovery efficiency % |
|---|---|---|---|---|
| Liquid hydrogen | 143 | 10.1 | ||
| Compressed gaseous hydrogen at 700 bar [27] | 143 | 5.6 | ||
| Gaseous hydrogen at room temperature | 143 | 0.01079 | ||
| Beryllium (toxic) (burned in air) | 67.6 | 125.1 | ||
| Lithium borohydride (burned in air) | 65.2 | 43.4 | ||
| Boron [28] (burned in air) | 58.9 | 137.8 | ||
| Methane (1.013bar, 15°C) (burned in air) | 55.6 | 0.0378 | ||
| Natural gas (burned in air) | 53.6[3] | 10 | ||
| LPG propane (burned in air)[4] | 49.6 | 25.3 | ||
| LPG butane (burned in air)[4] | 49.1 | 27.7 | ||
| Gasoline[4] | 46.4 | 34.2 | ||
| Diesel fuel/residential heating oil (burned in air)[4] | 46.2 | 37.3 | ||
| Polyethylene plastic | 46.3[5] | 42.6 | ||
| Polypropylene plastic | 46.4[5] | 41.7 | ||
| Gasohol E10 (10% ethanol 90% gasoline by volume) | 43.54 | 33.72 | ||
| Gasohol E85 (85% ethanol 10% gasoline by volume) | 33.1 | 25.65 | ||
| Lithium (burned in air) | 43.1 | 23.0 | ||
| Jet A aviation fuel [29] / kerosene | 42.8 | 33 | ||
| Biodiesel oil (vegetable oil) | 42.20 | 33 | ||
| DMF (2,5-dimethylfuran) | 42 [30] | 37.8 | ||
| Crude oil (according to the definition of ton of oil equivalent) | 46.3 | 37[3] | ||
| Polystyrene plastic | 41.4[5] | 43.5 | ||
| Body fat metabolism | 38 | 35 | 22-26%[31] | |
| Butanol | 36.6 | 29.2 | ||
| Graphite (burned in air) | 32.7 | 72.9 | ||
| coal Anthracite | 32.5 | 72.4 | 36% | |
| Silicon (burned in air)[32] | 32.2 | 75.1 | ||
| Aluminum (burned in air) | 31.0 | 83.8 | ||
| Ethanol | 30 | 24 | ||
| Polyester plastic | 26.0 [5] | 35.6 | ||
| Magnesium (burned in air) | 24.7 | 43.0 | ||
| coal Bituminous [33] | 24 | 20 | ||
| PET plastic | 23.5 (impure) [34] | |||
| Methanol | 19.7 | 15.6 | ||
| Hydrazine (toxic) combusted to N2+H2O | 19.5 | 19.3 | ||
| Liquid ammonia (combusted to N2+H2O) | 18.6 | 11.5 | ||
| PVC plastic (improper combustion toxic) | 18.0[5] | 25.2 | ||
| Sugars, carbohydrates & protein metabolism | 17 | 26.2(dextrose) | 22-26% [35] | |
| coal Lignite | 14.0 (to 19) | |||
| Calcium (burned in air) | 15.9 | 24.6 | ||
| Glucose | 15.55 | 23.9 | ||
| Dry cowdung and cameldung | 15.5 [36] | |||
| Wood | 6.0 (to 17) | |||
| Sodium (burned to wet sodium hydroxide) | 13.3 | 12.8 | ||
| Household waste | 8.0 (to 11)[6][7] | |||
| Sodium (burned to dry sodium oxide) | 9.1 | 8.8 | ||
| Zinc (burned in air) | 5.3 | 38.0 | ||
| Teflon plastic (combustion toxic, but flame retardant) | 5.1 | 11.2 | ||
| iron (burned to iron(III) oxide) | 5.2 | 40.68 | ||
| iron (burned to iron(II) oxide) | 4.9 | 38.2 | ||
| Storage type | Energy density by mass (MJ/kg) | Energy density by volume (MJ/L) | Peak recovery efficiency % | Practical recovery efficiency % |
Energy density of electric and magnetic fields
Electric and magnetic fields store energy. In a vacuum, the (volumetric) energy density (in SI units) is given by
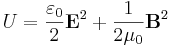 ,
,
where E is the electric field and B is the magnetic field. In the context of magnetohydrodynamics, the physics of conductive fluids, the magnetic energy density behaves like an additional pressure that adds to the gas pressure of a plasma.
In normal (linear) substances, the energy density (in SI units) is
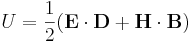 ,
,
where D is the electric displacement field and H is the magnetizing field.
Energy density of empty space
In physics, "vacuum energy" or "zero-point energy" is the volumetric energy density of empty space. More recent developments have expounded on the concept of energy in empty space.
Modern physics is commonly classified into two fundamental theories: quantum field theory and general relativity. Quantum field theory takes quantum mechanics and special relativity into account, and it's a theory of all the forces and particles except gravity. General relativity is a theory of gravity, but it is incompatible with quantum mechanics. Currently these two theories have not yet been reconciled into one unified description, though research into "quantum gravity" seeks to bridge this divide.
In general relativity, the cosmological constant is proportional to the energy density of empty space, and can be measured by the curvature of space. It is subsequently related to the age of the universe, and as energy expands outwards with time its density changes.
Quantum field theory considers the vacuum ground state not to be completely empty, but to consist of a seething mass of virtual particles and fields. These fields are quantified as probabilities—that is, the likelihood of manifestation based on conditions. Since these fields do not have a permanent existence, they are called vacuum fluctuations. In the Casimir effect, two metal plates can cause a change in the vacuum energy density between them which generates a measurable force.
Some believe that vacuum energy might be the "dark energy" (also called Quintessence) associated with the cosmological constant in general relativity, thought to be similar to a negative force of gravity (or antigravity). Observations that the expanding universe appears to be accelerating seem to support the cosmic inflation theory—first proposed by Alan Guth in 1981—in which the nascent universe passed through a phase of exponential expansion driven by a negative vacuum energy density (positive vacuum pressure).
Energy density of food
Energy density is the amount of energy (kilojoules or calories) per amount of food, with food amount being measured in grams or milliliters of food. Energy density is thus expressed in cal/g, kcal/g, J/g, kJ/g, cal/mL, kcal/mL, J/mL, or kJ/mL. This is the energy released when the food is metabolised by a healthy organism when it ingests the food (see food energy for calculation) and the food is metabolized with oxygen, into waste products such as carbon dioxide and water. Typical values of food energy density for high energy-density foods, such as a hamburger, would be 2.5 kcal/g. Purified fats and oils contain the highest energy densities—about 9 kcal/g. What is popularly referred to as the number of "Calories" in a portion of food (invariably spelled with a capital C to show that it is the food Calorie) is therefore the number of kilocalories (thousands of calories with the small c) in the portion.
Miscellaneous
- Kinetic energy per unit mass:
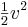 J/kg, where v is the speed in m/s. See also kinetic energy per unit mass of projectiles.
J/kg, where v is the speed in m/s. See also kinetic energy per unit mass of projectiles. - Potential energy with respect to gravity, close to earth, per unit mass: ca. 9.8 h J/kg, with h the height in m.
- Heat: energies per unit mass are specific heat capacity times temperature difference, and specific melting heat, and specific heat of vaporization
See also
- Figure of merit
- Energy content of biofuel
- Heat of combustion
- Heating value
- Rechargeable battery
- Specific impulse
- Vacuum energy
External references
Zero point energy
- Eric Weisstein's world of physics: energy density [37]
- Baez physics: Is there a nonzero cosmological constant? [38]; What's the Energy Density of the Vacuum?.
- Introductory review of cosmic inflation [39]
- An exposition to inflationary cosmology [40]
Density data
- ^ "Aircraft Fuels." Energy, Technology and the Environment Ed. Attilio Bisio. Vol. 1. New York: John Wiley and Sons, Inc., 1995. 257-259
- “Fuels of the Future for Cars and Trucks” - Dr. James J. Eberhardt - Energy Efficiency and Renewable Energy, U.S. Department of Energy - 2002 Diesel Engine Emissions Reduction (DEER) Workshop San Diego, California - August 25 - 29, 2002
Energy storage
Books
- The Inflationary Universe: The Quest for a New Theory of Cosmic Origins by Alan H. Guth (1998) ISBN 0-201-32840-2
- Cosmological Inflation and Large-Scale Structure by Andrew R. Liddle, David H. Lyth (2000) ISBN 0-521-57598-2
- Richard Becker, "Electromagnetic Fields and Interactions", Dover Publications Inc., 1964
Footnotes
- ↑ C. Knowlen, A.T. Mattick, A.P. Bruckner and A. Hertzberg, "High Efficiency Conversion Systems for Liquid Nitrogen Automobiles", Society of Automotive Engineers Inc, 1988.
- ↑ A typically available lithium ion cell with an Energy Density of 201 wh/kg [1]
- ↑ 3.0 3.1 Envestra Limited. Natural Gas. Retrieved 2008-10-05
- ↑ 4.0 4.1 4.2 4.3 IOR Energy. List of common conversion factors (Engineering conversion factors). Retrieved 2008-10-05
- ↑ 5.0 5.1 5.2 5.3 5.4 [2]
- ↑ [3]
- ↑ [4]