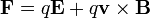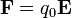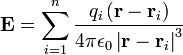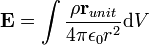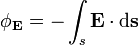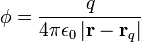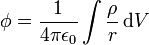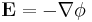Classical electromagnetism

Electromagnetism

Electrostatics
· Electric charge · Coulomb’s law · Electric field · Electric flux · Gauss’ law · Electric potential · Electrostatic induction · Electric dipole moment ·

Magnetostatics
· Ampère’s law · Electric current · Magnetic field · Magnetic flux · Biot–Savart law · Magnetic dipole moment · Gauss’s law for magnetism ·

Electrodynamics
· Free space · Lorentz force law · EMF · Electromagnetic induction · Faraday’s law · Displacement current · Maxwell’s equations · EM field · Electromagnetic radiation · Liénard-Wiechert Potentials · Maxwell tensor · Eddy current ·

Electrical Network
· Electrical conduction · Electrical resistance · Capacitance · Inductance · Impedance · Resonant cavities · Waveguides ·

Covariant formulation
· Electromagnetic tensor · EM Stress-energy tensor · Four-current · Four-potential ·

Scientists
· Ampère · Coulomb · Faraday · Heaviside · Henry · Hertz · Lorentz · Maxwell · Tesla · Weber ·

Classical electromagnetism (or classical electrodynamics) is a theory of electromagnetism that was developed over the course of the 19th century, most prominently by James Clerk Maxwell. It provides an excellent description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible (see quantum electrodynamics).

Maxwell's equations and the Lorentz force law form the basis for the theory of classical electromagnetism.

1 Lorentz force
2 The electric field E
3 Electromagnetic waves
4 General field equations
5 See also

Lorentz force

Main article: Lorentz force

The electromagnetic field exerts the following force (often called the Lorentz force) on charged particles:

$\mathbf{F} = q\mathbf{E} + q\mathbf{v} \times \mathbf{B}$

where all boldfaced quantities are vectors: F is the force that a charge q experiences, E is the electric field at q's location, v is q's velocity, B is the magnetic field at q's position.

The electric field E

Main article: Electric field

The electric field E is defined such that, on a stationary charge:

$\mathbf{F} = q_0 \mathbf{E}$

where q₀ is what is known as a test charge. The size of the charge doesn't really matter, as long as it is small enough as to not influence the electric field by its mere presence. What is plain from this definition, though, is that the unit of E is N/C, or newtons per coulomb. This unit is equal to V/m (volts per meter), see below.

The above definition seems a little bit circular but, in electrostatics, where charges are not moving, Coulomb's law works fine. So what we end up with is:

$\mathbf{E} = \sum_{i=1}^{n} \frac{q_i \left( \mathbf{r} - \mathbf{r}_i \right)} {4 \pi \epsilon_0 \left| \mathbf{r} - \mathbf{r}_i \right|^3}$

where n is the number of charges, q_i is the amount of charge associated with the 'i'th charge, r_i is the position of the 'i'th charge, r is the position where the electric field is being determined, and ε₀ is a universal constant called the permittivity of free space.

Note: the above is just Coulomb's law, divided by q₁, adding up multiple charges.

Changing the summation to an integral yields the following:

$\mathbf{E} = \int \frac{\rho \mathbf{r}_{unit}}{ 4 \pi \epsilon_0 r^2} \mathrm{d}V$

where ρ is the charge density as a function of position, r_unit is the unit vector pointing from dV to the point in space E is being calculated at, and r is the distance from the point E is being calculated at to the point charge.

Both of the above equations are cumbersome, especially if one wants to calculate E as a function of position. There is, however, a scalar function called the electrical potential that can help. Electric potential, also called voltage (the units for which are the volt), which is defined thus:

$\phi_\mathbf{E} = - \int_s \mathbf{E} \cdot \mathrm{d}\mathbf{s}$

where φ_E is the electric potential, and s is the path over which the integral is being taken.

Unfortunately, this definition has a caveat. From Maxwell's equations, it is clear that 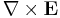$\nabla \times \mathbf{E}$ is not always zero, and hence the scalar potential alone is insufficient to define the electric field exactly. As a result, one must resort to adding a correction factor, which is generally done by subtracting the time derivative of the A vector potential described below. Whenever the charges are quasistatic, however, this condition will be essentially met, so there will be few problems. (As a side note, by using the appropriate gauge transformations, one can define V to be zero and define E entirely as the negative time derivative of A, however, this is rarely done because a) it's a hassle and more important, b) it no longer satisfies the requirements of the Lorenz gauge and hence is no longer relativistically invariant).

From the definition of charge, it is trivial to show that the electric potential of a point charge as a function of position is:

$\phi = \frac{q}{ 4 \pi \epsilon_0 \left| \mathbf{r} - \mathbf{r}_q \right|}$

where q is the point charge's charge, r is the position, and r_q is the position of the point charge. The potential for a general distribution of charge ends up being:

$\phi = \frac{1}{4 \pi \epsilon_0} \int \frac{\rho}{r}\, \mathrm{d}V$

where ρ is the charge density as a function of position, and r is the distance from the volume element 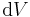$\mathrm{d}V$ .

Note well that φ is a scalar, which means that it will add to other potential fields as a scalar. This makes it relatively easy to break complex problems down in to simple parts and add their potentials. Taking the definition of φ backwards, we see that the electric field is just the negative gradient (the del operator) of the potential. Or:

$\mathbf{E} = -\nabla \phi$

From this formula it is clear that E can be expressed in V/m (volts per meter).

Electromagnetic waves

Main article: Electromagnetic waves

A changing electromagnetic field propagates away from its origin in the form of a wave. These waves travel in vacuum at the speed of light and exist in a wide spectrum of wavelengths. Examples of the dynamic fields of electromagnetic radiation (in order of increasing frequency): radio waves, microwaves, light (infrared, visible light and ultraviolet), x-rays and gamma rays. In the field of particle physics this electromagnetic radiation is the manifestation of the electromagnetic interaction between charged particles.

General field equations

Main articles: Jefimenko's equations and Liénard-Wiechert Potentials

As simple and satisfying as Coulomb's equation may be, it is not entirely correct in the context of classical electromagnetism. Problems arise because changes in charge distributions require a non-zero amount of time to be "felt" elsewhere (required by special relativity). Disturbances of the electric field due to a charge propagate at the speed of light.

For the fields of general charge distributions, the retarded potentials can be computed and differentiated accordingly to yield Jefimenko's Equations.

Retarded potentials can also be derived for point charges, and the equations are known as the Liénard-Wiechert potentials. The scalar potential is:

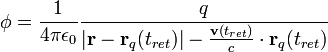
$\phi = \frac{1}{4 \pi \epsilon_0} \frac{q}{\left| \mathbf{r} - \mathbf{r}_q(t_{ret}) \right|-\frac{\mathbf{v}(t_{ret})}{c} \cdot \mathbf{r}_q(t_{ret})}$

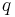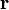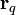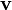where $q$ is the point charge's charge and $\mathbf{r}$ is the position. $\mathbf{r}_q$ and $\mathbf{v}$ are the position and velocity of the charge, respectively, as a function of retarded time. The vector potential is similar:

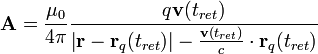
$\mathbf{A} = \frac{\mu_0}{4 \pi} \frac{q\mathbf{v}(t_{ret})}{\left| \mathbf{r} - \mathbf{r}_q(t_{ret}) \right|-\frac{\mathbf{v}(t_{ret})}{c} \cdot \mathbf{r}_q(t_{ret})}$

These can then be differentiated accordingly to obtain the complete field equations for a moving point particle.

Classical electromagnetism

Contents

Lorentz force

The electric field E

Electromagnetic waves

General field equations

See also