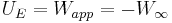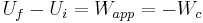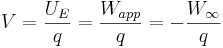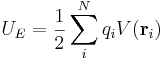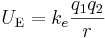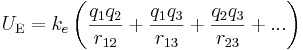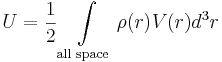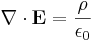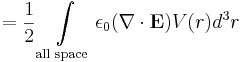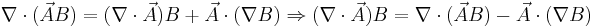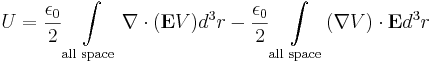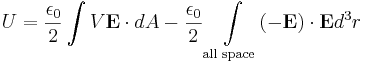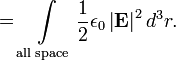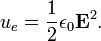Electric potential energy

Electric energy is the potential energy associated with the conservative Coulomb forces between charged particles contained within a system, where the reference potential energy is usually chosen to be zero for particles at infinite separation.^[1]^:§25-1 It can be defined as the amount of work one must apply to (massless) charged particles to bring them from infinite separation to some finite proximity configuration. This is also equal to the negative of the work of the Coulomb forces that the particles exert on each other during the quasistatic move:^[1]^:§25-1

$U_E = W_{app} = - W_\infty$

where

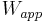$W_{app} \$ is the work required to bring the system to a certain finite proximity configuration. "app" stands for applied, because this is work that must be applied to the system (or be supplied by another form of energy contained by the system) to configure it
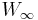$W_\infty \$ is the work done by electrostatic inter-particle Coulomb forces during the move from infinity.

Sometimes people refer to the potential energy of a charge in an electric field. This actually refers to the potential energy of the system containing the charge and the other particles that created the electric field.^[1]^:§25-1

Furthermore, to calculate the work required to bring a charged particle into the vicinity of other particles, it is sufficient to know only the field generated by the other particles and the charge of the particle being moved. The field of the moving particle and the individual charges of the other particles do not need to be known.

Finally, it must be stressed that, even though this article talks about moving particles, the Coulomb force law on which this discussion is based only holds in the case of electrostatic systems. Therefore, any movement would have to be a quasistatic process.

1 Properties
2 Potential energy stored in a configuration of discrete charges
3 Potential energy of a continuous charge distribution
4 Energy stored in an electric field
5 See also
6 References

Properties

Since Coulomb forces are conservative, change in electric potential energy is independent of the path the system takes between two configurations. Correspondingly, the work done by the forces is also path independent and gives the change in electric potential energy:^[1]^:§25-1 The SI unit for work is the Joule.

$U_f-U_i = W_{app} = - W_c \$

where

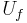$U_f \$ is the electric potential energy at the final state
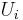$U_i \$ is the electric potential energy at the initial state
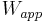$W_{app} \$ is the work required to bring the system to the final state from the initial state
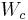$W_c \$ is the work done by inter-particle Coulomb forces during the move

The usual choice of datum is 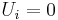$U_i = 0$ at infinite particle separation, as stated in the opening.

Due to the proportionality of the Coulomb force with the charges of the particles on which it acts, the potential energy of a charged particle in a given electric field is also proportional to the charge of the particle. So, the potential energy may be normalized by the charge of the particle on which the field acts to give a quantity called the electric potential, which is only a function of the strength of the electric field (and the particle location):^[1]^:§25-1

$V = \frac {U_E}{q} = \frac {W_{app}}{q} = - \frac {W_\infty}{q}$

where

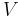$V \$ is the electric potential of the field
$q \$ is the charge of the particle in the field

The above equation is the definition of electric potential for a system (with a datum of zero potential energy at infinite particle separation). It is very important to note that the electric field under consideration is not the total field, but the field due only to all particles except the one at the location for which the electric potential energy (and thus electric potential) is calculated.

Potential energy stored in a configuration of discrete charges

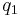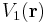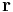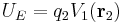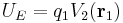The potential energy between two charges is equal to the potential energy of one charge in the electric field of the other. That is to say, if $q_1$ generates a scalar electric potential field $V_1(\mathbf r)$ , which is a function of position $\mathbf r$ , then $U_E = q_2 V_1(\mathbf r_2)$ . Also, a similar development gives $U_E = q_1 V_2(\mathbf r_1)$ .

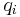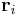This can be generalized to give an expression for a group of N charges, $q_i$ at positions $\mathbf r_i$ :

$U_E = \frac{1}{2}\sum_i^N q_i V(\mathbf r_i)$

where 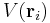$V(\mathbf r_i)$ refers to the electric field due to all particles except the one at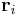 $\mathbf r_i$

Note: The factor of one half accounts for the 'double counting' of charge pairs. For example, consider the case of just two charges.

Alternatively, the factor of one half may be dropped if the sum is only performed once per particle pair. This is done in the examples below to cut down on the math.

One charged particle

The electric potential energy of a system containing only one point charge is zero, as no energy is required to move the charge particle from infinity to its location.

Two charged particles

Consider bringing a second charge into position:

$U_\mathrm{E} = k_e \frac{q_1 q_2}{r}$

where

k_e is Coulomb's constant

q₁, q₂ are the two charges

r is the distance between the two particles

The electric potential energy will be negative if the charges have opposite sign and positive if the charges have the same sign. This simply means that potential energy is lost by a system of opposite charges moving together, which can be explained as 'opposite charges attract'.

Three or more charged particles

For 3 or more point charges, the electric potential energy of the system may be calculated by bringing individual charges into position one after another, and taking the sum of energy required to bring the additional charge into position.

$U_\mathrm{E} = k_e \left({\frac{q_1 q_2}{r_{12}}} + {\frac{q_1 q_3}{r_{13}}} + {\frac{q_2 q_3}{r_{23}}} + ...\right)$

where

k_e is Coulomb's constant

q₁, q₂, ..., are the charges

r_mn is the distance between two particles, m and n (e.g. r₁₂).

Potential energy of a continuous charge distribution

The previous equation can again be generalized to give an expression of the potential energy of a continuous charge distribution.

$U = \frac{1}{2}\int \limits_{\text{all space}} \rho(r)V(r)d^3r$

where:

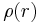$\rho(r)$ is the charge density of the distribution.

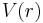$V(r)$ is the electric potential at position r.

Energy stored in an electric field

One may take the equation for the potential energy of a continuous charge distribution and put it in terms of the electric field.

Since Gauss' law for electric field in differential form states

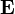$\mathbf{\nabla}\cdot\mathbf{E} = \frac{\rho}{\epsilon_0}$

where

$\mathbf{E} \$ is the electric field vector
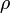$\rho \$ is the total charge density including dipole charges bound in a material
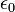$\epsilon_0 \$ is the vacuum permittivity.

then,

$U = \frac{1}{2}\int \limits_{\text{all space}} \rho(r)V(r)d^3r$

$= \frac{1}{2}\int \limits_{\text{all space}} \epsilon_0(\mathbf{\nabla}\cdot{\mathbf{E}})V(r)d^3r$

so, now using the following divergence vector identity

$\nabla\cdot(\vec{A}{B}) = (\nabla\cdot\vec{A}){B} + \vec{A}\cdot(\nabla{B}) \Rightarrow (\nabla\cdot\vec{A}){B} = \nabla\cdot(\vec{A}{B}) - \vec{A}\cdot(\nabla{B})$

we have

$U = \frac{\epsilon_0}{2}\int \limits_{\text{all space}} \mathbf{\nabla}\cdot(\mathbf{E}V) d^3r - \frac{\epsilon_0}{2}\int \limits_{\text{all space}} (\mathbf{\nabla}V)\cdot\mathbf{E} d^3r$

using the divergence theorem and taking the area to be at infinity where 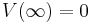$V(\infty) = 0$

$U = \frac{\epsilon_0}{2}\int V\mathbf{E}\cdot dA - \frac{\epsilon_0}{2}\int \limits_{\text{all space}} (-\mathbf{E})\cdot\mathbf{E} d^3r$

$= \int \limits_{\text{all space}} \frac{1}{2}\epsilon_0\left|{\mathbf{E}}\right|^2 d^3r.$

So, the energy density, or energy per unit volume of the electric field is:

$u_e = \frac{1}{2} \epsilon_0 \mathbf{E}^2.$

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 Halliday, David; Resnick, Robert; Walker, Jearl (1997) (in English). Fundamentals of Physics (5th ed.). John Wiley & Sons. ISBN 0-471-10559-7.

Electric potential energy

Contents

Properties

Potential energy stored in a configuration of discrete charges

One charged particle

Two charged particles

Three or more charged particles

Potential energy of a continuous charge distribution

Energy stored in an electric field

See also

References