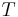Eccentricity (mathematics)

In mathematics, the eccentricity, denoted e or 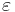 , is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.
, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.
In particular,
- The eccentricity of a circle is zero.
- The eccentricity of an (non-circle) ellipse is greater than zero but less than 1.
- The eccentricity of a parabola is 1.
- The eccentricity of a hyperbola is greater than 1.
Furthermore, two conic sections are similar if and only if they have the same eccentricity.
Contents |
Definitions
For every conic section, there exist a fixed point F, a fixed line L and a non-negative number e such that the conic section consists of all points whose distance to F equals e times their distance to L. e is called the eccentricity of the conic section.
The linear eccentricity of a conic section, denoted c or e, is the distance between its center and its focus (or one of its two foci).
Alternative Names
The eccentricity is sometimes called first eccentricity to distinguish it from the second eccentricity and third eccentricity defined for ellipses (see below). The eccentricity is also sometimes called numerical eccentricity.
In the case of ellipses and hyperbolas the linear eccentricity is sometimes called half-focal separation.
Notation
Two notational conventions are in common use:
- e for the eccentricity and c for the linear eccentricity.
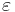 for the eccentricity and e for the linear eccentricity.
for the eccentricity and e for the linear eccentricity.
We will use the first notation in this article.
Values
| conic section | equation | eccentricity (e) | linear eccentricity (c) |
|---|---|---|---|
| circle | 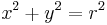 |
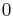 |
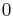 |
| ellipse |  |
 |
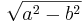 |
| parabola | 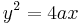 |
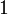 |
 |
| hyperbola | 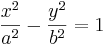 |
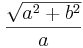 |
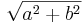 |
Ellipses
For any ellipse, let a be the length of its semi-major axis and b be the length of its semi-minor axis.
We define a number of related additional concepts (only for ellipses):
| name | symbol | value in terms of a and b | value in terms of 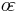 |
|---|---|---|---|
| first eccentricity | 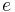 |
 |
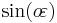 |
| second eccentricity | 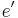 |
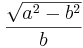 |
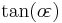 |
| third eccentricity | 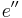 |
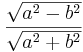 |
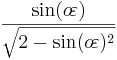 |
| angular eccentricity | 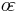 |
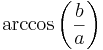 |
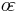 |
Quadrics
The eccentricity of a three-dimensional quadric is the eccentricity of a designated section of it. For example, on a triaxial ellipsoid, the meridional eccentricity is that of the ellipse formed by a section containing both the longest and the shortest axes (one of which will be the polar axis), and the equatorial eccentricity is the eccentricity of the ellipse formed by a section through the centre, perpendicular to the polar axis (i.e. in the equatorial plane).
Celestial Mechanics
In celestial mechanics, for bound orbits in a spherical potential, the definition above is informally generalized. When the apocentre distance is close to pericentre distance, the orbit is said to have low eccentricity; when they are very different, the orbit is said be eccentric or having eccentricity near unity. This definition coincides with the mathematical definition of eccentricity for ellipse, in Keplerian, i.e., 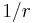 potentials.
potentials.
See also
- Eccentricity vector
- Orbital eccentricity
External links
|
||||||||||||||||||||||||||||||||||||||||||||||
 Longitude of the ascending node
Longitude of the ascending node
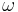
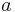 Semi-major axis
Semi-major axis Mean anomaly at
Mean anomaly at 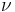 True anomaly
True anomaly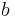 Semi-minor axis
Semi-minor axis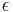 Linear eccentricity
Linear eccentricity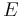 Eccentric anomaly
Eccentric anomaly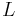 Mean longitude
Mean longitude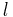 True longitude
True longitude