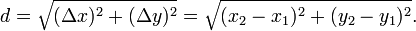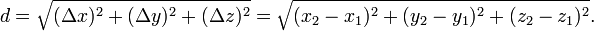Distance

This article is about distance in the mathematical or physical sense. For other senses of the term, see distance (disambiguation).

Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, a period of time, or an estimation based on other criteria (e.g. "two counties over"). In mathematics, distance must meet more rigorous criteria.

In most cases there is symmetry and "distance from A to B" is interchangeable with "distance between B and A".

Contents

Mathematics

See also: Metric (mathematics)

Geometry

In neutral geometry, the minimum distance between two points is the length of the line segment between them.

In analytic geometry, the distance between two points of the xy-plane can be found using the distance formula. The distance between (x1, y1) and (x2, y2) is given by

d=\sqrt{(\Delta x)^2+(\Delta y)^2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}.\,

Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-space, the distance between them is

d=\sqrt{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}.

Which is easily proven by constructing a right triangle with a leg on the hypotenuse of another (with the other leg orthogonal to the plane that contains the 1st triangle) and applying the Pythagorean theorem.

In the study of complicated geometries, we call this (most common) type of distance Euclidean distance, as it is derived from the Pythagorean theorem, which does not hold in Non-Euclidean geometries. This distance formula can also be expanded into the arc-length formula.

Distance in Euclidean space

In the Euclidean space Rn, the distance between two points is usually given by the Euclidean distance (2-norm distance). Other distances, based on other norms, are sometimes used instead.

For a point (x1, x2, ...,xn) and a point (y1, y2, ...,yn), the Minkowski distance of order p (p-norm distance) is defined as:

1-norm distance 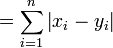= \sum_{i=1}^n \left| x_i - y_i \right|
2-norm distance = \left( \sum_{i=1}^n \left| x_i - y_i \right|^2 \right)^{1/2}
p-norm distance 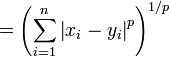= \left( \sum_{i=1}^n \left| x_i - y_i \right|^p \right)^{1/p}
infinity norm distance = \lim_{p \to \infty} \left( \sum_{i=1}^n \left| x_i - y_i \right|^p \right)^{1/p}
= \max \left(|x_1 - y_1|, |x_2 - y_2|, \ldots, |x_n - y_n| \right).

p need not be an integer, but it cannot be less than 1, because otherwise the triangle inequality does not hold.

The 2-norm distance is the Euclidean distance, a generalization of the Pythagorean theorem to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler: the "intuitive" idea of distance.

The 1-norm distance is more colourfully called the taxicab norm or Manhattan distance, because it is the distance a car would drive in a city laid out in square blocks (if there are no one-way streets).

The infinity norm distance is also called Chebyshev distance. In 2D it represents the distance kings must travel between two squares on a chessboard.

The p-norm is rarely used for values of p other than 1, 2, and infinity, but see; super ellipse.

In physical space the Euclidean distance is in a way the most natural one, because in this case the length of a rigid body does not change with rotation.

General case

In mathematics, in particular geometry, a distance function on a given set M is a function d: M×M → R, where R denotes the set of real numbers, that satisfies the following conditions:

Such a distance function is known as a metric. Together with the set, it makes up a metric space.

For example, the usual definition of distance between two real numbers x and y is: d(x,y) = |x − y|. This definition satisfies the three conditions above, and corresponds to the standard topology of the real line. But distance on a given set is a definitional choice. Another possible choice is to define: d(x,y) = 0 if x = y, and 1 otherwise. This also defines a metric, but gives a completely different topology, the "discrete topology"; with this definition numbers cannot be arbitrarily close.

Distances between sets and between a point and a set

d(A,B)>d(A,C)+d(C,B)

Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a LEO, the first tends to be quoted (altitude), otherwise, e.g. for the Earth-Moon distance, the latter.

There are two common definitions for the distance between two non-empty subsets of a given set:

The distance between a point and a sethttp://localhost../../../../articles/m/e/t/Metric_space.html#Distance_between_points_and_sets is the infimum of the distances between the point and those in the set. This corresponds to the distance, according to the first-mentioned definition above of the distance between sets, from the set containing only this point to the other set.

In terms of this, the definition of the Hausdorff distance can be simplified: it is the larger of two values, one being the supremum, for a point ranging over one set, of the distance between the point and the set, and the other value being likewise defined but with the roles of the two sets swapped.

Graph theory

In graph theory the distance between two vertices is the length of the shortest path between those vertices.

Distance versus directed distance and displacement

Distance along a path compared with displacement

Distance cannot be negative. Distance is a scalar quantity, containing only a magnitude, whereas a displacement vector are vector quantities characterized by both magnitude and direction.

The distance covered by a vehicle (often recorded by an odometer), person, animal, or object along a curved path from a point A to a point B should be distinguished from the respective displacement (the distance along a straight line from A to B). For instance, the distance covered during a round trip from A to B and back to A may be very long, while the displacement is always zero (because starting and ending points coincide).

Directed distance

Directed distances are distances with a direction or sense. They can be determined along straight lines and along curved lines. A directed distance along a straight line from A to B is a vector joining any two points in a n-dimensional Euclidean vector space. A directed distance along a curved line is not a vector and is represented by a segment of that curved line defined by endpoints A and B, with some specific information indicating the sense (or direction) of an ideal or real motion from one endpoint of the segment to the other (see figure). For instance, just labelling the two endpoints as A and B can indicate the sense, if the ordered sequence (A, B) is assumed, which implies that A is the starting point.

A displacement (see above) is a special kind of directed distance defined in mechanics. A directed distance is called displacement when it is the distance along a straight line (minimum distance) from A and B, and when A and B are positions occupied by the same particle at two different instants of time. This implies motion of the particle.

Another kind of directed distance is that between two different particles or point masses at a given time. For instance, the distance from the center of gravity of the Earth A and the center of gravity of the Moon B (which does not strictly imply motion from A to B).

Other "distances"

See also

  • Taxicab geometry
  • astronomical units of length
  • cosmic distance ladder
  • comoving distance
  • distance geometry
  • distance (graph theory)
  • Distance in military affairs
  • Dijkstra's algorithm
  • distance-based road exit numbers
  • Distance Measuring Equipment (DME)
  • great-circle distance
  • length
  • milestone
  • Metric (mathematics)
  • Metric space
  • orders of magnitude (length)
  • Proper length
  • distance matrix
  • Hamming distance
  • Free Euclidian distance
  • Lee distance
  • proxemics - physical distance between people

References