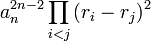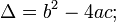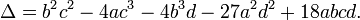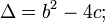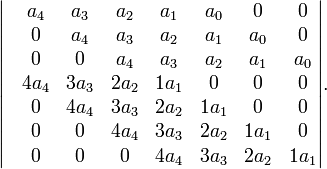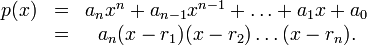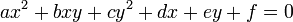Discriminant

In algebra, the discriminant of a polynomial with real or complex coefficients is a certain expression in the coefficients of the polynomial which is equal to zero if and only if the polynomial has a multiple root (i.e. a root with multiplicity greater than one) in the complex numbers. For example, the discriminant of the quadratic polynomial

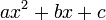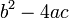$ax^2+bx+c\,$ is $\,b^2-4ac$ .

The discriminant of the cubic polynomial

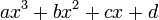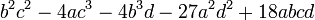$ax^3+bx^2+cx+d\,$ is $\,b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd$ .

This concept also applies if the polynomial has coefficients in a field which is not contained in the complex numbers. In this case, the discriminant vanishes if and only if the polynomial has a multiple root in its splitting field. The discriminant is given by

$a_n^{2n-2}\prod_{i<j}{(r_i-r_j)^2}$

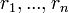where $a_n$ is the leading coefficient and $r_1, ..., r_n$ are the roots (counting multiplicity) of the polynomial in some splitting field.

The concept of discriminant has been generalized to other algebraic structures besides polynomials, including conic sections, quadratic forms, and algebraic number fields. Discriminants in algebraic number theory are closely related, and contain information about ramification. In fact, the more geometric types of ramification are also related to more abstract types of discriminant, making this a central algebraic idea in many applications.

1 Formula
2 Quadratic formula
3 Discriminant of a polynomial
4 Discriminant of a conic section
5 Discriminant of a quadratic form
6 Discriminant of an algebraic number field
7 Discriminant of a differentiable function
8 External links

Formula

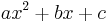The quadratic polynomial $ax^2+bx+c$ has discriminant

$\Delta=b^2-4ac;\,$

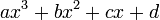the cubic polynomial $ax^3+bx^2+cx+d$ has discriminant

$\Delta=b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd.\,$

Simpler polynomials have simpler expressions for their discriminants. For example,

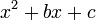the monic quadratic polynomial $x^2+bx+c$ has discriminant

$\Delta=b^2-4c;\,$

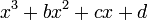the monic cubic polynomial $x^3+bx^2+cx+d$ has discriminant

$\Delta=b^2c^2-4c^3-4b^3d-27d^2+18bcd;\,$

the monic cubic polynomial without quadratic term 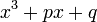$x^3+px+q$ has discriminant

$\Delta=-4p^3-27q^2.\,$

Quadratic formula

The quadratic polynomial P(x) = ax² + bx + c has discriminant D = b² − 4ac, which is the quantity under the square root sign in the quadratic formula. For real numbers a, b, c, one has:

When D > 0 , P(x) has two distinct real roots 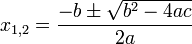$x_{1,2}=\frac{-b \pm \sqrt {b^2-4ac}}{2a}$ , and its graph crosses the x-axis twice.
When D = 0, P(x) has two coincident real roots 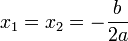$x_1=x_2=-\frac{b}{2a}$ , and its graph is tangent to the x-axis.
When D < 0 , P(x) has no real roots, and its graph lies strictly above or below the x-axis.

Discriminant of a polynomial

The discriminant of the general polynomial

$p(x)=a_n x^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots+a_1 x+a_0$

is, up to a factor, equal to the determinant of the (2n − 1)×(2n − 1) matrix (see Sylvester matrix)

$\left(\begin{matrix} & a_n & a_{n-1} & a_{n-2} & \ldots & a_1 & a_0 & 0 \ldots & \ldots & 0 \\ & 0 & a_n & a_{n-1} & a_{n-2} & \ldots & a_1 & a_0 & 0 \ldots & 0 \\ & \vdots\ &&&&&&&&\vdots\\ & 0 & \ldots\ & 0 & a_n & a_{n-1} & a_{n-2} & \ldots & a_1 & a_0 \\ & na_n & (n-1)a_{n-1} & (n-2)a_{n-2} & \ldots\ & 1a_1 & 0 & \ldots &\ldots & 0 \\ & 0 & na_n & (n-1)a_{n-1} & (n-2)a_{n-2} & \ldots\ & 1a_1 & 0 & \ldots & 0 \\ & \vdots\ &&&&&&&&\vdots\\ & 0 & 0 & \ldots & 0 & na_n & (n-1)a_{n-1} & (n-2)a_{n-2}& \ldots\ & 1a_1 \\ \end{matrix}\right).$

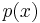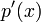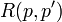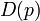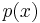The determinant of this matrix is known as the resultant of $p(x)$ and $p'(x)$ , notation $R(p,p')$ . The discriminant $D(p)$ of $p(x)$ is now given by the formula

$D(p)=(-1)^{\frac{1}{2}n(n-1)}\frac{1}{a_n}R(p,p')\,$ .

For example, in the case n = 4, the above determinant is

$\begin{vmatrix} & a_4 & a_3 & a_2 & a_1 & a_0 & 0 & 0 \\ & 0 & a_4 & a_3 & a_2 & a_1 & a_0 & 0 \\ & 0 & 0 & a_4 & a_3 & a_2 & a_1 & a_0 \\ & 4a_4 & 3a_3 & 2a_2 & 1a_1 & 0 & 0 & 0 \\ & 0 & 4a_4 & 3a_3 & 2a_2 & 1a_1 & 0 & 0 \\ & 0 & 0 & 4a_4 & 3a_3 & 2a_2 & 1a_1& 0 \\ & 0 & 0 & 0 & 4a_4 & 3a_3 & 2a_2 & 1a_1 \\ \end{vmatrix}.$

The discriminant of the degree 4 polynomial is then obtained from this determinant upon dividing by 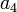$a_4$ .

Equivalently, the discriminant is equal to

$a_n^{2n-2}\prod_{i<j}{(r_i-r_j)^2}$

where r₁, ..., r_n are the complex roots (counting multiplicity) of the polynomial p(x):

$\begin{matrix}p(x)&=&a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0\\ &=&a_n(x-r_1)(x-r_2)\ldots (x-r_n).\end{matrix}$

This second expression makes it clear that, p has a multiple root if and only if the discriminant is zero. (This multiple root can be complex.)

The discriminant can be defined for polynomials over arbitrary fields, in exactly the same fashion as above. The product formula involving the roots r_i remains valid; the roots have to be taken in some splitting field of the polynomial.

Discriminant of a conic section

For a conic section defined by the real polynomial:

$ax^2+ bxy + cy^2 + dx + ey + f= 0\,$

the discriminant is equal to

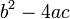$b^2 - 4ac\,$ ,

and determines the shape of the conic section. If the discriminant is less than 0, the equation is of an ellipse or a circle. If the discriminant equals 0, the equation is that of a parabola. If the discriminant is greater than 0, the equation is that of a hyperbola. This formula will not work for degenerate cases (when the polynomial factors).

Discriminant of a quadratic form

There is a substantive generalization to quadratic forms Q over any field K of characteristic ≠ 2. These can be written as a sum of terms

a_iL_i²

where the L_i are linear forms and 1 ≤ i ≤ n where n is the number of variables. Then the discriminant is the product of the a_i, taken in K/K², and is then well defined (i.e., up to squares). A more invariant way to say this is as (the class of) the determinant of a symmetric matrix for Q.

Discriminant of an algebraic number field

Main article: Discriminant of an algebraic number field

Discriminant of a differentiable function

In differential topology, the discriminant of a differentiable function f is the same as the set of critical values of f. The discriminant in this sense is somewhat related to the discriminant of a polynomial; for example, if f(x)=ax²+bx+c is a quadratic (a≠0), then the critical value of f will be 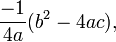$\frac{-1}{4a}(b^2-4ac),$ which is (up to a constant) equal to the discriminant of a quadratic polynomial.