De Moivre's formula
De Moivre's formula, named after Abraham de Moivre, states that for any complex number (and, in particular, for any real number) x and any integer n it holds that
The formula is important because it connects complex numbers (i stands for the imaginary unit) and trigonometry. The expression "cos x + i sin x" is sometimes abbreviated to "cis x".
By expanding the left hand side and then comparing the real and imaginary parts under the assumption that x is real, it is possible to derive useful expressions for cos(nx) and sin(nx) in terms of cos(x) and sin(x). Furthermore, one can use this formula to find explicit expressions for the n-th roots of unity, that is, complex numbers z such that zn = 1.
Contents |
Derivation
Although historically proved earlier, de Moivre's formula can easily be derived from Euler's formula
and the exponential law
Then, by Euler's formula,
Proof by induction
We consider three cases.
For n > 0, we proceed by mathematical induction. When n = 1, the result is clearly true. For our hypothesis, we assume the result is true for some positive integer k. That is, we assume
Now, considering the case n = k + 1:
We deduce that the result is true for n = k + 1 when it is true for n = k. By the principle of mathematical induction it follows that the result is true for all positive integers n≥1.
When n = 0 the formula is true since 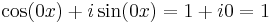 , and (by convention)
, and (by convention) 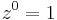 .
.
When n < 0, we consider a positive integer m such that n = −m. So
Hence, the theorem is true for all integer values of n.
Formulas for cosine and sine individually
Being an equality of complex numbers, one necessarily has equality both of the real parts and of the imaginary parts of both members of the equation. If x, and therefore also  and
and  , are real numbers, then the identity of these parts can be written (interchanging sides) as
, are real numbers, then the identity of these parts can be written (interchanging sides) as
These equations are in fact even valid for complex values of x, because both sides are holomorphic functions of x, and two such functions that coincide on the real axis necessarily coincide on the whole complex plane. Here are the concretre instances of these equations for  and
and 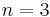 :
:
The right hand side of the formula for 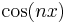 is in fact the value
is in fact the value 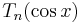 of the Chebyshev polynomial
of the Chebyshev polynomial 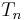 at
at 
Generalization
The formula is actually true in a more general setting than stated above: if z and w are complex numbers, then
is a multivalued function while
is not. Therefore one can state that
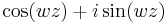 is one value of
is one value of 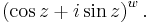

Applications
This formula can be used to find the 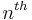 roots of a complex number. If
roots of a complex number. If 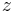 is a complex number, written in polar form as
is a complex number, written in polar form as
then
where 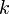 is an integer, to get the
is an integer, to get the 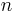 different roots of
different roots of 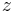 one only needs to consider values of
one only needs to consider values of 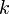 from
from 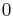 to
to 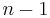 .
.
See also
References
- Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. (p. 74).
External links
- De Moivre's Theorem for Trig Identities by Michael Croucher, Wolfram Demonstrations Project.
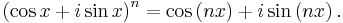
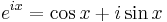
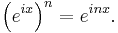
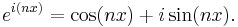
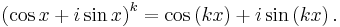
![\begin{alignat}{2}
\left(\cos x+i\sin x\right)^{k+1} & = \left(\cos x+i\sin x\right)^{k} \left(\cos x+i\sin x\right)\\
& = \left[\cos\left(kx\right) + i\sin\left(kx\right)\right] \left(\cos x+i\sin x\right) &&\qquad \mbox{by the induction hypothesis}\\
& = \cos \left(kx\right) \cos x - \sin \left(kx\right) \sin x + i \left[\cos \left(kx\right) \sin x + \sin \left(kx\right) \cos x\right]\\
& = \cos \left[ \left(k+1\right) x \right] + i\sin \left[ \left(k+1\right) x \right] &&\qquad \mbox{by the trigonometric identities}
\end{alignat}](/2009-wikipedia_en_wp1-0.7_2009-05/I/9b74fec2abba905c3154f0c4b8667945.png)
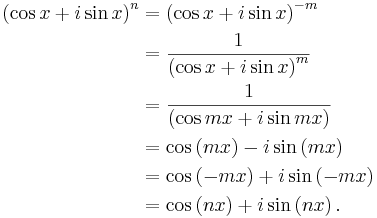
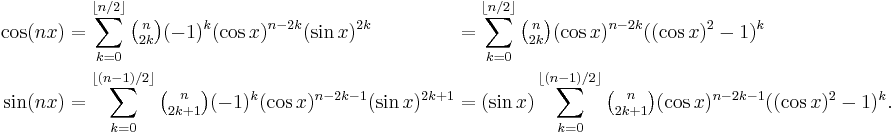
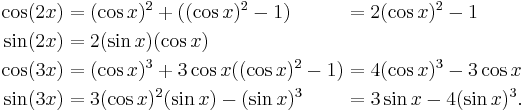
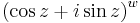

![z^{{}^{\frac{1}{n}}}= \left[ r\left( \cos x+i\sin x \right) \right]^ {{}^{\frac{1}{n}}}= r^{{}^{\frac{1}{n}}} \left[ \cos \left( \frac{x+2k\pi}{n} \right) + i\sin \left( \frac{x+2k\pi}{n} \right) \right]](/2009-wikipedia_en_wp1-0.7_2009-05/I/9f3fc2d5894ed834582447eaa1734d8c.png)