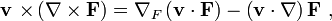Curl (mathematics)
In vector calculus in three-dimensional space, curl (also named: rotor) is a vector operator that shows a vector field's "rotation"; that is, the direction of the axis of rotation and the magnitude of the rotation. It can also be described as the circulation density.
"Rotation" and "circulation" represents variations of the vector function with respect to position, regardless of any variation over time.
A vector field which has zero curl everywhere is called irrotational.
The alternative terminology rotor and alternative notation 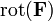 are often used (especially in many European countries) for curl and
are often used (especially in many European countries) for curl and 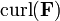 .
.
Contents |
Definition
The curl of a vector field 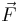 , denoted
, denoted 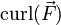 or
or 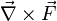 , at a point is defined in terms of its projection onto various lines through the point. If
, at a point is defined in terms of its projection onto various lines through the point. If 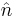 is any unit vector, the projection of the curl of
is any unit vector, the projection of the curl of 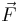 onto
onto 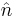 is defined to be the limiting value of a closed line integral in a plane orthogonal to
is defined to be the limiting value of a closed line integral in a plane orthogonal to 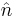 as the path used in the integral becomes infinitesimally close to the point, divided by the area enclosed.
as the path used in the integral becomes infinitesimally close to the point, divided by the area enclosed.
As such, the curl operator maps C1 functions from R3 to R3 to C0 functions from R3 to R3.

Explicitly, curl is defined by:[1]
Here 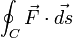 is a line integral around the area in question, and A is the magnitude of the area. If
is a line integral around the area in question, and A is the magnitude of the area. If 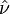 is an outward pointing normal to
is an outward pointing normal to 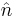 (see caption at right), then the orientation of C is chosen so that a vector
(see caption at right), then the orientation of C is chosen so that a vector 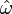 tangent to C is positively oriented if and only if
tangent to C is positively oriented if and only if 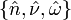 forms a positively oriented basis for R3 (right-hand rule).
forms a positively oriented basis for R3 (right-hand rule).
Intuitive Definition
Suppose the vector field describes the velocity field of a fluid flow (maybe a large tank of water or gas) and a small ball is located within the fluid or gas (the centre of the ball being fixed at a certain point). If the ball has a rough surface it will be made to rotate, by the fluid flowing past it. The rotation axis (oriented according to the right hand rule) points in the direction of the curl of the field at the centre of the ball, and the angular speed of the rotation is half the value of the curl at this point.
Even if all the flow lines are parallel, the ball can start spinning if the fluid moves past it faster on one side than the other.
A small paddle wheel whose centre is located at the point in question will rotate fastest when its axis is aligned with the curl vector. In this position, it will rotate counterclockwise according to the right-hand rule. Its angular speed will be half the length of the curl vector.
Usage
In practice, the above definition is rarely used because in virtually all cases, the curl operator can be applied using some set of curvilinear coordinates, for which simpler representations have been derived.
Although the usage of 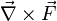 is strictly an abuse of notation, it is still useful as a mnemonic in Cartesian coordinates if we take
is strictly an abuse of notation, it is still useful as a mnemonic in Cartesian coordinates if we take  as a vector differential operator del or nabla. Such notation involving operators is common in physics and algebra.
as a vector differential operator del or nabla. Such notation involving operators is common in physics and algebra.
Expanded in Cartesian coordinates (see: Del in cylindrical and spherical coordinates for spherical and cylindrical coordinate representations), 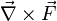 is, for F composed of [Fx, Fy, Fz]:
is, for F composed of [Fx, Fy, Fz]:
where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively. This expands as follows:
Although expressed in terms of coordinates, the result is invariant under proper rotations of the coordinate axes but the result inverts under reflection.
In Einstein notation, with the Levi-Civita symbol it is written as:
or as:
for unit vectors: , k=1,2,3 corresponding to
, k=1,2,3 corresponding to 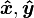 , and
, and 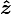 respectively.
respectively.
Using the exterior derivative, the curl can be expressed as:
Here 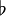 and
and 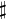 are the musical isomorphisms, and
are the musical isomorphisms, and 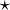 is the Hodge dual. This formula shows how to calculate the curl of F in any coordinate system, and how to extend the curl to any oriented three dimensional Riemmannian manifold. Since this depends on a choice of orientation, curl is a chiral operation. In other words, if the orientation is reversed, then the direction of the curl is also reversed.
is the Hodge dual. This formula shows how to calculate the curl of F in any coordinate system, and how to extend the curl to any oriented three dimensional Riemmannian manifold. Since this depends on a choice of orientation, curl is a chiral operation. In other words, if the orientation is reversed, then the direction of the curl is also reversed.
Examples
A simple vector field
Take the vector field, which depends on x and y linearly:
Its plot looks like this:
Simply by visual inspection, we can see that the field is rotating. If we stick a paddle wheel anywhere, we see immediately its tendency to rotate clockwise. Using the right-hand rule, we expect the curl to be into the page. If we are to keep a right-handed coordinate system, into the page will be in the negative z direction. The lack of x and y directions is analogous to the cross product operation.
If we do the math and find the curl:
Which is indeed in the negative z direction, as expected. In this case, the curl is actually a constant, irrespective of position. The "amount" of rotation in the above vector field is the same at any point (x,y). Plotting the curl of F isn't very interesting:
A more involved example
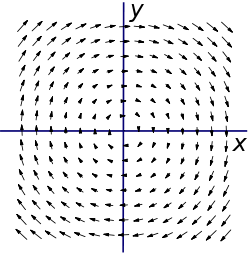
Suppose we now consider a slightly more complicated vector field:
Its plot:
We might not see any rotation initially, but if we closely look at the right, we see a larger field at, say, x=4 than at x=3. Intuitively, if we placed a small paddle wheel there, the larger "current" on its right side would cause the paddlewheel to rotate clockwise, which corresponds to a curl in the negative z direction. By contrast, if we look at a point on the left and placed a small paddle wheel there, the larger "current" on its left side would cause the paddlewheel to rotate counterclockwise, which corresponds to a curl in the positive z direction. Let's check out our guess by doing the math:
Indeed the curl is in the positive z direction for negative x and in the negative z direction for positive x, as expected. Since this curl is not the same at every point, its plot is a bit more interesting:
We note that the plot of this curl has no dependence on y or z (as it shouldn't) and is in the negative z direction for positive x and in the positive z direction for negative x.
Three common identities
Consider the example ∇ × [ v × F ]. Using Cartesian coordinates, it can be shown that
In the case where the vector field v and ∇ are interchanged:
which introduces the Feynman subscript notation ∇F, which means the subscripted gradient operates on only the factor F.
Another example is ∇ × [ ∇ × F ]. Using Cartesian coordinates, it can be shown that:
which can be construed as a special case of the first example with the substitution v → ∇.
Descriptive examples
- In a vector field that describes the linear velocities of each individual part of a rotating disk, the curl will have a constant value on all parts of the disk.
- If velocities of cars on a freeway were described with a vector field, and the lanes had different speed limits, the curl on the borders between lanes would be non-zero.
- Faraday's law of induction, one of Maxwell's equations, can be expressed very simply using curl. It states that the curl of an electric field is equal to the opposite of the time rate of change of the magnetic field.
See also
- Del
- Gradient
- Divergence
- Nabla in cylindrical and spherical coordinates
- Vorticity
- Cross product
- Helmholtz decomposition
Notes
References
- Theresa M. Korn; Korn, Granino Arthur. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York: Dover Publications. pp. 157–160. ISBN 0-486-41147-8.
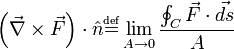

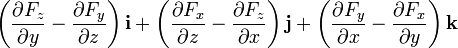
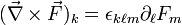
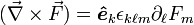
![\vec{\nabla} \times \vec{F} = \left[ \star \left( {\mathbf d} F^\flat \right) \right]^\sharp](/2009-wikipedia_en_wp1-0.7_2009-05/I/ba9757a55e4bdcef5320326fc2958155.png)
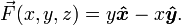
![\vec{\nabla} \times \vec{F} =0\boldsymbol{\hat{x}}+0\boldsymbol{\hat{y}}+ [{\frac{\partial}{\partial x}}(-x) -{\frac{\partial}{\partial y}} y]\boldsymbol{\hat{z}}=-2\boldsymbol{\hat{z}}](/2009-wikipedia_en_wp1-0.7_2009-05/I/308266a9235d72638006c5b51bd0faea.png)
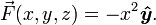
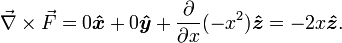
![\mathbf{ \nabla \times} \left( \mathbf{v \times F} \right) = \left[ \left( \mathbf{ \nabla \cdot F } \right) + \mathbf{F \cdot \nabla} \right] \mathbf{v}- \left[ \left( \mathbf{ \nabla \cdot v } \right) + \mathbf{v \cdot \nabla} \right] \mathbf{F} \ .](/2009-wikipedia_en_wp1-0.7_2009-05/I/2628b53319924465c2409f2d3b024ef5.png)