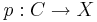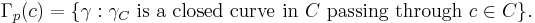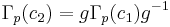Covering space
In mathematics, a covering space is a topological space C which "covers" another space X by a surjective local homeomorphism p : C → X called a covering map. The precise definition is given below. Covering spaces are studied in algebraic topology, but they have important applications in many other branches of mathematics including differential topology, the theory of topological groups, and the theory of Riemann surfaces.
The theory of covering spaces is deeply intertwined with the study of homotopy groups. It is nearly impossible to take up a study of one without encountering the other.
Contents |
Formal definition
Let X be a topological space. A covering space of X is a space C together with a continuous surjective map
such that for every x ∈ X there exists an open neighborhood U of x such that p−1(U) (the inverse image of U under p) is a disjoint union of open sets in C each of which is mapped homeomorphically onto U by p.
The map p is called the covering map and the space X is often called the base of the covering. For any point x in the base the inverse image of x in C is a discrete space called the fiber over x.
The special open neighborhoods U of x given in the definition are called evenly-covered neighborhoods. The evenly-covered neighborhoods form an open cover of the space X. The homeomorphic copies in C of an evenly-covered neighborhood U are called the sheets over U. One generally pictures C as "hovering above" X, with p mapping "downwards", the sheets over U being horizontally stacked above each other and above U, and the fiber over x consisting of those points of C that lie "vertically above" x.
Warning: Many authors impose some connectivity conditions on the spaces X and C in the definition of a covering map. In particular, many authors require both spaces to be path-connected and locally path-connected . When studying results about covering spaces, one should always be careful to check the connectivity assumptions the author is making. Also some authors do not require covering maps to be surjective. However, if X is connected and C is nonempty then surjectivity of the covering map actually follows from the other axioms.
Examples
Consider the unit circle S1 in R2. Then the map p : R → S1 with
- p(t) = (cos(t),sin(t))
is a cover where each point of S1 is covered infinitely often.
Consider the complex plane with the origin removed, denoted by C×, and pick a non-zero integer n. Then p : C× → C× given by
- p(z) = zn
is a cover. Here every fiber has n elements.
A further example, originating from physics (see quantum mechanics), is the special orthogonal group SO(3) of rotations of  , which has the "double" covering group SU(2) of unitary rotations of
, which has the "double" covering group SU(2) of unitary rotations of 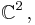 (in quantum mechanics acting as the group of spinor rotations). Both groups have identical Lie algebras, but only SU(2) is simply connected.
(in quantum mechanics acting as the group of spinor rotations). Both groups have identical Lie algebras, but only SU(2) is simply connected.
Properties
Common local properties: Every cover p : C → X is a local homeomorphism (i.e. to every 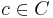 there exists an open set A in C containing c and an open set B in X such that the restriction of p to A yields a homeomorphism between A and B). This implies that C and X share all local properties. If X is simply connected and C is connected, then this holds globally as well, and the covering p is a homeomorphism.
there exists an open set A in C containing c and an open set B in X such that the restriction of p to A yields a homeomorphism between A and B). This implies that C and X share all local properties. If X is simply connected and C is connected, then this holds globally as well, and the covering p is a homeomorphism.
Equivalence of fibers in the category top: For every x in X, the fiber over x is a discrete subset of C. On every connected component of X, the fibers are homeomorphic. If every fiber has n elements, we speak of an n-fold covering (for the case n = 1, the covering is trivial; when n = 2, the covering is a double cover; when n = 3, the covering is a triple cover and so on).
The lifting property: If p : C → X is a cover and γ is a path in X (i.e. a continuous map from the unit interval [0,1] into X) and 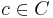 is a point "lying over" γ(0) (i.e. p(c) = γ(0)), then there exists a unique path ρ in C lying over γ (i.e. p o ρ = γ) and with ρ(0) = c. The curve ρ is called the lift of γ. If x and y are two points in X connected by a path, then that path furnishes a bijection between the fiber over x and the fiber over y via the lifting property.
is a point "lying over" γ(0) (i.e. p(c) = γ(0)), then there exists a unique path ρ in C lying over γ (i.e. p o ρ = γ) and with ρ(0) = c. The curve ρ is called the lift of γ. If x and y are two points in X connected by a path, then that path furnishes a bijection between the fiber over x and the fiber over y via the lifting property.
Equivalence: Let 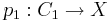 and
and 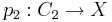 be two coverings. One then says that the two coverings
be two coverings. One then says that the two coverings 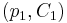 and
and  are equivalent if there exists a homeomorphism
are equivalent if there exists a homeomorphism 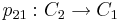 and
and 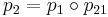 . Equivalence classes of coverings correspond to conjugacy classes, as discussed below. If
. Equivalence classes of coverings correspond to conjugacy classes, as discussed below. If 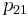 is a covering rather than a homeomorphism, then one says that
is a covering rather than a homeomorphism, then one says that  dominates
dominates 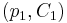 (given that
(given that 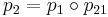 ).
).
Universal covers
A connected covering space is a universal cover if it is simply connected. The name universal cover comes from the following important property: if the mapping q : D → X is a universal cover of the space X and the mapping p : C → X is any cover of the space X where the covering space C is connected, then there exists a covering map f : D → C such that p ◦ f = q. This can be phrased as
The universal cover of the space X covers all connected covers of the space X.
The map f is unique in the following sense: if we fix a point x in the space X and a point d in the space D with q(d) = x and a point c in the space C with p(c) = x, then there exists a unique covering map f : D → C such that p ◦ f = q and f(d) = c.
If the space X has a universal cover then that universal cover is essentially unique: if the mappings q1 : D1 → X and q2 : D2 → X are two universal covers of the space X then there exists a homeomorphism f : D1 → D2 such that q2 ◦ f = q1.
The space X has a universal cover if it is connected, locally path-connected and semi-locally simply connected. The universal cover of the space X can be constructed as a certain space of paths in the space X.
The example R → S1 given above is a universal cover. The map S3 → SO(3) from unit quaternions to rotations of 3D space described in quaternions and spatial rotation is also a universal cover.
If the space X carries some additional structure, then its universal cover normally inherits that structure:
- if the space X is a manifold, then so is its universal cover D
- if the space X is a Riemann surface, then so is its universal cover D, and p is a holomorphic map
- if the space X is a Lorentzian manifold, then so is its universal cover. Furthermore, suppose the subset p−1(U) is a disjoint union of open sets each of which is diffeomorphic with U by the mapping p. If the space X contains a closed timelike curve, then the space X is timelike multiply connected (no CTC can be timelike homotopic to a point, as that point would not be causally well-behaved), its universal (diffeomorphic) cover is timelike simply connected (it does not contain a CTC).
- if X is a Lie group (as in the two examples above), then so is its universal cover D, and the mapping p is a homomorphism of Lie groups. In this case the universal cover is also called the universal covering group. This has particular application to representation theory and quantum mechanics, since ordinary representations of the universal covering group (D) are projective representations of the original (classical) group (X).
The universal cover first arose in the theory of analytic functions as the natural domain of an analytic continuation.
Deck transformation group, regular covers
A deck transformation or automorphism of a cover p : C → X is a homeomorphism f : C → C such that p o f = p. The set of all deck transformations of p forms a group under composition, the deck transformation group Aut(p). Deck transformations are also called covering transformations. Every deck transformation permutes the elements of each fiber. This defines a group action of the deck transformation group on each fiber. Note that by the unique lifting property, if f is not the identity and C is path connected, then f has no fixed points.
Now suppose p : C → X is a covering map and C (and therefore also X) is connected and locally path connected. The action of Aut(p) on each fiber is free. If this action is transitive on some fiber, then it is transitive on all fibers, and we call the cover regular. Every such regular cover is a principal G-bundle, where G = Aut(p) is considered as a discrete topological group.
Every universal cover p : D → X is regular, with deck transformation group being isomorphic to the fundamental group 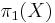 .
.
The example p : C× → C× with p(z) = zn from above is a regular cover. The deck transformations are multiplications with n-th roots of unity and the deck transformation group is therefore isomorphic to the cyclic group Cn.
Another example: 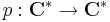 with
with 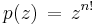 from above is regular. Here one has a hierarchy of deck transformation groups. In fact Cx! is a subgroup of Cy!, for
from above is regular. Here one has a hierarchy of deck transformation groups. In fact Cx! is a subgroup of Cy!, for 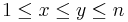 .
.
Monodromy action
Again suppose p : C → X is a covering map and C (and therefore also X) is connected and locally path connected. If x in X and c belongs to the fiber over x (i.e. p(c) = x), and γ:[0,1]→X is a path with γ(0)=γ(1)=x, then this path lifts to a unique path in C with starting point c. The end point of this lifted path need not be c, but it must lie in the fiber over x. It turns out that this end point only depends on the class of γ in the fundamental group  , and in this fashion we obtain a right group action of
, and in this fashion we obtain a right group action of  on the fiber over x. This is known as the monodromy action.
on the fiber over x. This is known as the monodromy action.
So there are two actions on the fiber over x: Aut(p) acts on the left and  acts on the right. These two actions are compatible in the following sense:
acts on the right. These two actions are compatible in the following sense:
- f.(c.γ) = (f.c).γ
for all f in Aut(p), c in p -1(x) and γ in  .
.
If p is a universal cover, then the monodromy action is regular; if we identify Aut(p) with the opposite group of π(X,x), then the monodromy action coincides with the action of Aut(p) on the fiber over x.
More on the group structure
The deck transformation group and the monodromy action can be understood to relate the normal subgroups of the fundamental group 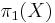 of X and the fundamental group
of X and the fundamental group 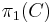 of the cover. Furthermore, these equate the conjugacy classes of subgroups of
of the cover. Furthermore, these equate the conjugacy classes of subgroups of 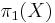 and equivalence classes of coverings. As a result, one can conclude that X=C/Aut(p), that is, the manifold X is given as the quotient of the covering manifold under the action of the deck transformation group. These inter-relationships are explored below.
and equivalence classes of coverings. As a result, one can conclude that X=C/Aut(p), that is, the manifold X is given as the quotient of the covering manifold under the action of the deck transformation group. These inter-relationships are explored below.
Let γ be a curve in X. Denote by 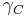 the lift of γ to C. Consider the set
the lift of γ to C. Consider the set
Note that 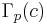 is a group, and that it is a subgroup of
is a group, and that it is a subgroup of 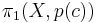 . Note also that it depends on c, and that different values of c in the same fiber yield different subgroups. Each such subgroups is conjugate to another by the monodromy action. To see this, pick two points
. Note also that it depends on c, and that different values of c in the same fiber yield different subgroups. Each such subgroups is conjugate to another by the monodromy action. To see this, pick two points 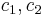 in the same fiber:
in the same fiber: 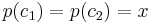 and let g be a curve in C connecting
and let g be a curve in C connecting 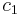 to
to  . Then p(g) is a closed curve in X. If
. Then p(g) is a closed curve in X. If 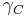 is a closed curve in C passing through
is a closed curve in C passing through 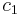 , then
, then 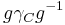 is a closed curve in C passing through
is a closed curve in C passing through  . Thus, we have shown
. Thus, we have shown
and so we have the result that 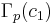 and
and 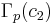 are conjugate subgroups of
are conjugate subgroups of  . All of the conjugate subgroups may be obtained in this way.
. All of the conjugate subgroups may be obtained in this way.
It should be clear that two equivalent coverings lead to the same conjugacy class of subgroups of  ; there is a bijective correspondence between equivalence classes of coverings and conjugacy classes of subgroups of
; there is a bijective correspondence between equivalence classes of coverings and conjugacy classes of subgroups of 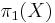 .
.
Note that this implies that the fundamental group 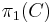 is isomorphic to
is isomorphic to 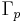 . Let
. Let 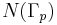 be the normalizer of
be the normalizer of 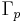 in
in 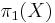 . The deck transformation group Aut(p) is isomorphic to
. The deck transformation group Aut(p) is isomorphic to 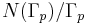 . If p is a universal covering, then
. If p is a universal covering, then 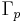 is the trivial group, and Aut(p) is isomorphic to
is the trivial group, and Aut(p) is isomorphic to 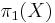 .
.
As a corollary, let us reverse this argument. Let Γ be a normal subgroup of  . By the above arguments, this defines a (regular) covering
. By the above arguments, this defines a (regular) covering 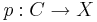 . Let
. Let 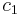 in C be in the fiber of x. Then for every other
in C be in the fiber of x. Then for every other  in the fiber of x, there is precisely one deck transformation that takes
in the fiber of x, there is precisely one deck transformation that takes 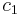 to
to  . This deck transformation corresponds to a curve g in C connecting
. This deck transformation corresponds to a curve g in C connecting 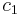 to
to  .
.
Note that Aut(p) operates properly discontinuously on C, and so we have that X=C/Aut(p), that is, X is the manifold given by the quotient of the covering manifold by the deck transformation group.
Relations with groupoids
One of the ways of expressing the algebraic content of the theory of covering spaces is using groupoids and the fundamental groupoid. The latter functor gives an equivalence of categories between the category of covering spaces of a reasonably nice space X and the category of groupoid covering morphisms of 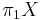 . The latter category is also equivalent to the category of actions of that groupoid on sets. Proofs of these facts are given in the book `Topology and Groupoids' referenced below.
. The latter category is also equivalent to the category of actions of that groupoid on sets. Proofs of these facts are given in the book `Topology and Groupoids' referenced below.
Generalizations
As a homotopy theory, the notion of covering spaces works well when the deck transformation group is discrete, or, equivalently, when the space is locally path-connected. However, when the deck transformation group is a topological group whose topology is not discrete, difficulties arise. Some progress has been made for more complex spaces, such as the Hawaiian earring; see the references there for further information.
See also
- Covering group
- Galois connection
References
- Farkas, Hershel M.; Irwin Kra (1980). Riemann Surfaces (2nd ed. ed.). New York: Springer. ISBN 0-387-90465-4. See chapter 1 for a simple review.
- Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0. http://www.math.cornell.edu/~hatcher/AT/ATpage.html.
- Jost, Jurgen (2002). Compact Riemann Surfaces. New York: Springer. ISBN 3-540-43299-X. See section 1.3
- Massey, William (1991). A Basic Course in Algebraic Topology. New York: Springer. ISBN 0-387-97430-X. See chapter 5.
- Brown, Ronald (2006). Topology and Groupoids. Charleston, S. Carolina: Booksurge LLC. ISBN 1-4196-2722-8. http://www.bangor.ac.uk/r.brown/topgpds.html. See chapter 10.
- Categories and groupoids, P.J. Higgins, downloadable reprint of van Nostrand Notes in Mathematics, 1971, which deal with applications of groupoids in group theory and topology.