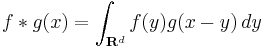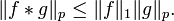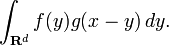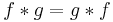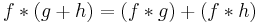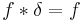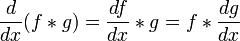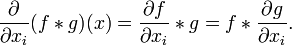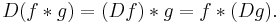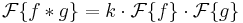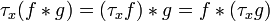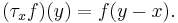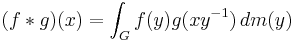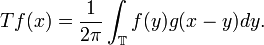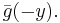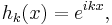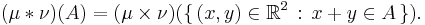Convolution
1.Express each function in terms of a dummy variable
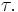
2.Transpose one of the functions:
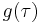 →
→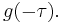
3.Add a time-offset, t, which allows
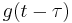 to slide along the
to slide along the  -axis.
-axis.4.Start t at -∞ and slide it all the way to +∞. Wherever the two functions intersect, find the integral of their product. In other words, compute a sliding, weighted-average of function
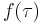 , where the weighting function is
, where the weighting function is 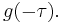
The resulting waveform (not shown here) is the convolution of functions f and g. If f(t) is a unit impulse, the result of this process is simply g(t), which is therefore called the impulse response.
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation. It has applications that include statistics, computer vision, image and signal processing, electrical engineering, and differential equations.
The convolution can be defined for functions on groups other than Euclidean space. In particular, the circular convolution can be defined for periodic functions (that is, functions on the circle), and the discrete convolution can be defined for functions on the set of integers. These generalizations of the convolution have applications in the field of numerical analysis and numerical linear algebra, and in the design and implementation of finite impulse response filters in signal processing.
Contents |
Definition
The convolution of  and
and 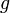 is written
is written 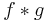 . It is defined as the integral of the product of the two functions after one is reversed and shifted. As such, it is a particular kind of integral transform:
. It is defined as the integral of the product of the two functions after one is reversed and shifted. As such, it is a particular kind of integral transform:
While the symbol 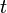 is used above, it need not represent the time domain. But in that context, the convolution formula can be described as a weighted average of the function
is used above, it need not represent the time domain. But in that context, the convolution formula can be described as a weighted average of the function 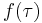 at the moment
at the moment 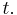 The weighting function is
The weighting function is 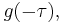 simply shifted by amount
simply shifted by amount 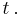 As
As 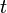 changes, the weighting function emphasizes different parts of the input function.
changes, the weighting function emphasizes different parts of the input function.
More generally, if f and g are complex-valued functions on Rd, then their convolution may be defined as the integral
Circular convolution
When a function gT is periodic, with period T (and f is not), then ƒ*gT is also periodic and identical to:
where to is an arbitrary choice. The summation is called a periodic extension of the function ƒ.
If gT is a periodic extension of another function, g, then ƒ*gT is known as a circular, cyclic, or periodic convolution of f and g.
Discrete convolution
For complex-valued functions ƒ, g defined on the set of integers, the discrete convolution of ƒ and g is given by:
When multiplying two polynomials, the coefficients of the product are given by the convolution of the original coefficient sequences, extended with zeros where necessary to avoid undefined terms; this is known as the Cauchy product of the coefficients of the two polynomials.
Circular discrete convolution
When a function gN is periodic, with period N (and f is not), then ƒ*gN is also periodic and identical to:
The summation on k is called a periodic extension of the function ƒ.
If gN is a periodic extension of another function, g, then ƒ*gN is known as a circular, cyclic, or periodic convolution of f and g.
When the non-zero durations of both f and g are limited to the interval [0, N-1], ƒ*gN reduces to these common forms:
-
![(f * g_N)[n] = \sum_{m=0}^{N-1} f[m]\ g_N[n-m]\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/e76d14d6835f663dfe74a4889acda96e.png)
(
The notation 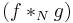 for cyclic convolution denotes convolution over the cyclic group of integers modulo N.
for cyclic convolution denotes convolution over the cyclic group of integers modulo N.
Fast convolution algorithms
In many situations, discrete convolutions can be converted to circular convolutions so that fast transforms with a convolution property can be used to implement the computation. For example, convolution of digit sequences is the kernel operation in multiplication of multi-digit numbers, which can therefore be efficiently implemented with transform techniques (Knuth 1997, §4.3.3.C; von zur Gathen & Gerhard 2003, §8.2).
Eq.1 requires N arithmetic operations per output value and N2 operations for N outputs. That can be significantly reduced with any of several fast algorithms. Digital signal processing and other applications typically use fast convolution algorithms to reduce the cost of the convolution to O(N log N) complexity.
The most common fast convolution algorithms use fast Fourier transform (FFT) algorithms via the circular convolution theorem. Specifically, the circular convolution of two finite-length sequences is found by taking an FFT of each sequence, multiplying pointwise, and then performing an inverse FFT. Convolutions of the type defined above are then efficiently implemented using that technique in conjunction with zero-extension and/or discarding portions of the output. Other fast convolution algorithms, such as the Schönhage-Strassen algorithm, use fast Fourier transforms in other rings.
Domain of definition
The convolution of two complex-valued functions on Rd
is well-defined only if ƒ and g decay sufficiently rapidly at infinity in order for the integral to exist. Conditions for the existence of the convolution may be tricky, since a blow-up in g at infinity can be easily offset by sufficiently rapid decay in ƒ. The question of existence thus may involve different conditions on ƒ and g.
Compactly supported functions
If ƒ and g are compactly supported continuous functions, then their convolution exists, and is also compactly supported and continuous (Hörmander). More generally, if either function (say ƒ) is compactly supported and the other is locally integrable, then the convolution ƒ*g is well-defined and continuous.
Integrable functions
The convolution of ƒ and g exists if ƒ and g are both Lebesgue integrable functions (in L1(Rd)), and ƒ*g is also integrable (Stein & Weiss 1971, Theorem 1.3). This is a consequence of Tonelli's theorem. Likewise, if ƒ∈L1(Rd) and g ∈ Lp(Rd) where 1 ≤ p ≤ ∞, then ƒ*g ∈ Lp(Rd) and
Functions of rapid decay
In addition to compactly supported functions and integrable functions, functions that have sufficiently rapid decay at infinity can also be convolved. An important feature of the convolution is that if ƒ and g both decay rapidly, then ƒ*g also decays rapidly. In particular, if ƒ and g are rapidly decreasing functions, then so is the convolution ƒ*g. Combined with the fact that convolution commutes with differentiation (see Properties), it follows that the class of Schwartz functions is closed under convolution.
Distributions
Under some circumstances, it is possible to define the convolution of a function with a distribution, or of two distributions. If ƒ is a compactly supported function and g is a distribution, then ƒ*g is a smooth function defined by a distributional formula analogous to
More generally, it is possible to extend the definition of the convolution in a unique way so that the associative law
remains valid in the case where ƒ is a distribution, and g a compactly supported distribution (Hörmander 1983, §4.2).
Properties
Algebraic properties
- See also: Convolution algebra
The convolution defines a product on the linear space of integrable functions. This product satisfies the following algebraic properties, which formally mean that the space of integrable functions with the product given by convolution is a commutative algebra without identity (Strichartz 1994, §3.3). Other linear spaces of functions, such as the space of continuous functions of compact support, are closed under the convolution, and so also form commutative algebras.
- Associativity with scalar multiplication
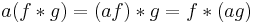
for any real (or complex) number 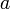 .
.
No algebra of functions possesses an identity for the convolution. The lack of identity is typically not a major inconvenience, since most collections of functions on which the convolution is performed can be convolved with a delta distribution or, at the very least (as is the case of L1) admit approximations to the identity.
The linear space of compactly supported distributions does, however, admit an identity under the convolution. Specifically,
where δ is the delta distribution.
Differentiation
In the one variable case,
where d/dx is the derivative. More generally, in the case of functions of several variables, an analogous formula holds with the partial derivative:
A particular consequence of this is that the convolution can be viewed as a "smoothing" operation: the convolution of ƒ and g is differentiable as many times as ƒ and g are together.
In the discrete case, the difference operator Dƒ(n) = ƒ(n+1) − ƒ(n) satisfies an analogous relationship:
Convolution theorem
The convolution theorem states that
where 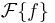 denotes the Fourier transform of
denotes the Fourier transform of 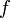 , and
, and 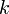 is a constant that depends on the specific normalization of the Fourier transform (see Fourier transform#Some Fourier transform properties). Versions of this theorem also hold for the Laplace transform, two-sided Laplace transform, Z-transform and Mellin transform.
is a constant that depends on the specific normalization of the Fourier transform (see Fourier transform#Some Fourier transform properties). Versions of this theorem also hold for the Laplace transform, two-sided Laplace transform, Z-transform and Mellin transform.
See also the less trivial Titchmarsh convolution theorem.
Translation invariance
The convolution commutes with translations, meaning that
where τxƒ is the translation of the function ƒ by x defined by
Furthermore, under certain conditions, convolution is the most general translation invariant operation. Roughly speaking, the following holds
- Suppose that S is a linear operator acting on functions which commutes with translations: S(τxƒ) = τx(Sƒ) for all x. Then S is given as convolution with a function (or distribution) gS; that is Sƒ = gS*ƒ.
Thus any translation invariant operation can be represented as a convolution. Convolutions play an important role in the study of time-invariant systems, and especially LTI system theory. The representing function gS is the impulse response of the transformation S.
Convolution inverse
Many functions have an inverse element, f(-1), which satisfies the relationship:
These functions form an abelian group, with the group operation being convolution.
Convolutions on groups
If G is a suitable group endowed with a measure m (for instance, a locally compact Hausdorff topological group with the Haar measure) and if f and g are real or complex valued m-integrable functions on G, then we can define their convolution by
The circle group T with the Lebesgue measure is an immediate example. For a fixed g in L1(T), we have the following familiar operator acting on the Hilbert space L2(T):
The operator T is compact. A direct calculation shows that its adjoint T* is convolution with
By the commutativity property cited above, T is normal, i.e. T*T = TT*. Also, T commutes with the translation operators. Consider the family S of operators consisting of all such convolutions and the translation operators. S is a commuting family of normal operators. According to spectral theory, there exists an orthonormal basis {hk} that simultaneously diagonalizes S. This characterizes convolutions on the circle. Specifically, we have
which are precisely the characters of T. Each convolution is a compact multiplication operator in this basis. This can be viewed as a version of the convolution theorem discussed above.
The above example may convince one that convolutions arise naturally in the context of harmonic analysis on groups. For more general groups, it is also possible to give, for instance, a Convolution Theorem, however it is much more difficult to phrase and requires representation theory for these types of groups and the Peter-Weyl theorem. It is very difficult to do these calculations without more structure, and Lie groups turn out to be the setting in which these things are done.
Convolution of measures
If μ and ν are measures on the family of Borel subsets of the real line, then the convolution μ * ν is defined by
In case μ and ν are absolutely continuous with respect to Lebesgue measure, so that each has a density function, then the convolution μ * ν is also absolutely continuous, and its density function is just the convolution of the two separate density functions.
If μ and ν are probability measures, then the convolution μ * ν is the probability distribution of the sum X + Y of two independent random variables X and Y whose respective distributions are μ and ν.
Applications
Convolution and related operations are found in many applications of engineering and mathematics.
- In electrical engineering, the convolution of one function (the input) with a brief but strong impulse (see impulse response) gives the output of a linear time-invariant system. At any given moment, the output is an accumulated effect of all the prior values of the input function, with the most recent values typically having the most influence (expressed as a multiplicative factor). The impulse response function provides that factor as a function of the elapsed time since each input value occurred.
- In statistics, as noted above, a weighted moving average is a convolution.
- In probability theory, the probability distribution of the sum of two independent random variables is the convolution of their individual distributions.
- In optics, many kinds of "blur" are described by convolutions. A shadow (e.g. the shadow on the table when you hold your hand between the table and a light source) is the convolution of the shape of the light source that is casting the shadow and the object whose shadow is being cast. An out-of-focus photograph is the convolution of the sharp image with the shape of the iris diaphragm. The photographic term for this is bokeh.
- Similarly, in digital image processing, convolutional filtering plays an important role in many important algorithms in edge detection and related processes.
- In linear acoustics, an echo is the convolution of the original sound with a function representing the various objects that are reflecting it.
- In artificial reverberation (digital signal processing, pro audio), convolution is used to map the impulse response of a real room on a digital audio signal (see previous and next point for additional information).
- In time-resolved fluorescence spectroscopy, the excitation signal can be treated as a chain of delta pulses, and the measured fluorescence is a sum of exponential decays from each delta pulse.
- In physics, wherever there is a linear system with a "superposition principle", a convolution operation makes an appearance.
- This is the fundamental problem term in the Navier–Stokes equations relating to the Clay Mathematics Millennium Problem and the associated million dollar prize.
- In digital signal processing, frequency filtering can be simplified by convolving two functions (data with a filter) in the time domain, which is analogous to multiplying the data with a filter in the frequency domain.
See also
- LTI system theory#Impulse response and convolution
- Toeplitz matrix (convolutions can be considered a Toeplitz matrix operation where each row is a shifted copy of the convolution kernel)
- Circulant matrix
- Cross-correlation
- Deconvolution
- Dirichlet convolution
- Titchmarsh convolution theorem
- Convolution power
- Analog signal processing
- List of convolutions of probability distributions
- Jan Mikusinski
References
- Bracewell, R. (1986), The Fourier Transform and Its Applications (2nd ed ed.), McGraw-Hill.
- Hörmander, L. (1983), The analysis of linear partial differential operators I, Grundl. Math. Wissenschaft., 256, Springer, MR0717035, ISBN 3-540-12104-8.
- Knuth, Donald (1997), Seminumerical Algorithms (3rd. ed.), Reading, Massachusetts: Addison-Wesley, ISBN 0-201-89684-2.
- Sobolev, V.I. (2001), "Convolution of functions", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, ISBN 0-691-08078-X.
- Strichartz, R. (1994), A Guide to Distribution Theory and Fourier Transforms, CRC Press, ISBN 0849382734.
- Titchmarsh, E (1948), Introduction to the theory of Fourier integrals (2nd ed.) (published 1986), ISBN 978-0828403245.
- Treves, François (1967), Topological Vector Spaces, Distributions and Kernels, Academic Press.
- von zur Gathen, J.; Gerhard, J. (2003), Modern Computer Algebra, Cambridge University Press, ISBN 0-521-82646-2.
External links
- http://www.nitte.ac.in/downloads/Conv-LTI.pdf
- Convolution, on The Data Analysis BriefBook
- http://www.jhu.edu/~signals/convolve/index.html Visual convolution Java Applet.
- http://www.jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet for Discrete Time functions.
- Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lecture 7 is on 2-D convolution., by Alan Peters.
- Convolution Kernel Mask Operation Interactive tutorial
- Convolution at MathWorld
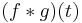
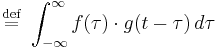
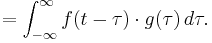 (
(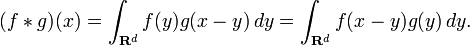
![(f * g_T)(t) \equiv \int_{t_0}^{t_0+T} \left[\sum_{k=-\infty}^{\infty} f(\tau + kT)\right] g_T(t - \tau)\ d\tau,\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/965d2b9f597857897e762ef92fbb810c.png)
![(f * g)[n]\ \stackrel{\mathrm{def}}{=}\ \sum_{m=-\infty}^{\infty} f[m]\cdot g[n - m]\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/43d1a879cfbf7775af5bdeb7d1865de0.png)
![= \sum_{m=-\infty}^{\infty} f[n-m]\cdot g[m].\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/a402887521888aa6e09eaa4721cc2b3c.png) (
(![(f * g_N)[n] \equiv \sum_{m=0}^{N-1} \left(\sum_{k=-\infty}^{\infty} {f}[m+kN] \right) g_N[n-m].\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/a4016b01a160f5c1e757282ad6494aa4.png)
![= \sum_{m=0}^n f[m]\ g[n-m] + \sum_{m=n+1}^{N-1} f[m]\ g[N+n-m]\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/289c42f534ead7fee418aab4da700cc7.png)
![= \sum_{m=0}^{N-1} f[m]\ g[(n-m)_{\mod{N}}]\quad \stackrel{\mathrm{def}}{=}\quad (f *_N g)[n].\,](/2009-wikipedia_en_wp1-0.7_2009-05/I/fced7004a512fadd2bd585897d478d59.png)