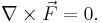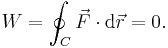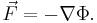Conservative force

A conservative force is defined as a force with the following property: when an object moves from one location to another, the force changes the potential energy of the object by an amount that does not depend on the path taken.

Informal definition

Informally, a conservative force can be thought of as a force that conserves mechanical energy. Suppose a particle starts at point A, and there is a constant force F acting on it. Then the particle is moved around by other forces, and eventually ends up at A again. Though the particle may still be moving, at that instant when it passes point A again, it has traveled a closed path. If the net work done by F at this point is 0, then F passes the closed path test. Any force that passes the closed path test is classified as a conservative force.

The gravitational force, spring force, magnetic force (according to some definitions, see below) and electric force (at least in a time-independent magnetic field, see Faraday's law of induction for details) are examples of conservative forces, while friction and air drag are classical examples of non-conservative forces (the energy is transferred to the air as heat and cannot be retrieved)

Path independence

The work done by the gravitational force on an object depends only on its change in height because the gravitational force is conservative.

A direct consequence of the closed path test is that the work done by a conservative force on a particle moving between any two points does not depend on the path taken by the particle. Also the work done by a conservative force is equal to the negative of change in potential energy during that process. For a proof of that, let's imagine two paths 1 and 2, both going from point A to point B. The variation of energy for the particle, taking path 1 from A to B and then path 2 backwards from B to A, is 0; thus, the work is the same in path 1 and 2, i.e., the work is independent of the path followed, as long as it goes from A to B.

For example, if a child slides down a frictionless slide, the work done by the gravitational force on the child from the top of the slide to the bottom will be the same no matter what the shape of the slide; it can be straight or it can be a spiral. The amount of work done only depends on the vertical displacement of the child.

Mathematical description

A force field F is called conservative if it meets any of these equivalent (proof) conditions:

1. The curl of F is zero:

2. The work, W, is zero for any simple closed path:

3. The force can be written as the gradient of a potential, :

Conservative force fields are curl-less as a direct consequence of Helmholtz decomposition. The term conservative force comes from the fact that when a conservative force exists, it conserves mechanical energy. The most familiar conservative forces are gravity, the electric force (in a time-independent magnetic field, see Faraday's law), and spring force.

Many forces (particularly those that depend on velocity) are not force fields. In these cases, the above three conditions are not mathematically equivalent. For example, the magnetic force satisfies condition 2 (since the work done by a magnetic field on a charged particle is always zero), but does not satisfy condition 3, and condition 1 is not even defined (the force is not a vector field, so one cannot evaluate its curl). Accordingly, some authors classify the magnetic force as conservative,^[1] while others do not.^[2] It should be emphasized that the magnetic force is an unusual case; most velocity-dependent forces, such as friction, do not satisfy any of the three conditions, and therefore are unambiguously nonconservative.

Nonconservative forces

Nonconservative forces arise due to neglected degrees of freedom. For instance, friction may be treated without resorting to the use of nonconservative forces by considering the motion of individual molecules; however that means every molecule's motion must be considered rather than handling it through statistical methods. For macroscopic systems the nonconservative approximation is far easier to deal with than millions of degrees of freedom. Examples of nonconservative forces are friction and non-elastic material stress.

See also

• Conservative vector field

Footnotes and references