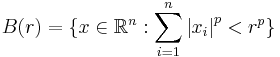Ball (mathematics)
In mathematics, a ball is the inside of a sphere; both concepts apply not only in the three-dimensional space but also for lower and higher dimensions, and for metric spaces in general.
Contents |
Balls in general metric spaces
Let (M,d) be a metric space, namely a set M with a metric (distance function) d. The open (metric) ball of radius r > 0 centered at a point p in M, usually denoted by 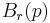 or
or 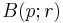 , is defined by
, is defined by
The closed (metric) ball, which may be denoted by ![B_r[p]](/2009-wikipedia_en_wp1-0.7_2009-05/I/3324cf338fb990b59e4bed0c2865ef83.png) or
or ![B[p;r]](/2009-wikipedia_en_wp1-0.7_2009-05/I/49db7fd12f4bd2d51c0dac4b46752266.png) , is defined by
, is defined by
Note in particular that a ball (open or closed) always includes p itself, since the definition requires r > 0.
The closure of the open ball 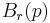 is usually denoted
is usually denoted 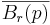 . While it is always the case that
. While it is always the case that 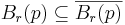 and
and ![B_r(p) \subseteq B_r[p]](/2009-wikipedia_en_wp1-0.7_2009-05/I/c4582b2b3bec6e48552d957b5450e47a.png) , it is not always the case that
, it is not always the case that ![\overline{ B_r(p) } = B_r[p]](/2009-wikipedia_en_wp1-0.7_2009-05/I/8916c3cb1a4111964b0d9a25a88250cd.png) . For example, in a metric space
. For example, in a metric space 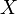 with the discrete metric, one has
with the discrete metric, one has 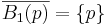 and
and ![B_1[p] = X](/2009-wikipedia_en_wp1-0.7_2009-05/I/4e7122a12a6dbb6c0f6b692265add2c0.png) , for any
, for any 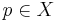 .
.
An (open or closed) unit ball is a ball of radius 1.
A subset of a metric space is bounded if it is contained in some ball. A set is totally bounded if, given any positive radius, it is covered by finitely many balls of that radius.
The open balls of a metric space are a basis for a topological space, whose open sets are all possible unions of open balls. This space is called the topology induced by the metric d.
Balls in normed vector spaces
Any normed vector space 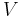 with norm
with norm 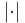 is also a metric space, with the metric
is also a metric space, with the metric  . In such spaces, every ball
. In such spaces, every ball 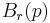 is a copy of the unit ball
is a copy of the unit ball 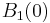 , scaled by
, scaled by  and translated by
and translated by 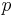 .
.
Euclidean norm
In particular, if 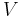 is n-dimensional Euclidean space with the ordinary (Euclidean) metric, every ball is the interior of an hypersphere (a hyperball). That is a bounded interval when n=1, the interior of a circle (a disk) when n=2, and the interior of a sphere when n=3.
is n-dimensional Euclidean space with the ordinary (Euclidean) metric, every ball is the interior of an hypersphere (a hyperball). That is a bounded interval when n=1, the interior of a circle (a disk) when n=2, and the interior of a sphere when n=3.
P-norm
In Cartesian space 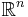 with the p-norm Lp, an open ball is the set
with the p-norm Lp, an open ball is the set
For n=2, in particular, the balls of L1 (often called the taxicab or Manhattan metric) are squares with the diagonals parallel to the coordinate axes; those of L∞ (the Chebyshev metric) are squares with the sides parallel to the coordinate axes. For other values of p, the balls are the interiors of Lamé curves (hypoellipses or hyperellipses).
For n=3, the balls of L1 are octahedra with axis-aligned body diagonals, those of L∞ are cubes with axis-aligned edges, and those of Lp with p> 2 are superellipsoids.
General convex norm
More generally, given any centrally symmetric, bounded, closed, and convex subset 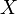 of
of 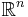 , one can define a metric on
, one can define a metric on 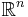 where the balls are all translated and uniformly scaled copies of
where the balls are all translated and uniformly scaled copies of 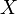 .
.
Topological balls
One may talk about balls in any topological space 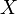 , not necessarily induced by a metric. An (open or closed) n-dimensional topological ball of
, not necessarily induced by a metric. An (open or closed) n-dimensional topological ball of 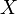 is any subset of
is any subset of 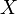 which is homeomorphic to an (open or closed) Euclidean n-ball. Topological n-balls are important in combinatorial topology, as the building blocks of cell complexes.
which is homeomorphic to an (open or closed) Euclidean n-ball. Topological n-balls are important in combinatorial topology, as the building blocks of cell complexes.
Any open topological n-ball is homeomorphic to the Cartesian space 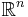 and to the open unit n-cube
and to the open unit n-cube 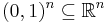 . Any closed topological n-ball is homeomorphic to the closed n-cube
. Any closed topological n-ball is homeomorphic to the closed n-cube ![[0,1]^n](/2009-wikipedia_en_wp1-0.7_2009-05/I/8b404eb306a7bcd23d0ec167aa7bcb37.png) .
.
An n-ball is homeomorphic to an m-ball if and only if n=m. The homeomorphisms between an open n-ball 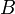 and
and 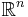 can be classified in two classes, that can be identified with the two possible topological orientations of
can be classified in two classes, that can be identified with the two possible topological orientations of 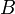 .
.
A topological n-ball need not be smooth; if it is smooth, it need not be diffeomorphic to an Euclidean n-ball.
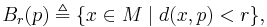
![B_r[p] \triangleq \{ x \in M \mid d(x,p) \le r \},](/2009-wikipedia_en_wp1-0.7_2009-05/I/1293cc05cd050e192ea744837457a7d8.png)