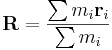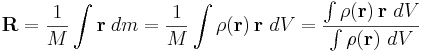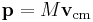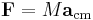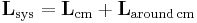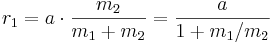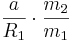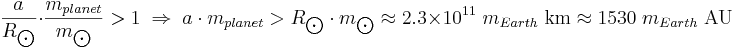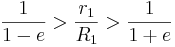Center of mass

The center of mass of a system of particles is a specific point at which, for many purposes, the system's mass behaves as if it were concentrated. The center of mass is a function only of the positions and masses of the particles that comprise the system. In the case of a rigid body, the position of its center of mass is fixed in relation to the object (but not necessarily in contact with it). In the case of a loose distribution of masses in free space, such as, say, shot from a shotgun, the position of the center of mass is a point in space among them that may not correspond to the position of any individual mass. In the context of an entirely uniform gravitational field, the center of mass is often called the center of gravity — the point where gravity can be said to act.

The center of mass of a body does not always coincide with its intuitive geometric center, and one can exploit this freedom. Engineers try to design a sports car's center of gravity as low as possible to make the car handle better. When high jumpers perform a "Fosbury Flop", they bend their body in such a way that it is possible for the jumper to clear the bar while his or her center of mass does not.^[1]

The so-called center of gravity frame (a less-preferred term for the center of momentum frame) is an inertial frame defined as the inertial frame in which the center of mass of a system is at rest.

1 Definition
2 Examples
3 History
4 Derivation of center of mass
5 Alternative Derivation
6 Rotation and centers of gravity
7 CM frame
8 Engineering
- 8.1 Aeronautical significance
9 Barycenter in astronomy
- 9.1 Animations
10 Locating the center of mass of an arbitrary 2D physical shape
11 Locating center of mass
12 Locating the center of mass of a composite shape
13 Locating the center of mass by tracing around the perimeter of the shape
14 See also
15 Notes
16 References
17 External links

Definition

The center of mass 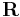$\mathbf{R}$ of a system of particles is defined as the average of their positions, 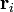$\mathbf{r}_i$ , weighted by their masses, $m_i$ :

$\mathbf{R} = { \sum m_i \mathbf{r}_i \over \sum m_i }$

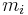For a continuous distribution with mass density 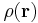$\rho(\mathbf{r})$ and total mass 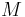$M$ , the sum becomes an integral:

$\mathbf R =\frac 1M \int \mathbf{r} \; dm = \frac 1M \int\rho(\mathbf{r})\, \mathbf{r} \ dV =\frac{\int\rho(\mathbf{r})\, \mathbf{r} \ dV}{\int\rho(\mathbf{r})\ dV}$

If an object has uniform density then its center of mass is the same as the centroid of its shape.

Examples

The center of mass of a two-particle system lies on the line connecting the particles (or, more precisely, their individual centers of mass). The center of mass is closer to the more massive object; for details, see barycenter below.
The center of mass of a ring is at the center of the ring (in the air).
The center of mass of a solid triangle lies on all three medians and therefore at the centroid, which is also the average of the three vertices.
The center of mass of a rectangle is at the intersection of the two diagonals.
In a spherically symmetric body, the center of mass is at the center. This approximately applies to the Earth: the density varies considerably, but it mainly depends on depth and less on the other two coordinates.
More generally, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.

History

The concept of center of gravity was first introduced by the ancient Greek mathematician, physicist, and engineer Archimedes of Syracuse. Archimedes showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point — their center of gravity. In work on floating bodies he demonstrated that the orientation of a floating object is the one that makes its center of gravity as low as possible. He developed mathematical techniques for finding the centers of gravity of objects of uniform density of various well-defined shapes, in particular a triangle, a hemisphere, and a frustum of a circular paraboloid.

In the Middle Ages, theories on the center of gravity were further developed by Abū Rayhān al-Bīrūnī, al-Razi (Latinized as Rhazes), Omar Khayyám, and al-Khazini.^[2]

Derivation of center of mass

The following equations of motion assume that there is a system of particles governed by internal and external forces. An internal force is a force caused by the interaction of the particles within the system. An external force is a force that originates from outside the system, and acts on one or more particles within the system. The external force need not be due to a uniform field.

For any system with no external forces, the center of mass moves with constant velocity. This applies for all systems with classical internal forces, including magnetic fields, electric fields, chemical reactions, and so on. More formally, this is true for any internal forces that satisfy the weak form of Newton's Third Law.

The total momentum for any system of particles is given by

$\mathbf{p}=M\mathbf{v}_\mathrm{cm}$

Where M indicates the total mass, and v_cm is the velocity of the center of mass. This velocity can be computed by taking the time derivative of the position of the center of mass.

An analogue to Newton's Second Law is

$\mathbf{F} = M\mathbf{a}_\mathrm{cm}$

Where F indicates the sum of all external forces on the system, and a_cm indicates the acceleration of the center of mass.

Letting the total internal force of the system.

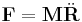
$\mathbf{F}=\mathbf{M}\ddot\mathbf{R}$

where 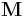$\mathbf{M}$ is the total mass of the system and 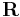$\mathbf{R}$ is a vector yet to be defined, since:

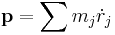
$\mathbf{p} = \sum{m_j\dot{r}_j}$

and

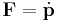
$\mathbf{F}=\dot\mathbf{p}$

then

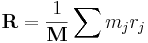
$\mathbf{R}=\frac{1}{\mathbf{M}}\sum{m_jr_j}$

We therefore have a vectorial definition for center of mass in terms of the total forces in the system. This is particularly useful for two-body systems.

Alternative Derivation

Consider first two bodies, with masses m₁ and m₂, and position vectors r₁ and r₂. Write M = m₁ + m₂ for the total mass of the 2-body system, and R for the position vector of the center of mass.

It is reasonable to require, for any system of masses, that the center of mass lie within the convex hull of the system. In particular, for a pair of mass points, this means that the tip of R must lie on the line segment joining the tips of r₁ and r₂. By geometry, R - r₁ = k(r₂ - R) for some positive constant k. Taking magnitudes on both sides of this equation, we get d₁ = kd₂, where d₁ is the distance from the center of mass to body 1, and d₂ is the distance from the center of mass to body 2. The constant k should obviously depend only on the masses m₁ and m₂, and we will examine the nature of this dependence.

Assuming the total mass M is nonzero, it is clear that if m₂ = 0, the center of mass should coincide with body 1, and d₁ = 0. This means d₂ = D, the total distance between the two bodies, and m₁ = M. Symmetry demands that these relations remain true when the subscripts 1 and 2 are interchanged everywhere.

The simplest model satisfying these requirements is the linear one, d₁ = (D/M)m₂ and d₂ = (D/M)m₁.

Under this model, we have k = d₁/d₂ = m₂/m₁. Therefore, after multiplying our vector equation by m₁, we find that m₁(R - r₁) = m₂(r₂ - R), or (m₁ + m₂)R = m₁r₁ + m₂r₂. Thus,

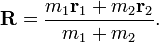
$\mathbf{R} = \frac{m_1 \mathbf{r}_1 + m_2 \mathbf{r}_2}{m_1 + m_2}.$

Now suppose there is a third body, of mass m₃ and position r₃. Temporarily break the symmetry between the three bodies, and define the 3-body center of mass as the 2-body center of mass determined by body 3 together with a single body of mass M₀ = m₁ + m₂ placed at the center of mass of bodies 1 and 2, whose position vector we now denote by R₀. The formula derived above gives

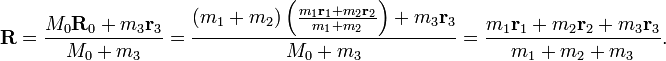
$\mathbf{R} = \frac{M_0 \mathbf{R}_0 + m_3 \mathbf{r}_3}{M_0 + m_3} = \frac{ (m_1 + m_2) \left( \frac{m_1 \mathbf{r}_1 + m_2 \mathbf{r}_2}{m_1 + m_2} \right) + m_3 \mathbf{r}_3}{M_0 + m_3} = \frac{m_1 \mathbf{r}_1 + m_2 \mathbf{r}_2 + m_3 \mathbf{r}_3}{m_1 + m_2 + m_3}.$

Since R turns out to be symmetric in the m_i and r_i, it would not have mattered had we started by combining bodies 2 and 3, or bodies 1 and 3, instead of bodies 1 and 2. This kind of reasoning clearly extends to any number of masses, and yields the formula

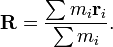
$\mathbf{R} = \frac{\sum m_i \mathbf{r}_i}{\sum m_i}.$

So our simple model of the 2-body center of mass uniquely and consistently determines the corresponding formula in any number of mass points. Writing M = m₁ + m₂ + ... + m_n, the above formula for the center of mass may be expressed in the form

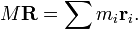
$M \mathbf{R} = \sum m_i \mathbf{r}_i.$

Differentiating both sides yields the principle that

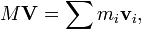
$M \mathbf{V} = \sum m_i \mathbf{v}_i,$

i.e., the sum of the momenta of a number of bodies is the momentum of their center of mass. It is this principle that gives precise expression to the intuitive notion that the system as a whole behaves like a mass of M placed at R, and justifies our simple linear model of the one-dimensional center of mass.

Rotation and centers of gravity

Diagram of an educational toy that balances on a point: the CM (C) settles below its support (P). Any object whose CM is below the fulcrum will not topple.

The suspending chair trick makes use of the human body's center of gravity, and the fact that it's surprisingly high.

The center of mass is often called the center of gravity because any uniform gravitational field g acts on a system as if the mass M of the system were concentrated at the center of mass R. This is seen in at least two ways:

The gravitational potential energy of a system is equal to the potential energy of a point particle having the same mass M located at R.
The gravitational torque on a system equals the torque of a force Mg acting at R:
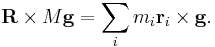
: $\mathbf{R} \times M\mathbf{g}=\sum_im_i \mathbf{r}_i \times \mathbf{g}.$

If the gravitational field acting on a body is not uniform, then the center of mass does not necessarily exhibit these convenient properties concerning gravity. As the situation is put in Feynman's influential textbook The Feynman Lectures on Physics:

"The center of mass is sometimes called the center of gravity, for the reason that, in many cases, gravity may be considered uniform. ...In case the object is so large that the nonparallelism of the gravitational forces is significant, then the center where one must apply the balancing force is not simple to describe, and it departs slightly from the center of mass. That is why one must distinguish between the center of mass and the center of gravity."

Many authors have been less careful, stating that when gravity is not uniform, "the center of gravity" departs from the CM. This usage seems to imply a well-defined "center of gravity" concept for non-uniform fields, but there is no such thing. Symon, in his textbook Mechanics, shows that the center of gravity of an extended body must always be defined relative to an external point, at which location resides a point mass that is exerting a gravitational force on the object in question. In fact, as Symon says:

"For two extended bodies, no unique centers of gravity can in general be defined, even relative to each other, except in special cases, as when the bodies are far apart, or when one of them is a sphere....The general problem of determining the gravitational forces between bodies is usually best treated by means of the concepts of the field theory of gravitation..."

Even when considering tidal forces on planets, it is sufficient to use centers of mass to find the overall motion. In practice, for non-uniform fields, one simply does not speak of a "center of gravity".^[3]

CM frame

Main article: Center of mass frame

The angular momentum vector for a system is equal to the angular momentum of all the particles around the center of mass, plus the angular momentum of the center of mass, as if it were a single particle of mass 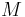$M$ :

$\mathbf{L}_\mathrm{sys} = \mathbf{L}_\mathrm{cm} + \mathbf{L}_\mathrm{around\,cm}$

This is a corollary of the Parallel Axis Theorem.

Engineering

Aeronautical significance

Main article: Center of gravity of an aircraft

The center of mass is an important point on an aircraft, which significantly affects the stability of the aircraft. To ensure the aircraft is safe to fly, it is critical that the center of gravity fall within specified limits. This range varies by aircraft, but as a rule of thumb it is centered about a point one quarter of the way from the wing leading edge to the wing trailing edge (the quarter chord point). If the center of mass is ahead of the forward limit, the aircraft will be less maneuverable, possibly to the point of being unable to rotate for takeoff or flare for landing. If the center of mass is behind the aft limit, the moment arm of the elevator is reduced, which makes it more difficult to recover from a stalled condition. The aircraft will be more maneuverable, but also less stable, and possibly so unstable that it is impossible to fly.

Barycenter in astronomy

The barycenter (or barycentre; from the Greek βαρύκεντρον) is the point between two objects where they balance each other. In other words, it is the center of gravity where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a star, both bodies are actually orbiting around a point that lies outside the center of the greater body. For example, the moon does not orbit the exact center of the earth, instead orbiting a point outside the earth's center (but well below the surface of the Earth) where their respective masses balance each other. The barycenter is one of the foci of the elliptical orbit of each body. This is an important concept in the fields of astronomy, astrophysics, and the like (see two-body problem).

In a simple two-body case, r₁, the distance from the center of the first body to the barycenter is given by:

$r_1 = a \cdot {m_2 \over m_1 + m_2} = {a \over 1 + m_1/m_2}$

where:

a is the distance between the two bodies' centers;

m₁ and m₂ are the masses of the two bodies.

r₁ is essentially the semi-major axis of the first body's orbit around the barycenter — and r₂ = a - r₁ the semi-major axis of the second body's orbit. Where the barycenter is located within the more massive body, that body will appear to "wobble" rather than following a discernible orbit.

The following table sets out some examples from our solar system. Figures are given rounded to three significant figures. The last two columns show R₁, the radius of the first (more massive) body, and r₁/R₁, the ratio of the distance to the barycenter and that radius: a value less than one shows that the barycenter lies inside the first body.

**Examples**
Larger body	m₁ (m_E=1)	Smaller body	m₂ (m_E=1)	a (km)	r₁ (km)	R₁ (km)	r₁/R₁
Remarks
Earth	1	Moon	0.0123	384,000	4,670	6,380	0.732
The Earth has a perceptible "wobble".
Pluto	0.0021	Charon	0.000,254 (0.121 m_Pluto)	19,600	2,110	1,150	1.83
Both bodies have distinct orbits around the barycenter, and as such Pluto and Charon were considered as a double planet by many before the redefinition of planet in August 2006.
Sun	333,000	Earth	1	150,000,000 (1 AU)	449	696,000	0.000,646
The Sun's wobble is barely perceptible.
Sun	333,000	Jupiter	318	778,000,000 (5.20 AU)	742,000	696,000	1.07
The Sun orbits a barycenter just above its surface.

If m₁ >> m₂ — which is true for the Sun and any planet — then the ratio r₁/R₁ approximates to:

${a \over R_1} \cdot {m_2 \over m_1}$

Hence, the barycenter of the Sun-planet system will lie outside the Sun only if:

${a \over R_{\bigodot}} \cdot {m_{planet} \over m_{\bigodot}} > 1 \; \Rightarrow \; {a \cdot m_{planet}} > {R_{\bigodot} \cdot m_{\bigodot}} \approx 2.3 \times 10^{11} \; m_{Earth} \; \mbox{km} \approx 1530 \; m_{Earth} \; \mbox{AU}$

That is, where the planet is heavy and far from the Sun.

If Jupiter had Mercury's orbit (57,900,000 km, 0.387 AU), the Sun-Jupiter barycenter would be only 5,500 km from the center of the Sun (r₁/R₁ ~ 0.08). But even if the Earth had Eris' orbit (68 AU), the Sun-Earth barycenter would still be within the Sun (just over 30,000 km from the center).

To calculate the actual motion of the Sun, you would need to sum all the influences from all the planets, comets, asteroids, etc. of the solar system (see n-body problem). If all the planets were aligned on the same side of the Sun, the combined center of mass would lie about 500,000 km above the Sun's surface.

The calculations above are based on the mean distance between the bodies and yield the mean value r₁. But all celestial orbits are elliptical, and the distance between the bodies varies between the apses, depending on the eccentricity, e. Hence, the position of the barycenter varies too, and it is possible in some systems for the barycenter to be sometimes inside and sometimes outside the more massive body. This occurs where:

${1 \over {1-e}} > {r_1 \over R_1} > {1 \over {1+e}}$

Note that the Sun-Jupiter system, with e_Jupiter = 0.0484, just fails to qualify: 1.05 ≯ 1.07 > 0.954.

Animations

Images are representative, not simulated.

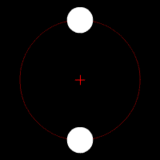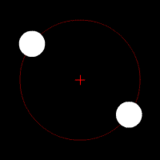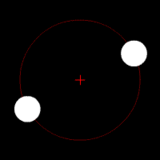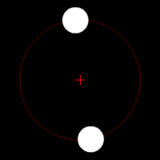Two bodies of similar mass orbiting around a common barycenter. (similar to the 90 Antiope system)	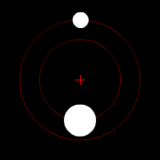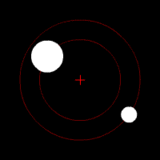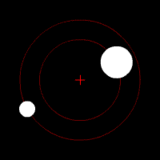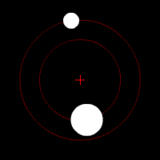Two bodies with a difference in mass orbiting around a common barycenter, as in the Pluto-Charon system.	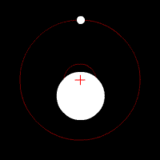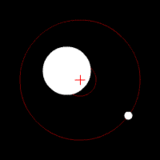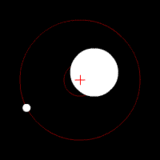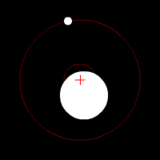Two bodies with a major difference in mass orbiting around a common barycenter (similar to the Earth-Moon system)	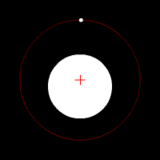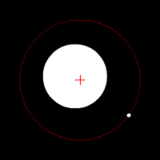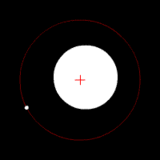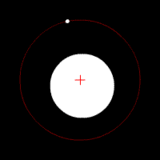Two bodies with an extreme difference in mass orbiting around a common barycenter (similar to the Sun-Earth system)
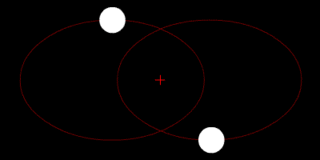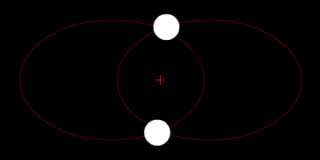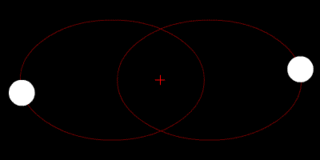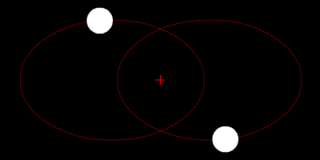Two bodies with similar mass orbiting around a common barycenter with elliptic orbits (a common situation for binary stars)

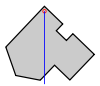
Locating the center of mass of an arbitrary 2D physical shape

This method is useful when one wishes to find the center of gravity of a complex planar object with unknown dimensions.


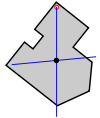Step 1: An arbitrary 2D shape.	Step 2: Suspend the shape from a location near an edge. Drop a plumb line and mark on the object.	Step 3: Suspend the shape from another location not too close to the first. Drop a plumb line again and mark. The intersection of the two lines is the center of gravity.

Locating center of mass

This is a method of determining the center of mass of an L-shaped object.

CG of L-shaped object

Divide the shape into two rectangles, as shown in fig 2. Find the center of masses of these two rectangles by drawing the diagonals. Draw a line joining the center of masses. The center of mass of the shape must lie on this line AB.
Divide the shape into two other rectangles, as shown in fig 3. Find the center of masses of these two rectangles by drawing the diagonals. Draw a line joining the center of masses. The center of mass of the L-shape must lie on this line CD.
As the center of mass of the shape must lie along AB and also along CD, it is obvious that it is at the intersection of these two lines, at O. The point O might not lie inside the L-shaped object.

Locating the center of mass of a composite shape

This method is useful when you wish to find the center of gravity of an object that is easily divided into elementary shapes, whose centers of mass are easy to find (see List of centroids). We will only be finding the center of mass in the x direction here. The same procedure may be followed to locate the center of mass in the y direction.

COG 1.svg The shape. It is easily divided into a square, triangle, and circle. Note that the circle will have negative area.

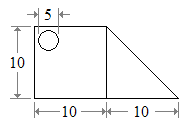COG 2.png From the List of centroids, we note the coordinates of the individual centroids.

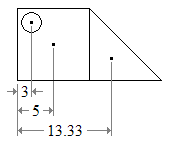COG 3.png From equation 1 above:

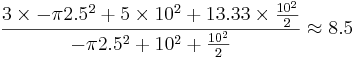$\frac{3 \times -\pi2.5^2 + 5 \times 10^2 + 13.33 \times \frac{10^2}{2}}{ -\pi2.5^2 + 10^2 + \frac{10^2}{2}} \approx 8.5$ units.

The center of mass of this figure is at a distance of 8.5 units from the left corner of the figure.

Locating the center of mass by tracing around the perimeter of the shape

A direct development of the planimeter known as an integraph, or integerometer (though a better term is probably moment planimeter), can be used to establish the position of the center of mass of an irregular shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to ensure the ship would not capsize. See Locating the center of mass by mechanical means.

Notes

↑ Van Pelt, Michael (2005). Space Tourism: Adventures in Earth Orbit and Beyond. Springer. pp. 185. ISBN 0387402136.
↑ Salah Zaimeche PhD (2005). Merv, Foundation for Science Technology and Civilization.
↑ Symon, K. R. (1971). Mechanics, 3rd ed., Reading: Addison-Wesley.

References

Feynman, Richard; Robert Leighton, Matthew Sands (1963). The Feynman Lectures on Physics. Addison Wesley. ISBN 0-201-02116-1.
Goldstein, Herbert; Charles Poole, John Safko (2002). Classical Mechanics (3e ed.). Addison Wesley. ISBN 0-201-65702-3.
Kleppner, Daniel; Robert Kolenkow (1973). An Introduction to Mechanics (2e ed.). McGraw-Hill. ISBN 0-07-035048-5.
Marion, Jerry; Stephen Thornton (1995). Classical Dynamics of Particles and Systems (4e ed.). Harcourt. ISBN 0-03-097302-3.
Murray, Carl; Stanley Dermott (1999). Solar System Dynamics. Cambridge UP. ISBN 0-521-57295-9.
Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
Symon, Keithe R. (1971). Mechanics (3rd edition ed.). Addison-Wesley. ISBN 0-201-07392-7.
Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.

External links

barycenter fold by Paul Niquette.
Center of Gravity Encyclopaedia Britannica.
Locating the center of mass by mechanical means.
Measuring Center of Gravity Space Electronics, manufacturer of center of gravity measurement instruments.
Motion of the Center of Mass shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
The solar system's barycenter Simulations showing the effect each planet contributes to the solar system's barycenter