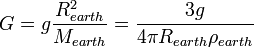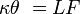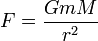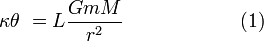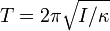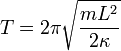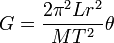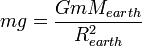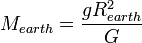Cavendish experiment

Artist's conception of Cavendish conducting his experiment. He performed the experiment inside a closed shed and observed the result from outside through a telescope. The opening in the wall was added by the artist to show the apparatus.

The Cavendish experiment, done in 1797 – 1798 by Henry Cavendish, was the first experiment to measure the force of gravity between masses in the laboratory,[1] and the first to yield accurate values for the gravitational constant and the mass of the Earth.[2][3] However, these were derived by others from Cavendish's result, which was a value for the Earth's density.[4] The experiment was devised sometime before 1783[5] by John Michell,[6] who constructed a torsion balance apparatus for it. However, Michell died in 1793 without completing the work, and after his death the apparatus passed to Francis John Hyde Wollaston and then to Henry Cavendish, who rebuilt the apparatus but kept close to Michell's original plan. Cavendish then carried out a series of measurements with the equipment, and reported his results in the Philosophical Transactions of the Royal Society in 1798.[7]

Contents

The experiment

The apparatus constructed by Cavendish was a torsion balance made of a six-foot wooden rod suspended from a wire, with a 2-inch (51 mm) diameter 1.61 pound lead sphere attached to each end. Two 12 inch 348 pound lead balls were located near the smaller balls, about 9 inches away, and held in place with a separate suspension system.[8] The experiment measured the faint gravitational attraction between the small balls and the larger ones.

Vertical section drawing of Cavendish's torsion balance instrument including the building in which it was housed. The large balls were hung from a frame so they could be rotated into position next to the small balls by a pulley from outside. Figure 1 of Cavendish's paper.
Detail showing torsion balance arm (m), large ball (W), small ball (x), and isolating box (ABCDE).

The two large balls were positioned on alternate sides of the horizontal wooden arm of the balance. Their mutual attraction to the small balls caused the arm to rotate, twisting the wire supporting the arm. The arm stopped rotating when it reached an angle where the twisting force of the wire balanced the combined gravitational force of attraction between the large and small lead spheres. By measuring the angle of the rod, and knowing the twisting force (torque) of the wire for a given angle, Cavendish was able to determine the force between the pairs of masses. Since the gravitational force of the Earth on the small ball could be measured directly by weighing it, the ratio of the two forces allowed the density of the earth to be calculated, using Newton's law of gravitation.

Cavendish found that the Earth's density was 5.448 ± 0.033 times that of water (due to a simple arithmetic error, found in 1821 by F. Baily, the erroneous value 5.48 ± 0.038 appears in his paper).[9]

To find the wire's torsion coefficient, the torque exerted by the wire for a given angle of twist, Cavendish timed the natural oscillation period of the balance rod as it rotated slowly clockwise and counterclockwise against the twisting of the wire. The period was about 7 minutes. The torsion coefficient could be calculated from this and the mass and dimensions of the balance. Actually, the rod was never at rest; Cavendish had to measure the deflection angle of the rod while it was oscillating.[10]

Cavendish's equipment was remarkably sensitive for its time.[9] The force involved in twisting the torsion balance was very small, 1.47 x 10–7 N,[11] about 1/50,000,000 of the weight of the small balls[12] or roughly the weight of a large grain of sand.[13] To prevent air currents and temperature changes from interfering with the measurements, Cavendish placed the entire apparatus in a wooden box about 2 feet (0.61 m) thick, 10 feet (3.0 m) tall, and 10 feet (3.0 m) wide, all in a closed shed on his estate. Through two holes in the walls of the shed, Cavendish used telescopes to observe the movement of the torsion balance's horizontal rod. The motion of the rod was only about 0.16 inch.[14] Cavendish was able to measure this small deflection to an accuracy of better than one hundredth of an inch using vernier scales on the ends of the rod.[15]

Cavendish's experiment was repeated by Reich (1838), Baily (1843), Cornu & Baille (1878), and many others. Its accuracy was not exceeded for 97 years, until C. V. Boys (1895) experiment. In time, Michell's torsion balance became the dominant technique for measuring the gravitational constant (G), and most contemporary measurements still use variations of it. This is why Cavendish's experiment became the Cavendish experiment.[16]

Did Cavendish determine G?

It is not unusual to find books that state erroneously that Cavendish's purpose was determining the gravitational constant (G),[17][18][19][20][21] and this mistake has been pointed out by several authors.[22][23][24][25] In actuality, Cavendish's only goal was to measure the density of the Earth; he called it 'weighing the world'. The method Cavendish used to calculate the Earth's density consists in measuring the force on a small ball caused by a large ball of known mass, and comparing it with the force on the small ball caused by the Earth, so the Earth can be calculated to be N times more massive than the large ball without the need to obtain a numeric value for G.[23] The gravitational constant does not appear in Cavendish's paper, and there is no indication that he regarded it as a goal of his experiment. One of the first references to G is in 1873, 75 years after Cavendish's work.[26]

In Cavendish's time, G did not have the importance among scientists that it has today; it was simply a proportionality constant in Newton's law.[27] The purpose of measuring the force of gravity was instead to determine the Earth's density. This was a much-desired quantity in 18th-century astronomy, since once the Earth's density was known, the densities of the Moon, Sun, and the other planets could be found from it.[28]

A further complication is that up through the mid-nineteenth century, scientists did not use a specific unit of measurement for force.[23] This unnecessarily tied G to the mass of the Earth, as opposed to G being recognized as a universal constant. However, even though Cavendish did not report a value for G, the results of his experiment allowed it to be determined. During the late 1800s, as scientists began to recognize G as a fundamental constant of nature, they calculated it from Cavendish's accurate results, thus:[29]

G = g\frac{R_{earth}^2}{M_{earth}} = \frac{3g}{4\pi R_{earth}\rho_{earth}}\,

After converting to SI units, Cavendish's value for the Earth's density, 5.45 g cm−3, gives G = 6.74 × 10−11 m3 kg−1 sec−2, which is within 1% of the currently accepted value.

Derivation of G and the Earth's mass

For the definitions of terms, see the drawing below and the table at the end of this section.

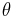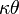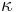The following is not the method Cavendish used, but shows how modern physicists would use his results.[30][31][32] From Hooke's law, the torque on the torsion wire is proportional to the deflection \theta of the balance. The torque is \kappa\theta where \kappa is the torsion coefficient. However, the torque can also be written as a product of the attractive forces and the distance to the wire. Since there are two pairs of balls, each experiencing force F at a distance L / 2 from the axis of the balance, the torque is LF. Equating the two formulas for torque gives the following:

\kappa\theta\ = LF \,

For F, Newton's law of universal gravitation is used to express the attractive force between the large and small balls:

Diagram of torsion balance
F = \frac{G m M}{r^2}\,

Substituting F into the first equation above gives

\kappa\theta\ = L\frac{GmM}{r^2} \qquad\qquad\qquad(1)\,

To find the torsion coefficient (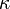\kappa\,) of the wire, Cavendish measured the natural resonant oscillation period T of the torsion balance:

T = 2\pi\sqrt{I/\kappa}

Assuming the mass of the torsion beam itself is negligible, the moment of inertia of the balance is just due to the small balls:

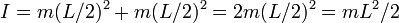I = m(L/2)^2 + m(L/2)^2 = 2m(L/2)^2 = mL^2/2\,,

and so:

T = 2\pi\sqrt{\frac{mL^2}{2\kappa}}\,

Solving this for 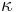\kappa, substituting into (1), and rearranging for G, the result is:

G = \frac{2 \pi^2 L r^2}{M T^2} \theta\,

Once G has been found, the attraction of an object at the Earth's surface to the Earth itself can be used to calculate the Earth's mass and density:

mg = \frac{GmM_{earth}}{R_{earth}^2}\,
M_{earth} = \frac{gR_{earth}^2}{G}\,
\rho_{earth} = \frac{M_{earth}}{4 \pi R_{earth}^3/3} = \frac{3g}{4 \pi R_{earth} G}\,
Definition of terms
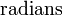\theta\, \mbox{radians}\, Deflection of torsion balance beam from its rest position
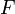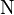F\, \mbox{N}\, Gravitational force between masses M and m
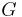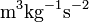G\, \mbox{m}^3 {\mbox{kg}}^{-1} \mbox{s}^{-2}\, Gravitational constant
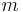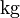m\, \mbox{kg}\, Mass of small lead ball
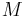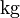M\, \mbox{kg}\, Mass of large lead ball
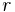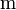r\, \mbox{m}\, Distance between centers of large and small balls when balance is deflected
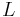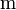L\, \mbox{m}\, Length of torsion balance beam between centers of small balls
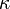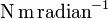\kappa\, \mbox{N}\,\mbox{m}\,\mbox{radian}^{-1}\, Torsion coefficient of suspending wire
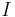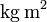I\, \mbox{kg}\,\mbox{m}^2\, Moment of inertia of torsion balance beam
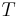T\, \mbox{s}\, Period of oscillation of torsion balance
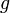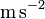g\, \mbox{m}\,\mbox{s}^{-2}\, Acceleration of gravity at the surface of the Earth
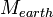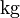M_{earth}\, \mbox{kg}\, Mass of the Earth
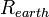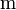R_{earth}\, \mbox{m}\, Radius of the Earth
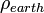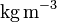\rho_{earth}\, \mbox{kg}\,\mbox{m}^{-3}\, Density of the Earth

References

Notes

  1. ↑ Boys 1894 p.355
  2. ↑ Encyclopaedia Britannica 1910 p.385 'The aim [of experiments like Cavendish's] may be regarded either as the determination of the mass of the Earth,...conveniently expressed...as its "mean density", or as the determination of the "gravitation constant", G'. Cavendish's experiment is generally described today as a measurement of G (Clotfelter 1987 p.210).
  3. ↑ Many sources state erroneously that this was the first measurement of G (or the Earth's density), such as Feynman, Richard P. (1963) (– Scholar search), Lectures on Physics, Vol.1, Addison-Wesley, pp. p.6–7, ISBN 0201021161, http://books.google.com/books?id=k6MQrphL-NIC&pg=PA28 . There were previous measurements, chiefly Bouguer (1740) and Maskelyne (1774), but they were very inaccurate (Poynting 1894)(Encyclopedia Britannica 1910).
  4. ↑ Clotfelter 1987, p.210
  5. ↑ McCormmach & Jungnickel 1996, p.336: A 1783 letter from Cavendish to Michell contains '...the earliest mention of weighing the world'. Not clear whether 'earliest mention' refers to Cavendish or Michell.
  6. ↑ Cavendish 1798, p.59 Cavendish gives full credit to Michell for devising the experiment
  7. ↑ Cavendish, H. 'Experiments to determine the Density of the Earth', Philosophical Transactions of the Royal Society of London, (part II) 88 p.469-526 (21 June 1798), reprinted in Cavendish 1798
  8. ↑ Cavendish 1798, p.59
  9. ↑ 9.0 9.1 Poynting 1894, p.45
  10. ↑ Cavendish 1798, p.64
  11. ↑ Boys 1894 p.357
  12. ↑ Cavendish 1798 p. 60
  13. ↑ A 2 mm sand grain weighs ~13 mg. Theodoris, Marina (2003). "Mass of a Grain of Sand". The Physics Factbook.
  14. ↑ Cavendish 1798, p. 99, Result table, (scale graduations = 1/20 inch) The total deflection shown in most trials was twice this since he compared the deflection with large balls on opposite sides of the balance beam.
  15. ↑ Cavendish 1798, p.63
  16. ↑ McCormmach & Jungnickel 1996, p.341
  17. ↑ Halliday, David; Resnick, Robert (1993), Fundamentals of Physics, John Wiley & Sons, pp. p.418, ISBN 0471147311, http://books.google.com/books?id=-AjnmJHPiKMC&pg=PA418  'The apparatus used in 1798 by Henry Cavendish to measure the gravitational constant'
  18. ↑ Feynman, Richard P. (1963) (– Scholar search), Lectures on Physics, Vol.1, Addison-Wesley, pp. p.6–7, ISBN 0201021161, http://books.google.com/books?id=k6MQrphL-NIC&pg=PA28  'Cavendish claimed he was weighing the Earth, but what he was measuring was the coefficient G...'
  19. ↑ Feynman, Richard P. (1967) (– Scholar search), The Character of Physical Law, MIT Press, pp. p.28, ISBN 0262560038, http://books.google.com/books?id=k6MQrphL-NIC&pg=PA28  'Cavendish was able to measure the force, the two masses, and the distance, and thus determine the gravitational constant G'
  20. ↑ Cavendish Experiment, Harvard Lecture Demonstrations, Harvard Univ, http://www.fas.harvard.edu/~scdiroff/lds/NewtonianMechanics/CavendishExperiment/CavendishExperiment.html, retrieved on 2007-08-26 . '[the torsion balance was]...modified by Cavendish to measure G.'
  21. ↑ Shectman, Jonathan (2003), Groundbreaking Experiments, Inventions, and Discoveries of the 18th Century, Greenwood, pp. p.xlvii, ISBN 0313320152, http://books.google.com/books?id=SsbChdIiflsC&pg=PAxlvii  'Cavendish calculates the gravitational constant, which in turn gives him the mass of the earth...'
  22. ↑ Clotfelter 1987
  23. ↑ 23.0 23.1 23.2 McCormmach & Jungnickel 1996, p.337
  24. ↑ Hodges 1999
  25. ↑ Lally 1999
  26. ↑ Cornu, A. and Baille, J. B. (1873), Mutual determination of the constant of attraction and the mean density of the earth, C. R. Acad. Sci., Paris Vol. 76, 954-958.
  27. ↑ Boys 1894, p.330 In this lecture before the Royal Society, Boys introduces G and argues for its acceptance
  28. ↑ Poynting 1894, p.4
  29. ↑ MacKenzie 1900, p.vi
  30. ↑ Cavendish Experiment, Harvard Lecture Demonstrations, Harvard Univ.
  31. ↑ Poynting 1894, p.41
  32. ↑ Clotfelter 1987 p.212 explains Cavendish's original method of calculation

External links