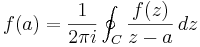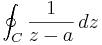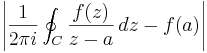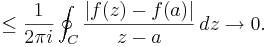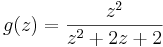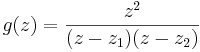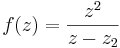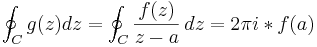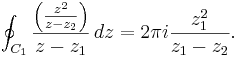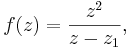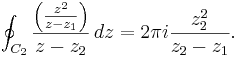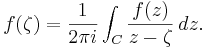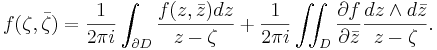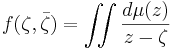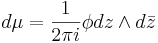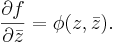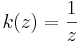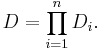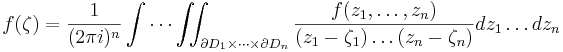Cauchy's integral formula

In mathematics, Cauchy's integral formula, named after Augustin Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk. It can also be used to obtain integral formulas for all derivatives of a holomorphic function. The analytic significance of Cauchy's formula is that it shows that in complex analysis "differentiation is equivalent to integration": thus complex differentation, like integration, behaves well under uniform limits, a result which is not true in real analysis.

Contents

Theorem

Suppose U is an open subset of the complex plane C, f : U → C is a holomorphic function and the closed disk D = { z : | z − z0| ≤ r} is completely contained in U. Let C be the circle forming the boundary of D. Then for every a in the interior of D:

f(a) = {1 \over 2\pi i} \oint_C {f(z) \over z-a}\, dz

where the contour integral is taken counter-clockwise.

The proof of this statement uses the Cauchy integral theorem and similarly only requires f to be complex differentiable. Since the denominator of the integrand in Cauchy's integral formula can be expanded as a power series in the variable (a - z0), it follows that holomorphic functions are analytic. In particular f is actually infinitely differentiable, with

f^{(n)}(a) = {n! \over 2\pi i} \oint_C {f(z) \over (z-a)^{n+1}}\, dz.

This formula is sometimes referred to as Cauchy's differentiation formula.

The circle C can be replaced by any closed rectifiable curve in U which has winding number one about a. Moreover, as for the Cauchy integral theorem, it is sufficient to require that f be holomorphic in the open region enclosed by the path and continuous on its closure.

Proof sketch

By using the Cauchy integral theorem, one can show that the integral over C (or the closed rectifiable curve) is equal to the same integral taken over an arbitrarily small circle around a. Since f(z) is continuous, we can choose a circle small enough on which f(z) is arbitrarily close to f(a). On the other hand, the integral

\oint_C { {1 \over z-a} \,dz}

over any circle C centered at a is 2πi. This can be calculated directly via parametrization (integration by substitution) z = a + \varepsilon e^{it} where 0 ≤ t ≤ 2π and ε is the radius of the circle.

Letting ε → 0 gives the desired estimate

\left | \frac{1}{2 \pi i} \oint_C { {f(z) \over z-a} \,dz} - f(a) \right |
\leq \frac{1}{2 \pi i} \oint_C \frac{ |f(z) - f(a)| } {z-a} \,dz \rightarrow 0.

Example

Surface of the absolute value of the function g(z) = z2 / (z2 + 2z + 2) and its singularities, with the contours described in the text.

Consider the function

g(z)={z^2 \over z^2+2z+2}

and the contour described by |z| = 2, call it C.

To find the integral of g(z) around the contour, we need to know the singularities of g(z). Observe that we can rewrite g as follows:

g(z)={z^2 \over (z-z_1)(z-z_2)}

where z_1=-1+i, z_2=-1-i.

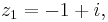
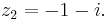
Clearly the poles become evident, their moduli are less than 2 and thus lie inside the contour and are subject to consideration by the formula. By the Cauchy-Goursat theorem, we can express the integral around the contour as the sum of the integral around z1 and z2 where the contour is a small circle around each pole. Call these contours C1 around z1 and C2 around z2.

Now, around C1, f is analytic (since the contour does not contain the other singularity), and this allows us to write f in the form we require, namely:

f(z)={z^2 \over z-z_2}

and now

\oint_C {g(z) dz} = \oint_C {f(z) \over z-a}\, dz=2\pi i*f(a)
\oint_{C_1} {\left({z^2 \over z-z_2}\right) \over z-z_1}\,dz=2\pi i{z_1^2 \over z_1-z_2}.

Doing likewise for the other contour:

f(z)={z^2 \over z-z_1},
\oint_{C_2} {\left({z^2 \over z-z_1}\right) \over z-z_2}\,dz=2\pi i{z_2^2 \over z_2-z_1}.

The integral around the original contour C then is the sum of these two integrals:

\begin{align}\oint_C {z^2 \over z^2+2z+2}\,dz &{}= \oint_{C_1} {\left({z^2 \over z-z_2}\right) \over z-z_1}\,dz + \oint_{C_2} {\left({z^2 \over z-z_1}\right) \over z-z_2}\,dz \\ \\ &{}= 2\pi i\left({z_1^2 \over z_1-z_2}+{z_2^2 \over z_2-z_1}\right) \\ \\ &{}=2\pi i(-2) \\ \\ &{}=-4\pi i.\end{align}

Consequences

The integral formula has broad applications. First, it implies that a function which is holomorphic in an open set is in fact infinitely differentiable there. Furthermore, it is an analytic function, meaning that it can be represented as a power series. The proof of this uses the dominated convergence theorem and the geometric series applied to

f(\zeta) = \frac{1}{2\pi i}\int_C \frac{f(z)}{z-\zeta}\,dz.

The formula is also used to prove the residue theorem, which is a result for meromorphic functions, and a related result, the argument principle. It is known from Morera's theorem that the uniform limit of holomorphic functions is holomorphic. This can also be deduced from Cauchy's integral formula: indeed the formula also holds in the limit and the integrand, and hence the integral, can be expanded as a power series. In addition the Cauchy formulas for the higher order derivatives show that all these derivatives also converge uniformly.

The analog of the Cauchy integral formula in real analysis is the Poisson integral formula for harmonic functions; many of the results for holomorphic functions carry over to this setting. No such results, however, are valid for more general classes of differentiable or real analytic functions. For instance, the existence of the first derivative of a real function need not imply the existence of higher order derivatives, nor in particular the analyticity of the function. Likewise, the uniform limit of a sequence of (real) differentiable functions may fail to be differentiable, or may be differentiable but with a derivative which is not the limit of the derivatives of the members of the sequence.

Generalizations

Smooth functions

A version of Cauchy's integral formula holds for smooth functions as well, as it is based on Stokes' theorem. Let D be a disc in C and suppose that f is a complex-valued C1 function on the closure of D. Then (Hörmander 1966, Theorem 1.2.1)

f(\zeta,\bar{\zeta}) = \frac{1}{2\pi i}\int_{\partial D} \frac{f(z,\bar{z})dz}{z-\zeta} + \frac{1}{2\pi i}\iint_D \frac{\partial f}{\partial \bar{z}}\frac{dz\wedge d\bar{z}}{z-\zeta}.

One may use this representation formula to solve the inhomogeneous Cauchy-Riemann equations in D. Indeed, if φ is a function in D, then a particular solution f of the equation

\frac{\partial f}{\partial\bar{z}} = \phi(z,\bar{z})

is given by

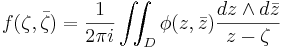f(\zeta,\bar{\zeta}) = \frac{1}{2\pi i}\iint_D \phi(z,\bar{z})\frac{dz\wedge d\bar{z}}{z-\zeta}.

More rigorously (Hörmander 1966, Theorem 1.2.2), if μ is a complex (finite) measure of compact support on C then

f(\zeta,\bar{\zeta}) = \iint \frac{d\mu(z)}{z-\zeta}

is a holomorphic function outside the support of μ. Moreover, if in an open set D,

d\mu = \frac{1}{2\pi i}\phi dz\wedge d\bar{z}

for some φ ∈ Ck(D) (k≥1), then 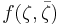f(\zeta,\bar{\zeta}) is also in Ck(D) and satisfies the equation

\frac{\partial f}{\partial\bar{z}} = \phi(z,\bar{z}).

The first conclusion is, succinctly, that the convolution μ*k(z) of a compactly supported measure with the Cauchy kernel

k(z) = \frac{1}{z}

is a holomorphic function off the support of μ. The second conclusion asserts that the Cauchy kernel is a fundamental solution of the Cauchy-Riemann equations.

Several variables

In several complex variables, the Cauchy integral formula can be generalized to polydiscs (Hörmander 1966, Theorem 2.2.1). Let D be the polydisc given as the Cartesian product of n open discs D1, ..., Dn:

D = \prod_{i=1}^n D_i.

Suppose that f is a holomorphic function in D continuous on the closure of D. Then

f(\zeta) = \frac{1}{(2\pi i)^n}\int\cdots\iint_{\partial D_1\times\dots\times\partial D_n} \frac{f(z_1,\dots,z_n)}{(z_1-\zeta_1)\dots(z_n-\zeta_n)}dz_1\dots dz_n

where ζ=(ζ1,...,ζn) ∈ D.

See also

References

External links