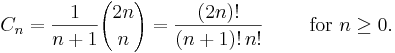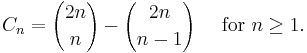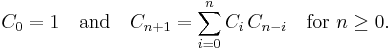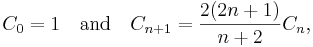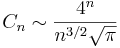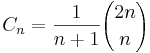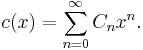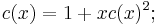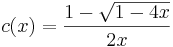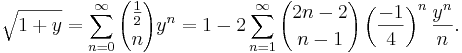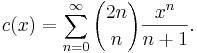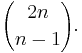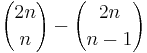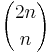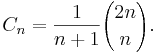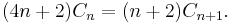Catalan number

In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named for the Belgian mathematician Eugène Charles Catalan (1814–1894).

The nth Catalan number is given directly in terms of binomial coefficients by

C_n = \frac{1}{n+1}{2n\choose n} = \frac{(2n)!}{(n+1)!\,n!} \qquad\mbox{ for }n\ge 0.

The first Catalan numbers (sequence A000108 in OEIS) for n = 0, 1, 2, 3, … are

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

Contents

Properties

An alternative expression for Cn is

C_n = {2n\choose n} - {2n\choose n-1} \quad\mbox{ for }n\ge 1.

This shows that Cn is a natural number, which is not a priori obvious from the first formula given. This expression forms the basis for André's proof of the correctness of the formula (see below under second proof).

The Catalan numbers satisfy the recurrence relation

C_0 = 1 \quad \mbox{and} \quad C_{n+1}=\sum_{i=0}^{n}C_i\,C_{n-i}\quad\mbox{for }n\ge 0.

They also satisfy:

C_0 = 1 \quad \mbox{and} \quad C_{n+1}=\frac{2(2n+1)}{n+2}C_n,

which can be a more efficient way to calculate them.

Asymptotically, the Catalan numbers grow as

C_n \sim \frac{4^n}{n^{3/2}\sqrt{\pi}}

in the sense that the quotient of the nth Catalan number and the expression on the right tends towards 1 for n → ∞. (This can be proved by using Stirling's approximation for n!.)

The only Catalan numbers 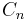C_n which are odd are those for which 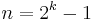n=2^k-1. All others are even.

Applications in combinatorics

There are many counting problems in combinatorics whose solution is given by the Catalan numbers. The book Enumerative Combinatorics: Volume 2 by combinatorialist Richard P. Stanley contains a set of exercises which describe 66 different interpretations of the Catalan numbers. Following are some examples, with illustrations of the cases C3 = 5 and C4 = 14.

XXXYYY     XYXXYY     XYXYXY     XXYYXY     XXYXYY.
((()))     ()(())     ()()()     (())()     (()())
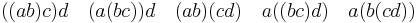
((ab)c)d \quad (a(bc))d \quad(ab)(cd) \quad a((bc)d) \quad a(b(cd))
Catalan number binary tree example.png

If the leaves are labelled, we have the quadruple factorial numbers.

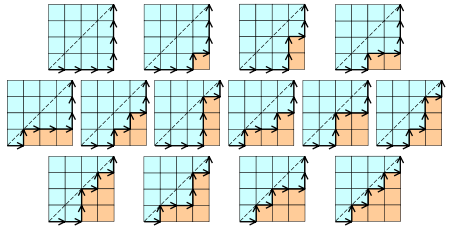
Catalan number 4x4 grid example.svg
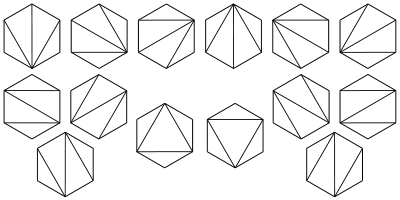
Catalan-Hexagons-example.svg
Catalan stairsteps 4.svg

Proof of the formula

There are several ways of explaining why the formula

C_n = \frac{1}{n+1}{2n\choose n}

solves the combinatorial problems listed above. The first proof below uses a generating function. The second and third proofs are examples of bijective proofs; they involve literally counting a collection of some kind of object to arrive at the correct formula.

First proof

We first observe that many of the combinatorial problems listed above satisfy the recurrence relation

C_0 = 1 \quad \mbox{and} \quad C_{n+1}=\sum_{i=0}^{n}C_i\,C_{n-i}\quad\mbox{for }n\ge 0.

For example, every Dyck word w of length ≥ 2 can be written in a unique way in the form

w = Xw1Yw2

with (possibly empty) Dyck words w1 and w2.

The generating function for the Catalan numbers is defined by

c(x)=\sum_{n=0}^\infty C_n x^n.

The two recurrence relations together can then be summarized in generating function form by the relation

c(x)=1+xc(x)^2;\,

in other words, this equation follows from the recurrence relations by expanding both sides into power series. On the one hand, the recurrence relations uniquely determine the Catalan numbers; on the other hand, the generating function solution

c(x) = \frac{1-\sqrt{1-4x}}{2x}

has a power series at 0 and its coefficients must therefore be the Catalan numbers. (Since the other solution has a pole at'0, this reasoning doesn't apply to it.)

The square root term can be expanded as a power series using the identity

\sqrt{1+y} = \sum_{n=0}^\infty {\frac12 \choose n} y^n = 1 - 2\sum_{n=1}^\infty {2n-2 \choose n-1} \left(\frac{-1}{4}\right)^n \frac{y^n}{n}.

This is a special case of Newton's generalized binomial theorem; as with the general theorem, it can be proved by computing derivatives to produce its Taylor series. Setting y = -4x and substituting this power series into the expression for c(x) and shifting the summation index n by 1, the expansion simplifies to

c(x) = \sum_{n=0}^\infty {2n \choose n} \frac{x^n}{n+1}.

The coefficients are now the desired formula for Cn.

Second proof

This proof depends on a trick known as the reflection principle (not to be confused with the Schwarz reflection principle in complex analysis). The reflection principle has been widely, but incorrectly, attributed to André; it is actually due to Aebly and Mirimanoff[1]. It is most easily expressed in terms of the "monotonic paths which do not cross the diagonal" problem (see above).

Figure 1. The green portion of the path is flipped.

Suppose we are given a monotonic path in an n × n grid that does cross the diagonal. Find the first edge in the path that lies above the diagonal, and flip the portion of the path occurring after that edge, along a line parallel to the diagonal. (In terms of Dyck words, we are starting with a sequence of n X's and n Y's which is not a Dyck word, and exchanging all X's with Y's after the first Y that violates the Dyck condition.) The resulting path is a monotonic path in an (n − 1) × (n + 1) grid. Figure 1 illustrates this procedure; the green portion of the path is the portion being flipped.

Since every monotonic path in the (n − 1) × (n + 1) grid must cross the diagonal at some point, every such path can be obtained in this fashion in precisely one way. The number of these paths is equal to

{2n\choose n-1}.

Therefore, to calculate the number of monotonic n × n paths which do not cross the diagonal, we need to subtract this from the total number of monotonic n × n paths, so we finally obtain

{2n\choose n}-{2n\choose n-1}

which is the nth Catalan number Cn.

Third proof

The following bijective proof, while being more involved than the previous one, provides a more natural explanation for the term n + 1 appearing in the denominator of the formula for Cn.

Figure 2. A path with exceedance 5.

Suppose we are given a monotonic path, which may happen to cross the diagonal. The exceedance of the path is defined to be the number of pairs of edges which lie above the diagonal. For example, in Figure 2, the edges lying above the diagonal are marked in red, so the exceedance of the path is 5.

Now, if we are given a monotonic path whose exceedance is not zero, then we may apply the following algorithm to construct a new path whose exceedance is one less than the one we started with.

The following example should make this clearer. In Figure 3, the black circle indicates the point where the path first crosses the diagonal. The black edge is X, and we swap the red portion with the green portion to make a new path, shown in the second diagram.

Figure 3. The green and red portions are being exchanged.

Notice that the exceedance has dropped from three to two. In fact, the algorithm will cause the exceedance to decrease by one, for any path that we feed it.

Figure 4. All monotonic paths in a 3×3 grid, illustrating the exceedance-decreasing algorithm.

It is also not difficult to see that this process is reversible: given any path P whose exceedance is less than n, there is exactly one path which yields P when the algorithm is applied to it.

This implies that the number of paths of exceedance n is equal to the number of paths of exceedance n − 1, which is equal to the number of paths of exceedance n − 2, and so on, down to zero. In other words, we have split up the set of all monotonic paths into n + 1 equally sized classes, corresponding to the possible exceedances between 0 and n. Since there are

{2n\choose n}

monotonic paths, we obtain the desired formula

C_n = \frac{1}{n+1}{2n\choose n}.

Figure 4 illustrates the situation for n = 3. Each of the 20 possible monotonic paths appears somewhere in the table. The first column shows all paths of exceedance three, which lie entirely above the diagonal. The columns to the right show the result of successive applications of the algorithm, with the exceedance decreasing one unit at a time. Since there are five rows, C3 = 5.

Fourth proof

This proof uses the triangulation definition of Catalan numbers to establish a relation between Cn and Cn+1. Given a polygon P with n+ 2 sides, first mark one of its sides as the base. If P is then triangulated, we can further choose and orient one of its 2n+1 edges. There are (4n+2)Cn such decorated triangulations. Now given a polygon Q with n+3 sides, again mark one of its sides as the base. If Q is triangulated, we can further mark one of the sides other than the base side. There are (n+2)Cn+1 such decorated triangulations. Then there is a simple bijection between these two kinds of decorated triangulations: We can either collapse the triangle in Q whose side is marked, or in reverse expand the oriented edge in P to a triangle and mark its new side. Thus

(4n+2)C_n = (n+2)C_{n+1}.

The binomial formula for Cn follows immediately from this relation and the initial condition C1 = 1.

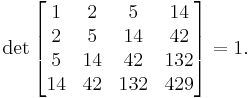
Hankel matrix

The n×n Hankel matrix whose (i, j) entry is the Catalan number Ci+j-2 has determinant 1, regardless of the value of n. For example, for n = 4 we have

\det\begin{bmatrix}1 & 1 & 2 & 5 \\ 1 & 2 & 5 & 14 \\ 2 & 5 & 14 & 42 \\ 5 & 14 & 42 & 132\end{bmatrix} = 1.

Note that if the entries are "shifted", namely the Catalan numbers Ci+j-1, the determinant is still 1, regardless of the size of n. For example, for n = 4 we have

\det\begin{bmatrix}1 & 2 & 5 & 14 \\ 2 & 5 & 14 & 42 \\ 5 & 14 & 42 & 132 \\ 14 & 42 & 132 & 429 \end{bmatrix} = 1.

The Catalan numbers form the unique sequence with this property.

Quadruple factorial

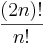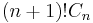The quadruple factorial is given by \frac{(2n)!}{n!}, or \left(n+1\right)! C_n. This is the solution to labelled variants of the above combinatorics problems. It is entirely distinct from the multifactorials.

History

The Catalan sequence was first described in the 18th century by Leonhard Euler, who was interested in the number of different ways of dividing a polygon into triangles. The sequence is named after Eugène Charles Catalan, who discovered the connection to parenthesized expressions during his exploration of the Towers of Hanoi puzzle. The counting trick for Dyck words was found by D. André in 1887.

See also

  • Associahedron
  • Bertrand's ballot theorem
  • Binomial transform
  • Catalan's problem
  • Catalan–Mersenne number
  • List of factorial and binomial topics
  • Narayana number
  • Tamari lattice

Notes

  1. ↑ Renault, Marc. (2008): Lost (and found) in translation: André's actual method and its application to the generalized ballot problem, Amer. Math. Monthly, vol. 115, no. 4, pp. 358–363.

References

External links