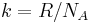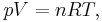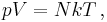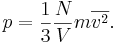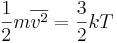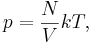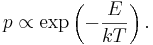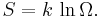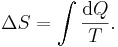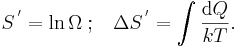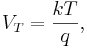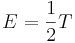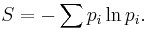Boltzmann constant

Values of k	Units
1.380 6504(24)×10⁻²³	J·K^-1
8.617 343(15)×10⁻⁵	eV·K^-1
1.3807×10⁻¹⁶	erg·K^-1
For details, see Value in different units below.

The Boltzmann constant (k or k_B) is the physical constant relating energy at the particle level with temperature observed at the bulk level. It is the gas constant divided by the Avogadro constant:

$\ k = R/N_A$

It has the same units as entropy. It is named after the Austrian physicist Ludwig Boltzmann.

1 Bridge from macroscopic to microscopic physics
2 Role in the equipartition of energy
- 2.1 Application to simple gas thermodynamics
3 Role in Boltzmann factors
4 Role in definition of entropy
5 Role in semiconductor physics: the thermal voltage
6 Boltzmann's constant in Planck units
7 Historical note
8 Value in different units
9 References

Bridge from macroscopic to microscopic physics

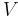Boltzmann's constant $k$ is a bridge between macroscopic and microscopic physics. Macroscopically, the ideal gas law states that, for an ideal gas, the product of pressure $p$ and volume $V$ is proportional to the product of amount of substance 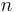$n$ (in number of moles) and absolute temperature $T$ .

$\ pV = nRT,$

where

$\ R$

is the gas constant (8.314472 J K⁻¹·mol⁻¹).

Introducing Boltzmann's constant transforms the ideal gas law into an equation about the microscopic properties of molecules,

$p V = N k T \,,$

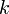where $N$ is the number of molecules of gas, and $k$ is Boltzmann's constant.

Role in the equipartition of energy

Given a thermodynamic system at an absolute temperature T, the thermal energy carried by each microscopic "degree of freedom" in the system is on the order of magnitude of kT/2 (i.e., about 2.07×10⁻²¹ J, or 0.013 eV at room temperature).

Application to simple gas thermodynamics

In classical statistical mechanics, this average is predicted to hold exactly for homogeneous ideal gases. Monatomic ideal gases possess 3 degrees of freedom per atom, corresponding to the three spatial directions, which means a thermal energy of 1.5kT per atom. As indicated in the article on heat capacity, this corresponds very well with experimental data. The thermal energy can be used to calculate the root mean square speed of the atoms, which is inversely proportional to the square root of the atomic mass. The root mean square speeds found at room temperature accurately reflect this, ranging from 1370 m/s for helium, down to 240 m/s for xenon.

Kinetic theory gives the average pressure p for an ideal gas as

$p = \frac{1}{3}\frac{N}{V} m {\overline{v^2}}.$

Substituting that the average translational kinetic energy is

$\frac{1}{2}m \overline{v^2} = \frac{3}{2} k T$

gives

$p = \frac{N}{V} k T,$

so the ideal gas equation is regained.

The ideal gas equation is also followed quite well for molecular gases; but the form for the heat capacity is more complicated, because the molecules possess new internal degrees of freedom, as well as the three degrees of freedom for movement of the molecule as a whole. Diatomic gases, for example, possess in total approximately 5 degrees of freedom per molecule. (Furthermore, these additional degrees of freedom may be further complicated by quantum mechanics -- see the article on heat capacity for details.)

Role in Boltzmann factors

More generally, systems in equilibrium with a reservoir of heat at temperature T have probabilities of occupying states with energy E weighted by the corresponding Boltzmann factor:

$p \propto \exp\left(-\frac{E}{kT}\right).$

Again, it is the energy-like quantity kT which takes central importance.

Consequences of this include (in addition to the results for ideal gases above), for example the Arrhenius equation of simple chemical kinetics.

Role in definition of entropy

Main article: Boltzmann's entropy formula

In statistical mechanics, the entropy S of an isolated system at thermodynamic equilibrium is defined as the natural logarithm of Ω, the number of distinct microscopic states available to the system given the macroscopic constraints (such as a fixed total energy E):

$S = k \, \ln \Omega.$

This equation, which relates the microscopic details of the system (via Ω) to its macroscopic state (via the entropy S), is the central idea of statistical mechanics. Such is its importance that it is inscribed on Boltzmann's tombstone.

The constant of proportionality k appears in order to make the statistical mechanical entropy equal to the classical thermodynamic entropy of Clausius:

$\Delta S = \int \frac{\mathrm{d}Q}{T}.$

One could choose instead a rescaled entropy in microscopic terms such that

${S^{\,'} = \ln \Omega} \;�; \; \; \; \Delta S^{\,'} = \int \frac{\mathrm{d}Q}{kT}.$

This is a rather more natural form; and this rescaled entropy exactly corresponds to Shannon's subsequent information entropy, and could thereby have avoided much unnecessary subsequent confusion between the two.

The characteristic energy kT is thus the heat required to increase the rescaled entropy by one nat.

Role in semiconductor physics: the thermal voltage

In semiconductors, the relationship between the flow of electrical current and the electrostatic potential across a p-n junction depends on a characteristic voltage called the thermal voltage, denoted V_T. The thermal voltage depends on absolute temperature T (in kelvins) as

$V_T = { kT \over q },$

where q is the magnitude of the electrical charge (in coulombs) on the electron (see elementary charge) with a value 1.602 176 487 ×10⁻¹⁹ C . Using the unit of electronvolt, the Boltzmann constant relating temperature to energy can be expressed as 8.617 343(15)×10⁻⁵ eV/K, making it easy to calculate that at room temperature (T ≈ 300 K), the value of the thermal voltage is approximately 25.85 millivolts ≈ 26 mV (Google calculator). See also semiconductor diodes.

Boltzmann's constant in Planck units

Planck's system of natural units is one system constructed such that the Boltzmann constant is 1. This gives

${ E = \frac{1}{2} T } \$

as the average kinetic energy of a gas molecule per degree of freedom; and makes the definition of thermodynamic entropy coincide with that of information entropy:

$S = - \sum p_i \ln p_i.$

The value chosen for the Planck unit of temperature is that corresponding to the energy of the Planck mass—a staggering 1.41679×10³² K.

Historical note

Although Boltzmann first linked entropy and probability in 1877, it seems the relation was never expressed with a specific constant until Max Planck first introduced k , and gave an accurate value for it, in his derivation of the law of black body radiation in December 1900. The iconic terse form of the equation S = k log W on Boltzmann's tombstone is in fact due to Planck, not Boltzmann.

As Planck wrote in his 1918 Nobel Prize lecture,

"This constant is often referred to as Boltzmann's constant, although, to my knowledge, Boltzmann himself never introduced it — a peculiar state of affairs, which can be explained by the fact that Boltzmann, as appears from his occasional utterances, never gave thought to the possibility of carrying out an exact measurement of the constant. Nothing can better illustrate the positive and hectic pace of progress which the art of experimenters has made over the past twenty years, than the fact that since that time, not only one, but a great number of methods have been discovered for measuring the mass of a molecule with practically the same accuracy as that attained for a planet." [1]

Before 1900, equations involving Boltzmann factors were not written using the energies per molecule and Boltzmann's constant, but rather using the gas constant R, and macroscopic energies for macroscopic quantities of the substance; as for convenience is still generally the case in chemistry to this day.

Value in different units

Values of k	Units	Comments
1.380 6504(24)×10⁻²³	J/K	SI units, 2002 CODATA value
8.617 343(15)×10⁻⁵	eV/K	1 electronvolt = 1.602 176 53(14)×10⁻¹⁹ J 1/k_B = 11 604.51(2) K/eV
6.336 281(73)×10⁻⁶	Ryd/K	1 Rydberg = 13.6 eV
1.3807×10⁻¹⁶	erg/K

The digits in parentheses are the standard measurement uncertainty in the last two digits of the measured value.

The constant can also be expressed in terms of energy per mole instead of energy per entity (such as 1.99 cal·mol⁻¹·K⁻¹); for historical reasons it is then called the gas constant and given the symbol R.

Since k is a constant of proportionality of temperature and energy, the numerical value of k depends on the choice of units for energy and temperature. The Kelvin temperature scale was chosen to conveniently divide up the liquid range of water into one hundred intervals. The very small numerical value of k merely reflects the small energy in joules required to increase a particle's energy through 1 K. The physically fundamental idea is the characteristic energy kT of a particular temperature.

The numerical value of k provides a mapping from this characteristic microscopic energy E to the macroscopically-derived temperature scale T = E/k. On the other hand, the Planck units of temperature and energy are defined in such a way that k=1. If we choose to measure temperature in units of energy then Boltzmann's constant would not be needed at all.^[1]

References

Boltzmann's constant CODATA value at NIST
Peter J. Mohr, and Barry N. Taylor, "CODATA recommended values of the fundamental physical constants: 1998", Rev. Mod. Phys., Vol 72, No. 2, April 2000

↑ Kalinin, M; Kononogov, S, "Boltzmann's Constant, the Energy Meaning of Temperature, and Thermodynamic Irreversibility", Measurement Techniques, pp632-636, vol 48, no 7, July 2005.