Bijection

In mathematics, a bijection, or a bijective function is a function f from a set X to a set Y with the property that, for every y in Y, there is exactly one x in X such that
f(x) = y.
Alternatively, f is bijective if it is a one-to-one correspondence between those sets; i.e., both one-to-one (injective) and onto (surjective). (One-to-one function means one-to-one correspondence (i.e., bijection) to some authors, but injection to others.)
For example, consider the function succ, defined from the set of integers 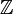 to
to 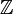 , that to each integer x associates the integer succ(x) = x + 1. For another example, consider the function sumdif that to each pair (x,y) of real numbers associates the pair sumdif(x,y) = (x + y, x − y).
, that to each integer x associates the integer succ(x) = x + 1. For another example, consider the function sumdif that to each pair (x,y) of real numbers associates the pair sumdif(x,y) = (x + y, x − y).
A bijective function from a set to itself is also called a permutation.
The set of all bijections from X to Y is denoted as X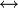 Y.
Y.
Bijective functions play a fundamental role in many areas of mathematics, for instance in the definition of isomorphism (and related concepts such as homeomorphism and diffeomorphism), permutation group, projective map, and many others.
Contents |
Composition and inverses
A function f is bijective if and only if its inverse relation f −1 is a function. In that case, f −1 is also a bijection.
The composition g o f of two bijections f X
X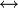 Y and g
Y and g Y
Y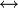 Z is a bijection. The inverse of g o f is (g o f)−1 = (f −1) o (g−1).
Z is a bijection. The inverse of g o f is (g o f)−1 = (f −1) o (g−1).

On the other hand, if the composition g o f of two functions is bijective, we can only say that f is injective and g is surjective.
A relation f from X to Y is a bijective function if and only if there exists another relation g from Y to X such that g o f is the identity function on X, and f o g is the identity function on Y. Consequently, the sets have the same cardinality.
Bijections and cardinality
If X and Y are finite sets, then there exists a bijection between the two sets X and Y if and only if X and Y have the same number of elements. Indeed, in axiomatic set theory, this is taken as the very definition of "same number of elements", and generalising this definition to infinite sets leads to the concept of cardinal number, a way to distinguish the various sizes of infinite sets.
Examples and counterexamples
- For any set X, the identity function idX from X to X, defined by idX(x) = x, is bijective.
- The function f from the real line R to R defined by f(x) = 2x + 1 is bijective, since for each y there is a unique x = (y − 1)/2 such that f(x) = y.
- The exponential function g : R
 R, with g(x) = ex, is not bijective: for instance, there is no x in R such that g(x) = −1, showing that g is not surjective. However if the codomain is changed to be the positive real numbers R+ = (0,+∞), then g becomes bijective; its inverse is the natural logarithm function ln.
R, with g(x) = ex, is not bijective: for instance, there is no x in R such that g(x) = −1, showing that g is not surjective. However if the codomain is changed to be the positive real numbers R+ = (0,+∞), then g becomes bijective; its inverse is the natural logarithm function ln. - The function h : R
 [0,+∞) with h(x) = x² is not bijective: for instance, h(−1) = h(+1) = 1, showing that h is not injective. However, if the domain too is changed to [0,+∞), then h becomes bijective; its inverse is the positive square root function.
[0,+∞) with h(x) = x² is not bijective: for instance, h(−1) = h(+1) = 1, showing that h is not injective. However, if the domain too is changed to [0,+∞), then h becomes bijective; its inverse is the positive square root function. 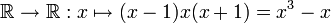 is not a bijection because −1, 0, and +1 are all in the domain and all map to 0.
is not a bijection because −1, 0, and +1 are all in the domain and all map to 0.![\mathbb{R} \to [-1,1]�: x \mapsto \sin(x)](/2009-wikipedia_en_wp1-0.7_2009-05/I/f394b7f7d2d83a77b9bb91de61c91a1f.png) is not a bijection because π/3 and 2π/3 are both in the domain and both map to (√3)/2.
is not a bijection because π/3 and 2π/3 are both in the domain and both map to (√3)/2.
Properties
- A function f from the real line R to R is bijective if and only if its plot is intersected by any horizontal line at exactly one point.
- If X is a set, then the bijective functions from X to itself, together with the operation of functional composition (o), form a group, the symmetric group of X, which is denoted variously by S(X), SX, or X! (the last reads "X factorial").
- For a subset A of the domain with cardinality |A| and subset B of the codomain with cardinality |B|, one has the following equalities:
- |f(A)| = |A| and |f−1(B)| = |B|.
- If X and Y are finite sets with the same cardinality, and f: X → Y, then the following are equivalent:
-
- f is a bijection.
- f is a surjection.
- f is an injection.
- At least for a finite set S, there is a bijection between the set of possible total orderings of the elements and the set of bijections from S to S. That is to say, the number of permutations (another name for bijections) of elements of S is the same as the number of total orderings of that set -- namely, n!.
Bijections and category theory
Formally, bijections are precisely the isomorphisms in the category Set of sets and functions. However, the bijections are not always the isomorphisms. For example, in the category Top of topological spaces and continuous functions, the isomorphisms must be homeomorphisms in addition to being bijections.
See also
- category theory
- injective function
- symmetric group
- surjective function
- Bijective numeration
- Bijective proof