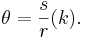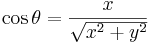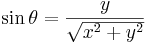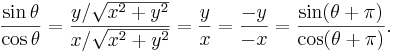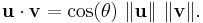Angle

"∠", the angle symbol.

In geometry and trigonometry, an angle (in full, plane angle) is the figure formed by two rays sharing a common endpoint, called the vertex of the angle (Sidorov 2001). The magnitude of the angle is the "amount of rotation" that separates the two rays, and can be measured by considering the length of circular arc swept out when one ray is rotated about the vertex to coincide with the other (see "Measuring angles", below). Where there is no possibility of confusion, the term "angle" is used interchangeably for both the geometric configuration itself and for its angular magnitude (which is simply a numerical quantity).

The word angle comes from the Latin word angulus, meaning "a corner". The word angulus is a diminutive, of which the primitive form, angus, does not occur in Latin. Cognate words are the Latin angere, meaning "to compress into a bend" or "to strangle", the Greek ἀγκύλος (ankylοs), meaning "crooked, curved," and the English word "ankle." All three are connected with the Proto-Indo-European root *ank-, meaning "to bend" or "bow" (Slocum 2007).

Contents

History

Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. According to Proclus an angle must be either a quality or a quantity, or a relationship. The first concept was used by Eudemus, who regarded an angle as a deviation from a straight line; the second by Carpus of Antioch, who regarded it as the interval or space between the intersecting lines; Euclid adopted the third concept, although his definitions of right, acute, and obtuse angles are certainly quantitative.

Measuring angles

The angle θ is the quotient of s and r.

In order to measure an angle θ, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The length of the arc s is then divided by the radius of the circle r, and possibly multiplied by a scaling constant k (which depends on the units of measurement that are chosen):

\theta = \frac{s}{r}(k).

The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed then the arc length changes in the same proportion, so the ratio s/r is unaltered.

In many geometrical situations, angles that differ by an exact multiple of a full circle are effectively equivalent (it makes no difference how many times a line is rotated through a full circle because it always ends up in the same place). However, this is not always the case. For example, when tracing a curve such as a spiral using polar coordinates, an extra full turn gives rise to a quite different point on the curve.

Units

Angles are considered dimensionless, since they are defined as the ratio of lengths. There are, however, several units used to measure angles, depending on the choice of the constant k in the formula above. Of these units, treated in more detail below, the degree and the radian are by far the most common.

With the notable exception of the radian, most units of angular measurement are defined such that one full circle (i.e. one revolution) is equal to n units, for some whole number n. For example, in the case of degrees, n = 360. A full circle of n units is obtained by setting k = n/(2π) in the formula above. (Proof. The formula above can be rewritten as k = θr/s. One full circle, for which θ = n units, corresponds to an arc equal in length to the circle's circumference, which is 2πr, so s = 2πr. Substituting n for θ and 2πr for s in the formula, results in k = nr/(2πr) = n/(2π).)

θ = s/r rad = 1 rad.

Positive and negative angles

A convention universally adopted in mathematical writing is that angles given a sign are positive angles if measured anticlockwise, and negative angles if measured clockwise, from a given line. If no line is specified, it can be assumed to be the x-axis in the Cartesian plane. In many geometrical situations a negative angle of −θ is effectively equivalent to a positive angle of "one full rotation less θ". For example, a clockwise rotation of 45° (that is, an angle of −45°) is often effectively equivalent to an anticlockwise rotation of 360° − 45° (that is, an angle of 315°).

In three dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined relative to some reference, which is typically a vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie.

In navigation, bearings are measured from north, increasing clockwise, so a bearing of 45 degrees is north-east. Negative bearings are not used in navigation, so north-west is 315 degrees.

Approximations

These measurements clearly depend on the individual subject, and the above should be treated as rough approximations only.

Identifying angles

In mathematical expressions, it is common to use Greek letters (α, β, γ, θ, φ, ...) to serve as variables standing for the size of some angle. (To avoid confusion with its other meaning, the symbol π is typically not used for this purpose.) Lower case roman letters (a, b, c, ...) are also used. See the figures in this article for examples.

In geometric figures, angles may also be identified by the labels attached to the three points that define them. For example, the angle at vertex A enclosed by the rays AB and AC (i.e. the lines from point A to point B and point A to point C) is denoted ∠BAC or BÂC. Sometimes, where there is no risk of confusion, the angle may be referred to simply by its vertex ("angle A").

Potentially, an angle denoted, say, ∠BAC might refer to any of four angles: the clockwise angle from B to C, the anticlockwise angle from B to C, the clockwise angle from C to B, or the anticlockwise angle from C to B, where the direction in which the angle is measured determines its sign (see Positive and negative angles). However, in many geometrical situations it is obvious from context that the positive angle less than or equal to 180° degrees is meant, and no ambiguity arises. Otherwise, a convention may be adopted so that ∠BAC always refers to the anticlockwise (positive) angle from B to C, and ∠CAB to the anticlockwise (positive) angle from C to B.

Types of angles

Right angle.
Reflex angle.
The complementary angles a and b (b is the complement of a, and a is the complement of b).
Acute (a), obtuse (b), and straight (c) angles. Here, a and b are supplementary angles.

A formal definition

Using trigonometric functions

A Euclidean angle is completely determined by the corresponding right triangle. In particular, if 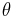\theta is a Euclidean angle, it is true that

\cos \theta = \frac{x}{\sqrt{x^2 + y^2}}

and

\sin \theta = \frac{y}{\sqrt{x^2 + y^2}}

for two numbers x and y. So an angle in the Euclidean plane can be legitimately given by two numbers x and y.

To the ratio y/x there correspond two angles in the geometric range 0 < θ < 2π, since

\frac{\sin \theta}{\cos \theta } = \frac{y/\sqrt{x^2 + y^2}}{x/\sqrt{x^2 + y^2}} = \frac{y}{x} = \frac{-y}{-x} = \frac{\sin (\theta + \pi)}{\cos (\theta + \pi) }.

Using rotations

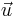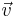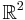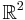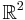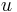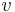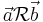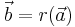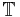Suppose we have two unit vectors \vec{u} and \vec{v} in the euclidean plane \mathbb{R}^2. Then there exists one positive isometry (a rotation), and one only, from \mathbb{R}^2 to \mathbb{R}^2 that maps u onto v. Let r be such a rotation. Then the relation \vec{a}\mathcal{R}\vec{b} defined by \vec{b}=r(\vec{a}) is an equivalence relation and we call angle of the rotation r the equivalence class \mathbb{T}/\mathcal{R}, where \mathbb{T} denotes the unit circle of 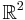\mathbb{R}^2. The angle between two vectors will simply be the angle of the rotation that maps one onto the other. We have no numerical way of determining an angle yet. 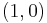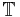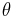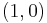To do this, we choose the vector (1,0), then for any point M on \mathbb{T} at distance \theta from (1,0) (on the circle), let 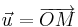\vec{u}=\overrightarrow{OM}. 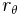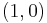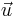If we call r_\theta the rotation that transforms (1,0) into \vec{u}, then \left[r_\theta\right]\mapsto\theta is a bijection, which means we can identify any angle with a number between 0 and 2\pi\,.

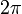Angles between curves

The angle between the two curves is defined as the angle between the tangents A and B at P

The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—amphicyrtic (Gr. ἀμφί, on both sides, κυρτόσ, convex) or cissoidal (Gr. κισσόσ, ivy), biconvex; xystroidal or sistroidal (Gr. ξυστρίσ, a tool for scraping), concavo-convex; amphicoelic (Gr. κοίλη, a hollow) or angulus lunularis, biconcave.

The dot product and generalisation

In the Euclidean plane, the angle θ between two vectors u and v is related to their dot product and their lengths by the formula

\mathbf{u} \cdot \mathbf{v} = \cos(\theta)\ \|\mathbf{u}\|\ \|\mathbf{v}\|.

This allows one to define angles in any real inner product space, replacing the Euclidean dot product · by the Hilbert space inner product \langle\cdot,\cdot\rangle.

Angles in Riemannian geometry

In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gij are the components of the metric tensor G,

\cos \theta = \frac{g_{ij}U^iV^j} {\sqrt{ \left| g_{ij}U^iU^j \right| \left| g_{ij}V^iV^j \right|}}.

Angles in geography and astronomy

In geography, the location of any point on the Earth can be identified using a geographic coordinate system. This system specifies the latitude and longitude of any location in terms of angles subtended at the centre of the Earth, using the equator and (usually) the Greenwich meridian as references.

In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several astronomical coordinate systems, where the references vary according to the particular system. Astronomers measure the angular separation of two stars by imagining two lines through the centre of the Earth, each intersecting one of the stars. The angle between those lines can be measured, and is the angular separation between the two stars.

Astronomers also measure the apparent size of objects as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5°, when viewed from Earth. One could say, "The Moon subtends an angle of half a degree." The small-angle formula can be used to convert such an angular measurement into a distance/size ratio.

See also

References

External links