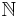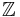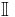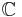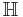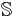Algebraic number

In mathematics, an algebraic number is a complex number that is a root of a non-zero polynomial in one variable with rational (or equivalently, integer) coefficients. Complex numbers such as pi that are not algebraic are said to be transcendental, and are infinitely more numerous within the complex number field.

1 Examples
2 Properties
3 The field of algebraic numbers
4 Numbers defined by radicals
5 Algebraic integers
6 Special classes of algebraic number
7 References

Examples

The rational numbers, those expressed as the ratio of two whole numbers b and a, a not equal to zero, satisfy the above definition because x = −b/a is derived from (and satisfies) ax + b = 0. (In general, a or b can be negative, as can x).^[1]
Some irrational numbers are algebraic and some are not:

The numbers √2 and ³√3/2 are algebraic since they are the roots of x² − 2 = 0 and 8x³ − 3 = 0, respectively.
The golden ratio φ is algebraic since it is a root of the polynomial x² − x − 1 = 0.
The numbers π and e are not algebraic numbers (see the Lindemann–Weierstrass theorem);^[2] hence they are transcendental.

The constructible numbers (those that, starting with a unit, can be constructed with straightedge and compass, e.g. the square root of 2) are algebraic.
The quadratic surds (roots of a quadratic equation ax² + bx + c = 0 with integral coefficents a, b, and c) are algebraic numbers. Thus those complex numbers derived from ax² + bx + c = 0 — those corresponding to the case when the exponent n = 2 — are called quadratic numbers, or quadratic integers as the case may be.
Gaussian integers — those complex numbers a + bi where both a and b are integers are also quadratic integers.
When the lead coefficient of a polynomial is 1, any value x that satisfies the polynomial is said to be an algebraic integer. Note that an "algebraic integer" need not be a counting number such as 1, 2, 3, ... or a negative counterpart.

This definition comes from the notion that x = −b/a satisfies ax + b = 0, and when a = 1 then x = −b (i.e. b here being a positive or negative counting number or 0). But observe that from 1·x² + 4 = 0, x = 2i and −2i. So these two x are "algebraic integers" as well. This applies for any value of lead-exponent n. (See more below).

Properties

The set of algebraic numbers is countable (enumerable).^[3]
Hence, the set of algebraic numbers has Lebesgue measure zero (as a subset of the complex numbers), i.e. "almost all" complex numbers are not algebraic.
Given an algebraic number, there is a unique monic polynomial (with rational coefficients) of least degree that has the number as a root. This polynomial is called its minimal polynomial. If its minimal polynomial has degree n, then the algebraic number is said to be of degree n. An algebraic number of degree 1 is a rational number.
All algebraic numbers are computable and therefore definable.

The field of algebraic numbers

The sum, difference, product and quotient of two algebraic numbers is again algebraic, and the algebraic numbers therefore form a field, sometimes denoted by 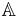$\mathbb{A}$ (which may also denote the adele ring) or $\overline{\mathbb{Q}}$ . Every root of a polynomial equation whose coefficients are algebraic numbers is again algebraic. This can be rephrased by saying that the field of algebraic numbers is algebraically closed. In fact, it is the smallest algebraically closed field containing the rationals, and is therefore called the algebraic closure of the rationals.

Numbers defined by radicals

All numbers which can be obtained from the integers using a finite number of additions, subtractions, multiplications, divisions, and taking n^th roots (where n is a positive integer) are algebraic. The converse, however, is not true: there are algebraic numbers which cannot be obtained in this manner. All of these numbers are solutions to polynomials of degree ≥ 5. This is a result of Galois theory (see Quintic equations and the Abel–Ruffini theorem). An example of such a number is the unique real root of x⁵ − x − 1 = 0 (which is approximately 1.167303978261418684256).

Algebraic integers

Main article: algebraic integer

An algebraic integer is a number which is a root of a polynomial with integer coefficients (that is, an algebraic number) with leading coefficient 1 (a monic polynomial). Examples of algebraic integers are 3√2 + 5, 6i − 2 and (1 + i√3)/2.

The sum, difference and product of algebraic integers are again algebraic integers, which means that the algebraic integers form a ring. The name algebraic integer comes from the fact that the only rational numbers which are algebraic integers are the integers, and because the algebraic integers in any number field are in many ways analogous to the integers. If K is a number field, its ring of integers is the subring of algebraic integers in K, and is frequently denoted as O_K. These are the prototypical examples of Dedekind domains.

Special classes of algebraic number

Gaussian integer
Eisenstein integer
Quadratic irrational
Fundamental unit
Root of unity
Gaussian period
Pisot-Vijayaraghavan number
Salem number

References

↑ Some of the following examples come from Hardy and Wright 1972:159-160 and pp. 178-179
↑ Also Liouville's theorem can be used to "produce as many examples of transcendentals numbers as we please," cf Hardy and Wright p. 161ff
↑ Hardy and Wright 1972:160

Artin, Michael (1991), Algebra, Prentice Hall, MR1129886, ISBN 0-13-004763-5
Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory, Graduate Texts in Mathematics, 84 (Second ed.), Berlin, New York: Springer-Verlag, MR1070716, ISBN 0-387-97329-X
G. H. Hardy and E. M. Wright 1978, 2000 (with general index) An Introduction to the Theory of Numbers: 5th Edition, Clarendon Press, Oxford UK, ISBN 0 19 853171 0
Lang, Serge (2004), Algebra, Graduate Texts in Mathematics 211 (4th ed.), Springer-Verlag, ISBN 0-387-95385-X
Orestein Ore 1948, 1988, Number Theory and Its History, Dover Publications, Inc. New York, ISBN 0-486-65620-9 (pbk.)

Number systems

Basic	Natural numbers $\mathbb{N}$ · Negative numbers · Integers $\mathbb{Z}$ · Rational numbers $\mathbb{Q}$ · Irrational numbers · Real numbers $\mathbb{R}$ · Imaginary numbers $\mathbb{I}\,$ · Complex numbers $\mathbb{C}$ · Algebraic numbers $\overline{\mathbb{Q}}$ · Transcendental numbers · Quaternions $\mathbb{H}$ · Octonions $\mathbb{O}$ · Sedenions $\mathbb{S}$ · Cayley–Dickson construction · Split-complex numbers $\mathbb{R}^{1,1}$

Complex extensions	Bicomplex numbers · Biquaternions · Split-quaternions · Tessarines · Hypercomplex numbers · Musean hypernumbers · Superreal numbers · Hyperreal numbers · Supernatural numbers · Surreal numbers

Other extensions	Dual numbers · Transfinite numbers · Extended real numbers · Cardinal numbers · Ordinal numbers · p-adic numbers