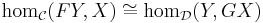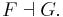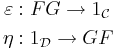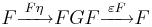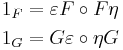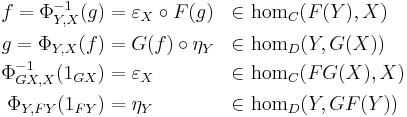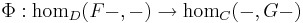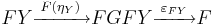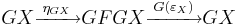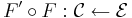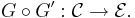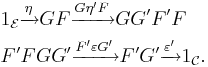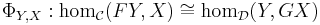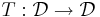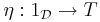Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency. It is studied in generality by the branch of mathematics known as category theory, which helps to minimize the repetition of the same logical details separately in every subject.
In the most concise symmetric definition, an adjunction between categories C and D is a pair of functors,
 and
and 
and a family of bijections
which is natural in the variables X and Y. The functor F is called a left adjoint functor, while G is called a right adjoint functor. The relationship “F is left adjoint to G” (or equivalently, “G is right adjoint to F”) is sometimes written
This definition and others are made precise below.
Contents |
Introduction
“The slogan is ‘Adjoint functors arise everywhere′.″ (Saunders Mac Lane, Categories for the working mathematician)
The long list of examples in this article is only a partial indication of how often an interesting mathematical construction is an adjoint functor. As a result, general theorems about left/right adjoint functors, such as the equivalence of their various definitions or the fact that they respectively preserve colimits/limits (which are also found in every area of math), can encode the details of many useful and otherwise non-trivial results.
Motivation
One good way to motivate adjoint functors is to vaguely explain what problem they solve, and how they solve it. (This motivation runs parallel to the definitions via universal morphisms below.)
Adjoint functors as formulaic solutions to optimization problems
It can be said an adjoint functor is a way of giving the most efficient solution to some problem via a method which is formulaic. For example, an elementary problem in ring theory is how to turn a rng (which is like a ring that might not have a multiplicative identity) into a ring. The most efficient way is to adjoin an element '1' to the rng, adjoin no unnecessary extra elements (we will need to have r+1 for each r in the ring, clearly), and impose no relations in the newly formed ring that are not forced by axioms. Moreover, this construction is formulaic in the sense that it works in essentially the same way for any rng.
This is rather vague, though suggestive, and can be made precise in the language of category theory: a construction is most efficient if it satisfies a universal property, and is formulaic if it defines a functor. Universal properties come in two types: initial properties and terminal properties. Since these are dual (opposite) notions, it is only necessary to discuss one of them.
The idea of using an initial property is to set up the problem in terms of some auxiliary category E, and then identify that what we want is to find an initial object of E. This has an advantage that the optimization — the sense that we are finding the most efficient solution — means something rigorous and is recognisable, rather like the attainment of a supremum. Picking the right category E is something of a knack: for example, take the given rng R, and make a category E whose objects are rng homomorphisms R → S, with S a ring having a multiplicative identity. The morphisms in E are commutative triangles of the form (R → S1,R → S2, S1 → S2) where S1 → S2 is a ring map (which preserves the identity). The assertion that an object R → R* is initial in E means that the ring R* is a most efficient solution to our problem.
The two facts that this method of turning rngs into rings is most efficient and formulaic can be expressed simultaneously by saying that it defines an adjoint functor.
Continuing this discussion, suppose we started with the functor F, and posed the following (vague) question: is there a problem to which F is the most efficient solution?
The notion of that F is the most efficient solution to the problem posed by G is, in a certain rigorous sense, equivalent to the notion that G poses the most difficult problem which F solves.
This has the intuitive meaning that adjoint functors should occur in pairs, and in fact they do, but this is not trivial from the universal morphism definitions. The equivalent symmetric definitions involving adjunctions and the symmetric language of adjoint functors (we can say either F is left adjoint to G or G is right ajoint to F) have the advantage of making this fact implicit.
Formal definitions
There are various definitions for adjoint functors. Their equivalence is elementary but not at all trivial and in fact highly useful. This article provides several such definitions:
- The definitions via universal morphisms are easy to state, and require minimal verifications when constructing an adjoint functor or proving two functors are adjoint. They are also the most analogous to our intuition involving optimizations.
- The definition via counit-unit adjunction is convenient for proofs about functors which are known to be adjoint, because they provide formulas that can be directly manipulated.
- The definition via hom-sets makes symmetry the most apparent, and is the reason for using the word adjoint.
Adjoint functors arise everywhere, in all areas of mathematics. Their full usefulness lies in that the structure in any of these definitions gives rise to the structures in the others via a long but trivial series of deductions. Thus, switching between them makes implicit use of a great deal of tedious details that would otherwise have to be repeated separately in every subject area. For example, naturality and terminality of the counit can be used to prove that any right adjoint functor preserve limits.
A helpful writing convention
The theory of adjoints has the terms left and right at its foundation, and there are many components which live in one of two categories C and D which are under consideration. It can therefore be extremely helpful to choose letters in alphabetical order according to whether they live in the "lefthand" category C or the "righthand" category D, and also to write them down in this order whenever possible.
In this article for example, the letters X, F, f, ε will consistently denote things which live in the category C, the letters Y, G, g, η will consistently denote things which live in the category D, and whenever possible such things will be referred to in order from left to right (a functor F:C←D can be thought of as "living" where its outputs are, in C).
Definitions via universal morphisms
A functor F : C ← D is a left adjoint functor if for each object X in C, there exists a terminal morphism from F to X. If G : C → D is another functor such that terminal morphisms to F can be taken of the form 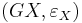 for each X (so each εX is a morphism F(GX)→X), then we say G is right adjoint to F.
for each X (so each εX is a morphism F(GX)→X), then we say G is right adjoint to F.
A functor G : C → D is a right adjoint functor if for each object Y in D, there exists an initial morphism from Y to G. If F : C ← D is another functor such that initial morphisms to G can be taken of the form 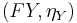 for each Y (so each ηY is a morphism Y→G(FY)), then we say F is left adjoint to F.
for each Y (so each ηY is a morphism Y→G(FY)), then we say F is left adjoint to F.
Remarks:
It is true, but not immediate from these definitions, that F is left adjoint to G if and only if G is right adjoint to F, and that every left adjoint functor is left adjoint to some right adjoint functor G which is essentially unique (and the dual statement). The equivalent symmetric definitions below make these facts less confusing to remember, and have more immediate inmplications because of the adjunction structures they invoke. On the other hand, these universal morphism definitions are useful for establishing adjoints, because they are technically minimalistic in their requirements, and intuitively meaningful in that finding universal morphisms is like optimization.
Definition via counit-unit adjunction
A counit-unit adjunction between two categories C and D consists of two functors F : C ← D and G : C → D and two natural transformations
respectively called the counit and the unit of the adjunction (terminology from universal algebra*), such that the compositions
are the identity transformations 1F and 1G on F and G respectively.
In this situation we say that F is left adjoint to G and G is right adjoint to F , and may indicate this relationship by writing 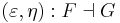 , or simply
, or simply 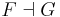 .
.
Remarks:
In equation form, the above conditions on (ε,η) are the counit-unit equations
which mean that for each X in C and each Y in D,
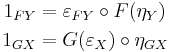 .
.
These equations are useful in reducing proofs about adjoint functors to algebraic manipulations. They are sometimes called the zig-zag equations because of the appearance of the corresponding string diagrams. A way to remember them is to first write down the nonsensical equation 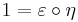 and then fill in either F or G in one of the two simple ways which make the compositions defined.
and then fill in either F or G in one of the two simple ways which make the compositions defined.
*Warning:
The use of the prefix co in counit here is not consistent with the terminology of limits and colimits, because a colimit satisfies an initial property whereas the counit morphisms will satisfy terminal properties, and dually. The term unit here is borrowed from the theory of monads where it looks like the insertion of the identity 1 into a monoid.
Definition via hom-set adjunction
A hom-set adjunction between two categories C and D consists of two functors F : C ← D and G : C → D and a natural isomorphism
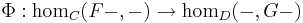 .
.
This specifies a family of bijections
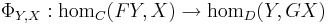 .
.
for all objects X in C and Y in D.
In this situation we say that F is left adjoint to G and G is right adjoint to F , and may indicate this relationship by writing 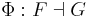 , or simply
, or simply 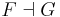 .
.
Remarks:
This definition is a logical compromise in that it is somewhat more difficult to satisfy than the universal morphism definitions, and has less immediate implications than the counit-unit definition. It is useful because of its obvious symmetry, and as a stepping-stone between the other definitions.
In order to interpret Φ as a natural isomorphism, one must recognize homC(F–, –) and homD(–, G–) as functors. In fact, they are both bifunctors from Dop × C to Set (the category of sets). For details, see the article on hom functors. Explicitly, the naturality of Φ means that for all morphisms f : X → X ′ in C and all morphisms g : Y ′ → Y in D the following diagram commutes:
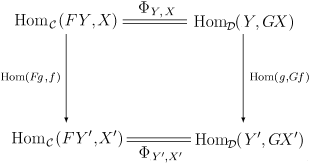
The vertical arrows in this diagram are those induced by composition with f and g.
Adjoint situations in full
The next three subsections explain the equivalence of the above definitions. There are hence numerous functors and natural transformations associated with every adjoint situation, with an intricate web of relationships among them, and in effect, one is able to construct all of this data starting with only some of the pieces. The final results of this analysis are summarized here before justifying them.
An adjoint situation between categories C and D consists of
- A functor F : C ← D called the left adjoint
- A functor G : C → D called the right adjoint
- A natural isomorphism Φ : homC(F–,–) → homD(–,G–)
- A natural transformation ε : FG → 1C called the counit
- A natural transformation η : 1D → GF called the unit
If X denotes any object of C and Y denotes any object of D, the web of relationships between these functors and transformations can be neatly summarized with a single (compound) assertion involving commutative diagrams:
For every C-morphism  there is a unique D-morphism
there is a unique D-morphism 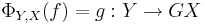 such that the diagrams below commute, and for every D-morphism
such that the diagrams below commute, and for every D-morphism 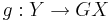 there is a unique C-morphism
there is a unique C-morphism 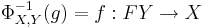 in C such that the diagrams below commute:
in C such that the diagrams below commute:
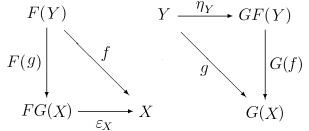
From this assertion, one can recover that:
- The transformations ε, η, and Φ are related by the equations
- The transformations ε, η satisfy the counit-unit equations
- Each pair
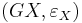 is a terminal morphism from F to X in C
is a terminal morphism from F to X in C - Each pair
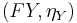 is an initial morphism from Y to G in D
is an initial morphism from Y to G in D
In particular, the equations above allow one to define (ε,η) in terms of Φ or vice versa. All of the above claims are justified in the next three subsections.
Universal morphisms induce hom-set adjunction
Given a right adjoint functor 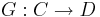 in the sense of initial morphisms, we can construct a functor
in the sense of initial morphisms, we can construct a functor  and hom-set adjunction
and hom-set adjunction
in the following steps:
- For for each Y in D, choose an initial morphism
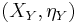 from Y to G, so we have
from Y to G, so we have 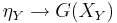 .
.
- Initiality of these morphisms allows us to construct a unique functor
 such that
such that 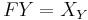 and
and 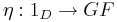 is a natural transformation.
is a natural transformation.
- For every morphism
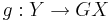 , initiality of
, initiality of 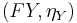 means we can let
means we can let 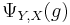 be the unique morphism
be the unique morphism  such that
such that 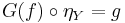 .
.
- The map
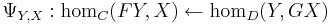 is injective by uniqueness and surjective because we can solve its defining equation for f. It is natural in X because η is natural, and natural in Y because G is a functor. Hence letting
is injective by uniqueness and surjective because we can solve its defining equation for f. It is natural in X because η is natural, and natural in Y because G is a functor. Hence letting 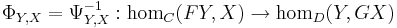 gives a hom-set adjunction as required.
gives a hom-set adjunction as required.
A similar argument allows one to construct a hom-set adjunction from the terminal morphisms to a left adjoint functor. (The construction given here of starting with a right adjoint is slightly more common, since the right adjoint in many adjoint pairs is a trivially defined inclusion or forgetful functor.)
Counit-unit adjunction induces hom-set adjunction
Given functors  ,
, 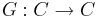 , and a counit-unit adjunction
, and a counit-unit adjunction 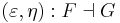 , we can construct a hom-set adjunction
, we can construct a hom-set adjunction
in the following steps:
- For each
 and each
and each 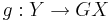 , define
, define

- The transformations Φ and Ψ are natural because η and ε are natural.
- Using, in order, that F is a functor, that ε is natural, and the counit-unit equation
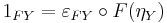 , we obtain
, we obtain
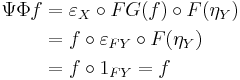
- hence ΨΦ is the identity transformation.
- Dually, using that G is a functor, that η is natural, and the counit-unit equation
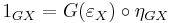 , we obtain
, we obtain
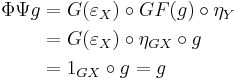
- hence ΦΨ is the identity transformation, so Φ is a natural isomorphism with inverse Φ-1 = Ψ.
Hom-set adjunction induces all of the above
Given functors  ,
, 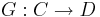 , and a hom-set adjunction
, and a hom-set adjunction 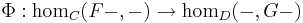 , we can construct a counit-unit adjunction
, we can construct a counit-unit adjunction
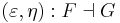 ,
,
which defines families of initial and terminal morphisms, in the following steps:
- Let
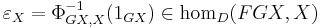 for each X in C, where
for each X in C, where 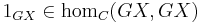 is the identity morphism.
is the identity morphism.
- Let
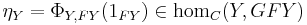 for each Y in D, where
for each Y in D, where 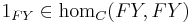 is the identity morphism.
is the identity morphism.
- The bijectivity and naturality of Φ imply that each
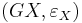 is a terminal morphism from X to F in C, and each
is a terminal morphism from X to F in C, and each 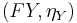 is an initial morphism from Y to G in D.
is an initial morphism from Y to G in D.
- The naturality of Φ implies the naturality of ε and η, and the two formulas
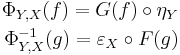
- for each f: FY → X and g: Y → GX (which completely determine Φ).
- Substituting FY for X and
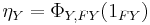 for g in the second formula gives the first counit-unit equation
for g in the second formula gives the first counit-unit equation
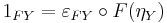 ,
,- and substituting GX for Y and
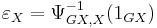 for f in the first formula gives the second counit-unit equation
for f in the first formula gives the second counit-unit equation 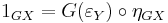 .
.
Historical perspective
Ubiquity of adjoint functors
The idea of an adjoint functor was formulated by Daniel Kan in 1958. Like many of the concepts in category theory, it was suggested by the needs of homological algebra, which was at the time devoted to computations. Those faced with giving tidy, systematic presentations of the subject would have noticed relations such as
- hom(F(X), Y) = hom(X, G(Y))
in the category of abelian groups, where F was the functor 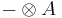 (i.e. take the tensor product with A), and G was the functor hom(A,–). The use of the equals sign is an abuse of notation; those two groups are not really identical but there is a way of identifying them that is natural. It can be seen to be natural on the basis, firstly, that these are two alternative descriptions of the bilinear mappings from X × A to Y. That is, however, something particular to the case of tensor product. What category theory teaches is that 'natural' is a well-defined term of art in mathematics: natural equivalence.
(i.e. take the tensor product with A), and G was the functor hom(A,–). The use of the equals sign is an abuse of notation; those two groups are not really identical but there is a way of identifying them that is natural. It can be seen to be natural on the basis, firstly, that these are two alternative descriptions of the bilinear mappings from X × A to Y. That is, however, something particular to the case of tensor product. What category theory teaches is that 'natural' is a well-defined term of art in mathematics: natural equivalence.
The terminology comes from the Hilbert space idea of adjoint operators T, U with <Tx,y> = <x,Uy>, which is formally similar to the above relation between hom-sets. We say that F is left adjoint to G, and G is right adjoint to F. Note that G may have itself a right adjoint that is quite different from F (see below for an example). The analogy to adjoint maps of Hilbert spaces can be made precise in certain contexts [1].
If one starts looking for these adjoint pairs of functors, they turn out to be very common in abstract algebra, and elsewhere as well. The example section below provides evidence of this; furthermore, universal constructions, which may be more familiar to some, give rise to numerous adjoint pairs of functors.
In accordance with the thinking of Saunders Mac Lane, any idea such as adjoint functors that occurs widely enough in mathematics should be studied for its own sake.
Problems formulated with adjoint functors
By itself, the generality of the adjoint functor concept is not an advantage to most mathematicians. Concepts are judged according to their use in solving problems, at least as much as for their use in building theories. The tension between these two potential motivations for developing a mathematical concept was especially great during the 1950s when category theory was initially developed. Enter Alexander Grothendieck, who used category theory to take compass bearings in foundational, axiomatic work — in functional analysis, homological algebra and finally algebraic geometry.
It is probably wrong to say that he promoted the adjoint functor concept in isolation: but recognition of the role of adjunction was inherent in Grothendieck's approach. For example, one of his major achievements was the formulation of Serre duality in relative form — one could say loosely, in a continuous family of algebraic varieties. The entire proof turned on the existence of a right adjoint to a certain functor. This is something undeniably abstract, and non-constructive, but also powerful in its own way.
The case of partial orders
Every partially ordered set can be viewed as a category (with a single morphism between x and y if and only if x ≤ y). A pair of adjoint functors between two partially ordered sets is called a Galois connection (or, if it is contravariant, an antitone Galois connection). See that article for a number of examples: the case of Galois theory of course is a leading one. Any Galois connection gives rise to closure operators and to inverse order-preserving bijections between the corresponding closed elements.
As is the case for Galois groups, the real interest lies often in refining a correspondence to a duality (i.e. antitone order isomorphism). A treatment of Galois theory along these lines by Kaplansky was influential in the recognition of the general structure here.
The partial order case collapses the adjunction definitions quite noticeably, but can provide several themes:
- adjunctions may not be dualities or isomorphisms, but are candidates for upgrading to that status
- closure operators may indicate the presence of adjunctions, as corresponding monads (cf. the Kuratowski closure axioms)
- a very general comment of Martin Hyland is that syntax and semantics are adjoint: take C to be the set of all logical theories (axiomatizations), and D the power set of the set of all mathematical structures. For a theory T in C, let F(T) be the set of all structures that satisfy the axioms T; for a set of mathematical structures S, let G(S) be the minimal axiomatization of S. We can then say that F(T) is a subset of S if and only if T logically implies G(S): the "semantics functor" F is left adjoint to the "syntax functor" G.
- division is (in general) the attempt to invert multiplication, but many examples, such as the introduction of implication in propositional logic, or the ideal quotient for division by ring ideals, can be recognised as the attempt to provide an adjoint.
Together these observations provide explanatory value all over mathematics.
Examples
Free groups (a detailed example)
In order to stay oriented when thinking of adjoint functors, it helps to keep the details of a specific adjoint situation in mind. The adjoint situation of free groups is a good example to be familiar with. Suppose that F : Grp ← Set is the functor assigning to each set Y the free group generated by the elements of Y, and that G : Grp → Set is the forgetful functor, which assigns to each group X its underlying set.
Terminal morphisms. For each group X, the group FGX is the free group generated freely by GX, the elements of X. (Think of these elements as placed in parentheses to indicate that they are independent generators.) Let 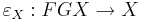 be the group homomorphism which sends the generators of FGX to the elements of X they correspond to (so this is simply the action of "dropping parentheses"). Then each
be the group homomorphism which sends the generators of FGX to the elements of X they correspond to (so this is simply the action of "dropping parentheses"). Then each  is a terminal morphism from F to X, because any group homomorphism from a free group FZ to X will factor through
is a terminal morphism from F to X, because any group homomorphism from a free group FZ to X will factor through  via a unique set map from Z to Y. This means that (F,G) is an adjoint pair.
via a unique set map from Z to Y. This means that (F,G) is an adjoint pair.
Initial morphisms. For each set Y, the set GFY is just the underlying set of the free group FY generated by Y. Let  be the set map given by "inclusion of generators". Then each
be the set map given by "inclusion of generators". Then each 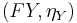 is an initial morphism from Y to G, because any set map from Y to the underlying set GW of a group will factor through
is an initial morphism from Y to G, because any set map from Y to the underlying set GW of a group will factor through  via a unique group homomorphism from FY to W. This also means that (F,G) is an adjoint pair.
via a unique group homomorphism from FY to W. This also means that (F,G) is an adjoint pair.
Hom-set adjunction. Maps from the free group FY to a group X correspond precisely to maps from the set Y to the set GX in the obvious way. One can verify directly that this correspondence is a natural transformation, which means it is a hom-set adjunction for the pair (F,G).
Counit-unit adjunction. One can also verify directly that ε and η are natural. Then, a direct verification that they form a counit-unit adjunction 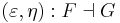 is as follows:
is as follows:
The first counit-unit equation 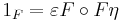 says that for each set Y the composition
says that for each set Y the composition
should be the identity. The intermediate group FGFY is the free group generated freely by the words of the free group FY. (Think of these words as placed in parentheses to indicate that they are independent generators.) The arrow  is the group homomorphism from FY into FGFY sending each generator y of FY to the corresponding word of length one (y) as a generator of FGFY. The arrow
is the group homomorphism from FY into FGFY sending each generator y of FY to the corresponding word of length one (y) as a generator of FGFY. The arrow 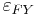 is the group homomorphism from FGFY to FY sending each generator to the word of FY it corresponds to (so this map is "dropping parentheses"). The composition of these maps is indeed the identity on FY.
is the group homomorphism from FGFY to FY sending each generator to the word of FY it corresponds to (so this map is "dropping parentheses"). The composition of these maps is indeed the identity on FY.
The second counit-unit equation 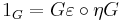 says that for each group X the composition
says that for each group X the composition
should be the identity. The intermediate set GFGX is just the underlying set of FGX. The arrow 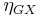 is the "inclusion of generators" set map from the set GX to the set GFGX. The arrow
is the "inclusion of generators" set map from the set GX to the set GFGX. The arrow 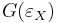 is the set map from GFGX to GX which underlies the group homomorphism sending each generator of FGX to the element of X it corresponds to ("dropping parentheses"). The composition of these maps is indeed the identity on GX.
is the set map from GFGX to GX which underlies the group homomorphism sending each generator of FGX to the element of X it corresponds to ("dropping parentheses"). The composition of these maps is indeed the identity on GX.
Free constructions and forgetful functors
Free groups, free abelian groups, free rings, free commutative rings, free modules, free vector spaces, etc., are all applications of a left adjoint to a forgetful functor which assigns to an algebraic object its underlying set. These algebraic free functors have generally the same description of as in the detailed description of the free group situation above.
Diagonal functors and limits
Products, fibred products, equalizers, and kernels are all examples of the categorical notion of a limit. Any limit functor is right adjoint to a corresponding diagonal functor (provided the category has the type of limits in question), and the the counit of the adjunction provides the defining maps from the limit object. Below are some specific examples.
- Products Let Π : Grp2 → Grp the functor which assigns to each pair (X1, X2) the product group X1×X2, and let Δ : Grp2 ← Grp be the diagonal functor which assigns to every group X the pair (X, X) in the product category Grp2. The universal property of the product group shows that Π is right-adjoint to Δ. The counit of this adjunction is the defining pair of projection maps from X1×X2 to X1 and X2 which define the limit, and the unit is the diagonal inclusion of a group X into X1×X2 (mapping x to (x,x)).
- The cartesian product of sets, the product of rings, the product of topological spaces etc. follow the same pattern; it can also be extended in a straightforward manner to more than just two factors. More generally, any type of limit is right adjoint to a diagonal functor.
- Kernels. Consider the category D of homomorphisms of abelian groups. If f1 : A1 → B1 and f2 : A2 → B2 are two objects of D, then a morphism from f1 to f2 is a pair (gA, gB) of morphisms such that gBf1 = f2gA. Let G : D → Ab be the functor which assigns to each homomorphism its kernel and let F : D ← Ab' be the functor which maps the group A to the homomorphism A → 0. Then G is right adjoint to F, which expresses the universal property of kernels. The counit of this adjunction is the defining embedding of a homomorphism's kernel into the homomorphism's domain, and the unit is the morphism identifying a group A with the kernel of the homomorphism A → 0.
- A suitable variation of this example also shows that the kernel functors for vector spaces and for modules are right adjoints. Analogously, one can show that the cokernel functors for abelian groups, vector spaces and modules are left adjoints.
Colimits and diagonal functors
Coproducts, fibred coproducts, coequalizers, and cokernels are all examples of the categorical notion of a colimit. Any colimit functor is left adjoint to a corresponding diagonal functor (provided the category has the type of colimits in question), and the the unit of the adjunction provides the defining maps into the colimit object. Below are some specific examples.
- Coproducts. If F : Ab ← Ab2 assigns to every pair (X1, X2) of abelian groups their direct sum, and if G : Ab → Ab2 is the functor which assigns to every abelian group Y the pair (Y, Y), then F is left adjoint to G, again a consequence of the universal property of direct sums. The unit of this adjoint pair is the defining pair of inclusion maps from X1 and X2 into the direct sum, and the counit is the additive map from the direct sum of (X,X) to back to X (sending an element (a,b) of the direct sum to the element a+b of X).
- Analogous examples are given by the direct sum of vector spaces and modules, by the free product of groups and by the disjoint union of sets.
Further examples
In algebra
- Adjoining an identity to a rng. This example was discussed in the motivation section above. Given a rng R, a multiplicative identity element can be added by taking RxZ and defining a Z-bilinear product with (r,0)(0,1) = (0,1)(r,0) = (r,0), (r,0)(s,0) = (rs,0), (0,1)(0,1) = (0,1). This constructs a left adjoint to the functor taking a ring to the underlying rng.
- Ring extensions. Suppose R and S are rings, and ρ : R → S is a ring homomorphism. Then S can be seen as a (left) R-module, and the tensor product with S yields a functor F : R-Mod → S-Mod. Then F is left adjoint to the forgetful functor G : S-Mod → R-Mod.
- Tensor products. If R is a ring and M is a right R module, then the tensor product with M yields a functor F : R-Mod → Ab. The functor G : Ab → R-Mod, defined by G(A) = homZ(M,A) for every abelian group A, is a right adjoint to F.
- From monoids and groups to rings The integral monoid ring construction gives a functor from monoids to rings. This functor is left adjoint to the functor that associates to a given ring its underlying multiplicative monoid. Similarly, the integral group ring construction yields a functor from groups to rings, left adjoint to the functor that assigns to a given ring its group of units. One can also start with a field K and consider the category of K-algebras instead of the category of rings, to get the monoid and group rings over K.
- Field of fractions. Consider the category Domm of integral domains with injective morphisms. The forgetful functor Field → Domm from fields has a left adjoint - it assigns to every integral domain its field of fractions.
- Polynomial rings. Let Ring* be the category of pointed commutative rings with unity (pairs (A,a) where A is a ring,
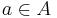 and morphisms preserve the distinguished elements). The forgetful functor G:Ring* → Ring has a left adjoint - it assigns to every ring R the pair (R[x],x) where R[x] is the polynomial ring with coefficients from R.
and morphisms preserve the distinguished elements). The forgetful functor G:Ring* → Ring has a left adjoint - it assigns to every ring R the pair (R[x],x) where R[x] is the polynomial ring with coefficients from R.
- Abelianization. Consider the inclusion functor G : Ab → Grp from the category of abelian groups to category of groups. It has a left adjoint called abelianization which assigns to every group G the quotient group Gab=G/[G,G].
- The Grothendieck group. In K-theory, the point of departure is to observe that the category of vector bundles on a topological space has a commutative monoid structure under direct sum. One may make an abelian group out of this monoid, the Grothendieck group, by formally adding an additive inverse for each bundle (or equivalence class). Alternatively one can observe that the functor that for each group takes the underlying monoid (ignoring inverses) has a left adjoint. This is a once-for-all construction, in line with the third section discussion above. That is, one can imitate the construction of negative numbers; but there is the other option of an existence theorem. For the case of finitary algebraic structures, the existence by itself can be referred to universal algebra, or model theory; naturally there is also a proof adapted to category theory, too.
- Frobenius reciprocity in the representation theory of groups: see induced representation. This example foreshadowed the general theory by about half a century.
In topology
- A functor with a left and a right adjoint. Let G be the functor from topological spaces to sets that associates to every topological space its underlying set (forgetting the topology, that is). G has a left adjoint F, creating the discrete space on a set Y, and a right adjoint H creating the trivial topology on Y.
- Suspensions and loop spaces Given topological spaces X and Y, the space [SX, Y] of homotopy classes of maps from the suspension SX of X to Y is naturally isomorphic to the space [X, ΩY] of homotopy classes of maps from X to the loop space ΩY of Y. This is an important fact in homotopy theory.
- Stone-Čech compactification. Let KHaus be the category of compact Hausdorff spaces and G : KHaus → Top be the forgetful functor to the category of topological spaces. Then G has a left adjoint F : Top → KHaus, the Stone–Čech compactification. The counit of this adjoint pair yields a continuous map from every topological space X into its Stone-Čech compactification. This map is an embedding (i.e. injective, continuous and open) if and only if X is a Tychonoff space.
- Direct and inverse images of sheaves Every continuous map f : X → Y between topological spaces induces a functor f ∗ from the category of sheaves (of sets, or abelian groups, or rings...) on X to the corresponding category of sheaves on Y, the direct image functor. It also induces a functor f −1 from the category of sheaves of abelian groups on Y to the category of sheaves of abelian groups on X, the inverse image functor. f −1 is left adjoint to f ∗. Here a more subtle point is that the left adjoint for coherent sheaves will differ from that for sheaves (of sets).
- Soberification. The article on Stone duality describes an adjunction between the category of topological spaces and the category of sober spaces that is known as soberification. Notably, the article also contains a detailed description of another adjunction that prepares the way for the famous duality of sober spaces and spatial locales, exploited in pointless topology.
In category theory
- A series of adjunctions. The functor π0 which assigns to a category its sets of connected components is left-adjoint to the functor D which assigns to a set the discrete category on that set. Moreover, D is left-adjoint to the object functor U which assigns to each category its set of objects, and finally U is left-adjoint to A which assigns to each set the antidiscrete category on that set.
- Exponential object. In a cartesian closed category the endofunctor C → C given by –×A has a right adjoint –A.
Properties
Uniqueness of adjoints
If the functor F : C ← D has two right adjoints G and G′, then G and G′ are naturally isomorphic. The same is true for left adjoints.
Conversely, if F is left adjoint to G, and G is naturally isomorphic to G′ then F is also left adjoint to G′. More generally, if 〈F, G, ε, η〉 is an adjunction (with counit-unit (ε,η)) and
- σ : F → F′
- τ : G → G′
are natural isomorphisms then 〈F′, G′, ε′, η′〉 is an adjunction where
Here  denotes vertical composition of natural transformations, and
denotes vertical composition of natural transformations, and  denotes horizontal composition.
denotes horizontal composition.
Composition
Adjunctions can be composed in a natural fashion. Specifically, if 〈F, G, ε, η〉 is an adjunction between C and D and 〈F′, G′, ε′, η′〉 is an adjunction between D and E then the functor
is left adjoint to
The counit and the unit of this adjunction are given by the compositions:
One can then form a category whose objects are all small categories and whose morphisms are adjunctions.
Adjoints preserve limits
The most important property of adjoints is their continuity: every functor that has a left adjoint (and therefore is a right adjoint) is continuous (i.e. commutes with limits in the category theoretical sense); every functor that has a right adjoint (and therefore is a left adjoint) is cocontinuous (i.e. commutes with colimits).
Since many common constructions in mathematics are limits or colimits, this provides a wealth of information. For example:
- applying a right adjoint functor to a product of objects yields the product of the images;
- applying a left adjoint functor to a coproduct of objects yields the coproduct of the images;
- every right adjoint functor is left exact;
- every left adjoint functor is right exact.
Additivity
If C and D are preadditive categories and F : C ← D is an additive functor with a right adjoint G : C → D, then G is also an additive functor and the hom-set bijections
are, in fact, isomorphisms of abelian groups. Dually, if G is additive with a left adjoint F, then F is also additive.
Moreover, if both C and D are additive categories (i.e. preadditive categories with all finite biproducts), then any pair of adjoint functors between them are automatically additive.
General existence theorem
Not every functor G : C → D admits a left adjoint. If C is a complete category, then the functors with left adjoints can be characterized by the adjoint functor theorem of Peter J. Freyd: G has a left adjoint if and only if it is continuous and a certain smallness condition is satisfied: for every object Y of D there exists a family of morphisms
- fi : Y → G(Xi)
where the indices i come from a set I, not a proper class, such that every morphism
- h : Y → G(X)
can be written as
- h = G(t) o fi
for some i in I and some morphism
- t : Xi → X in C.
An analogous statement characterizes those functors with a right adjoint.
Relationship to other categorical concepts
Universal constructions
As stated earlier, an adjunction between categories C and D gives rise to a family of universal morphisms, one for each object in C and one for each object in D. Conversely, if there exists a universal morphism to a functor G : C → D from every object of D, then G has a left adjoint.
However, universal constructions are more general than adjoint functors: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of D (equivalently, every object of C).
Equivalences of categories
Every equivalence of categories defines an adjunction. If F : C ← D and G : C → D are functors with natural isomorphisms ε : FG → 1C and η : 1D → GF then (F, G) form an adjoint pair with counit ε and unit η. Conversely, an adjunction 〈F, G, ε, η〉 defines an equivalence of categories if and only if the counit and unit are natural isomorphisms (and not just natural transformations).
If (F, G) define an equivalence of categories, then F is not only a left adjoint of G but a right adjoint as well. Explicitly, if 〈F, G, ε, η〉 is an adjoint equivalence then so is 〈G, F, η−1, ε−1〉.
Every adjunction 〈F, G, ε, η〉 extends an equivalence of certain subcategories. Define C1 as the full subcategory of C consisting of those objects X of C for which εX is an isomorphism, and define D1 as the full subcategory of D consisting of those objects Y of D for which ηY is an isomorphism. Then F and G can be restricted to D1 and C1 and yield inverse equivalences of these subcategories.
In a sense, then, adjoints are "generalized" inverses. Note however that a right inverse of F (i.e. a functor G such that FG is naturally isomorphic to 1D) need not be a right (or left) adjoint of F. Adjoints generalize two-sided inverses.
Monads
Every adjunction 〈F, G, ε, η〉 gives rise to an associated monad 〈T, η, μ〉 in the category D. The functor
is given by T = GF. The unit of the monad
is just the unit η of the adjunction and the multiplication transformation
is given by μ = GεF. Dually, the triple 〈FG, ε, FηG〉 defines a comonad in D.
Every monad arises from some adjunction—in fact, typically from many adjunctions—in the above fashion. Two constructions, called the category of Eilenberg-Moore algebras and the Kleisli category are two extremal solutions to the problem of constructing an adjunction that gives rise to a given monad.
References
- Adámek, Jiří; Horst Herrlich, and George E. Strecker (1990). Abstract and Concrete Categories. John Wiley & Sons. ISBN 0-471-60922-6. http://katmat.math.uni-bremen.de/acc/acc.pdf.
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics 5 ((2nd ed.) ed.). Springer-Verlag. ISBN 0-387-98403-8.
External links
- Adjunctions Seven short lectures on adjunctions.